Visual Proofs

 

6.1 INTRODUCTION

Figure 1. This is a famous visual proof that \(65 / 2=63 / 2\). A triangle of area \(65 / 2\) is cut into smaller pieces. After rearranging the pieces and only translating them, we get the same triangle with one square less.

6.1.1 The Power of Visual Proofs

Visual pictures are a great help for "seeing" why something is true. Some of the most beautiful proofs in mathematics can be seen to be true as such. Visual arguments also can be wrong and this is not only confined to geometric pictures. Especially when proving results in higher dimensions, where intuition from smaller dimensions come in, we can get into trouble.

Figure 2. Intersect the angle bisector at \(C\) with the perpendicular bisector of \(AB\)..

Figure 3. Triangles \(MQC\), \(MRC\) are congruent. Triangles \(MPB\), \(MPA\) too.

Figure 4. So are \({MBA}\) and \({AMR}\). Because \({AR}={BQ}\) and \({CQ}={RC}\) we have \({AC}={BC}\).

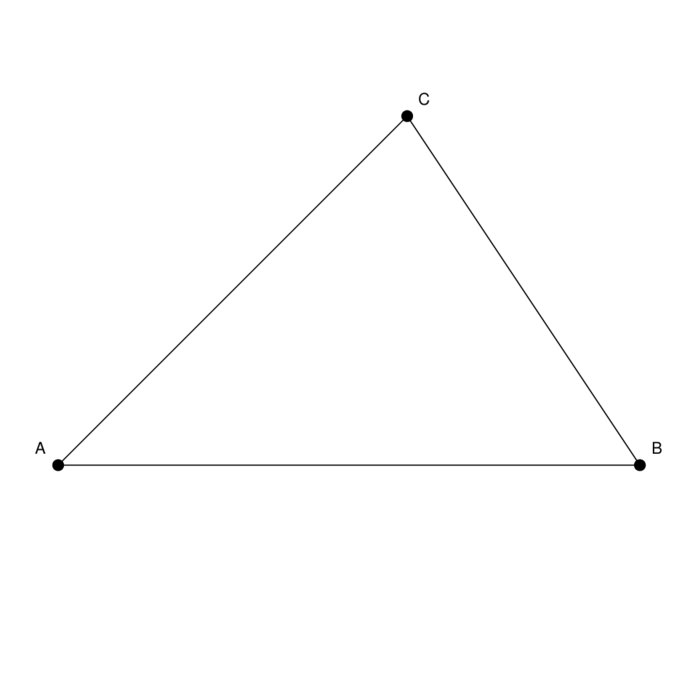
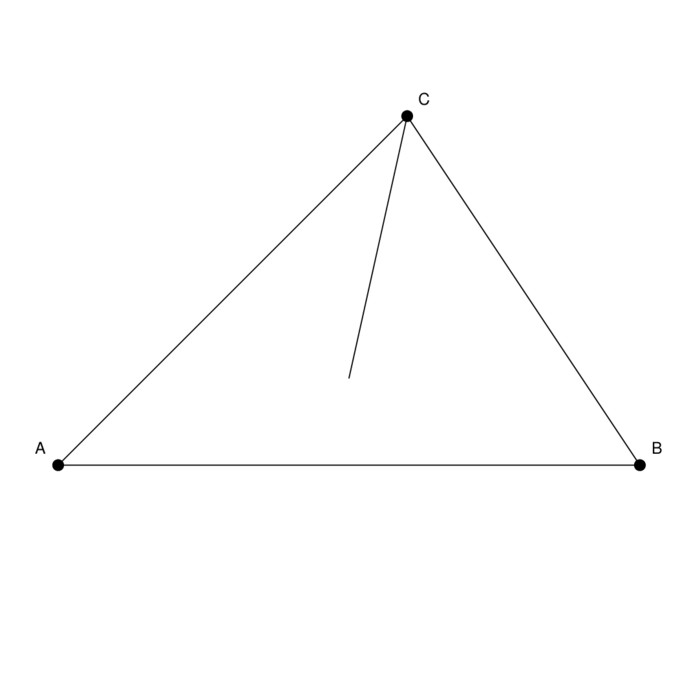
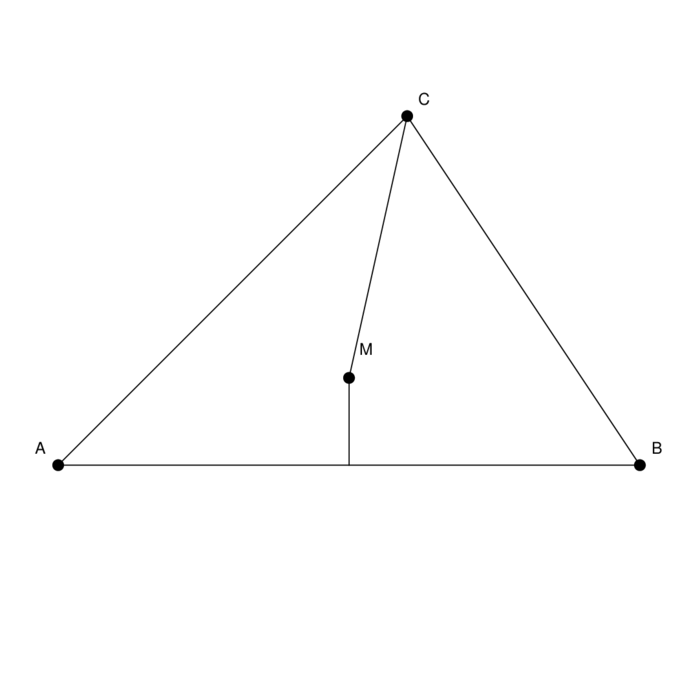
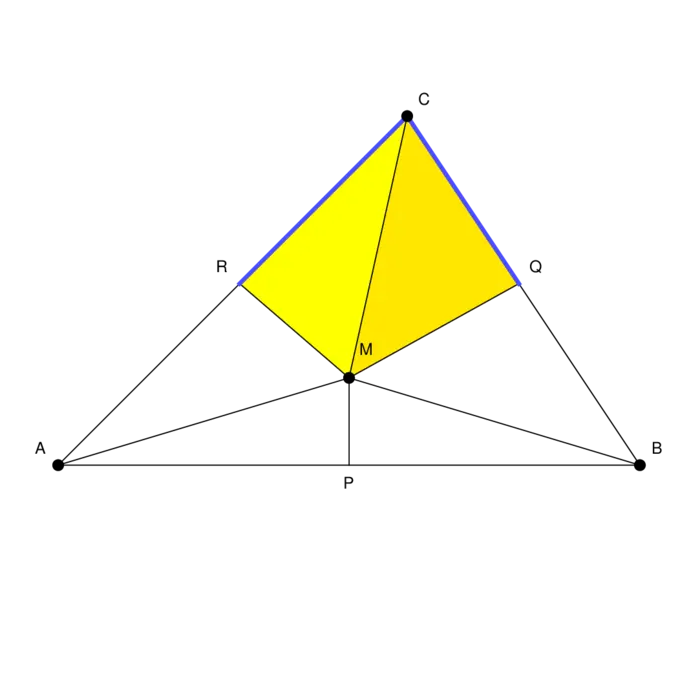
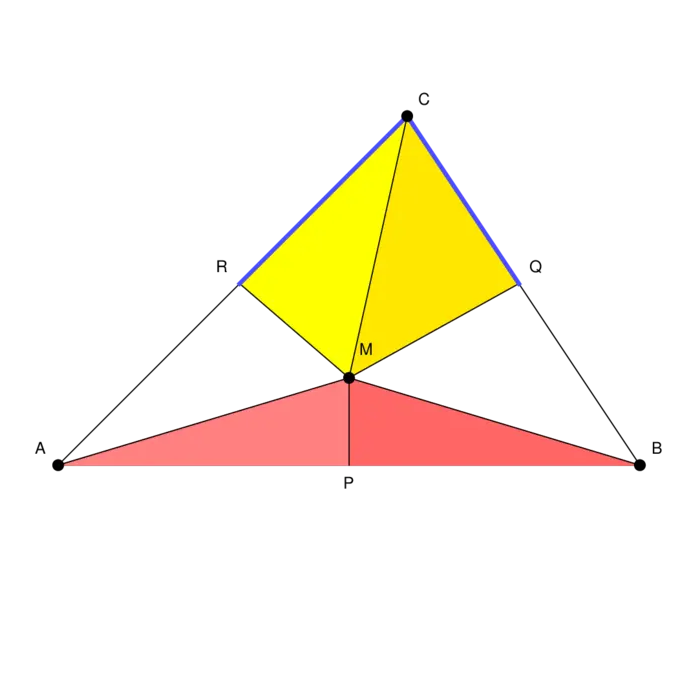
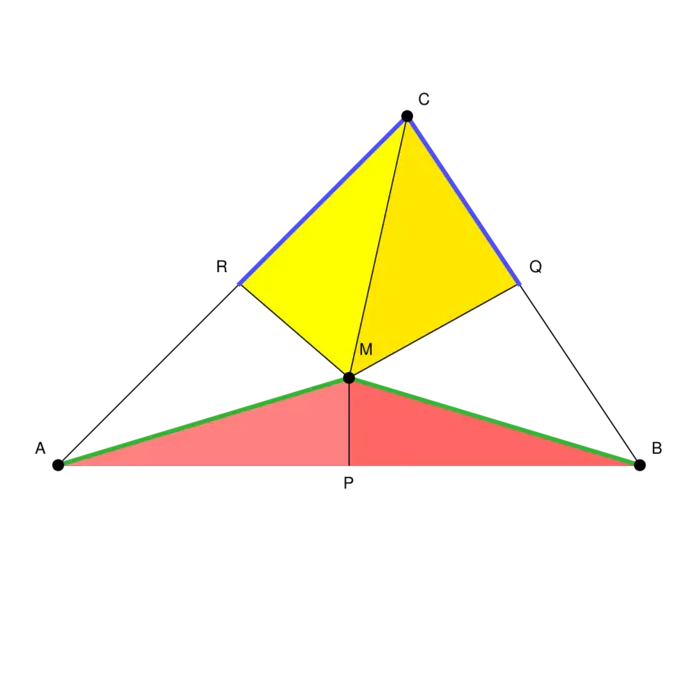
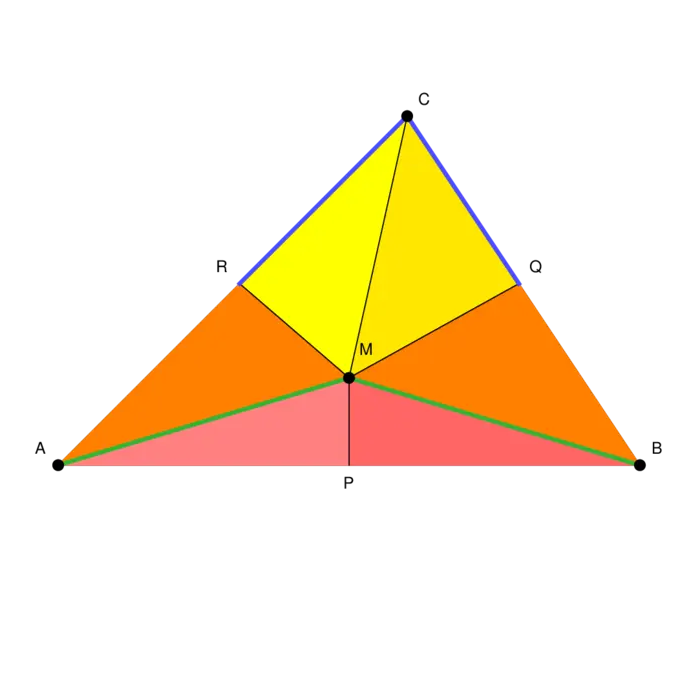
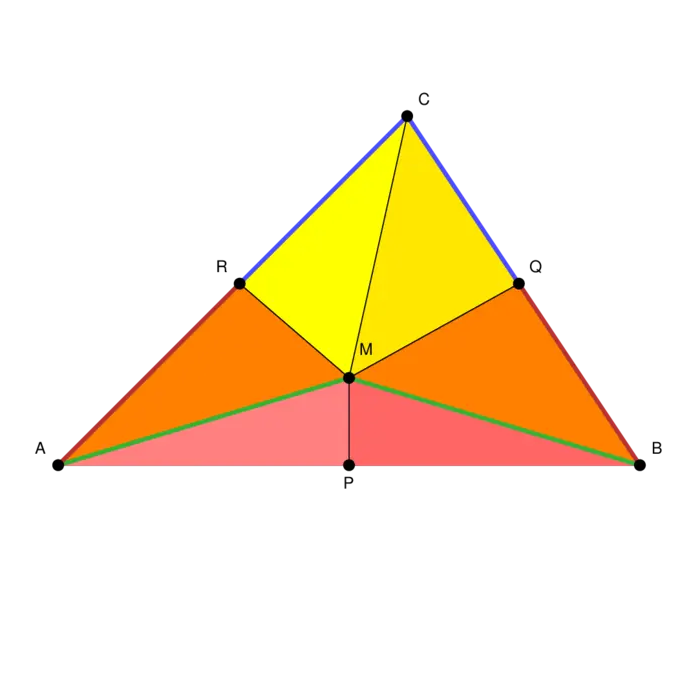
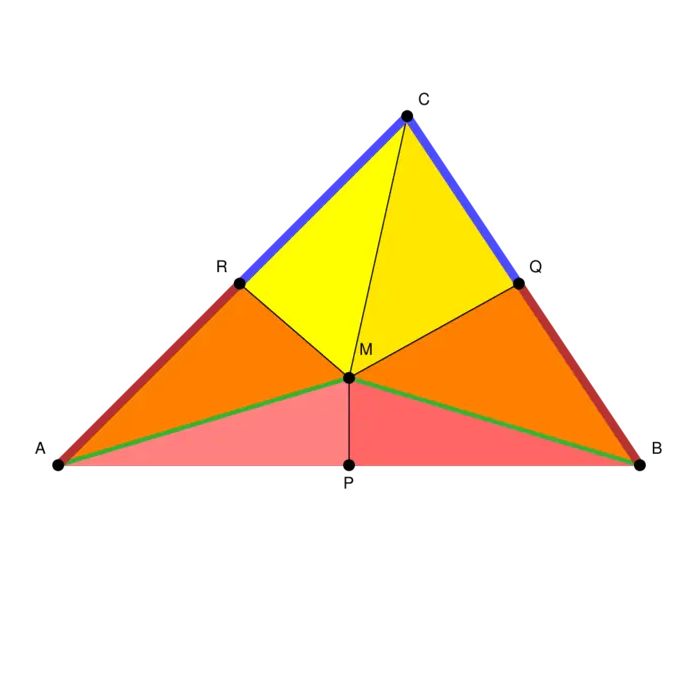
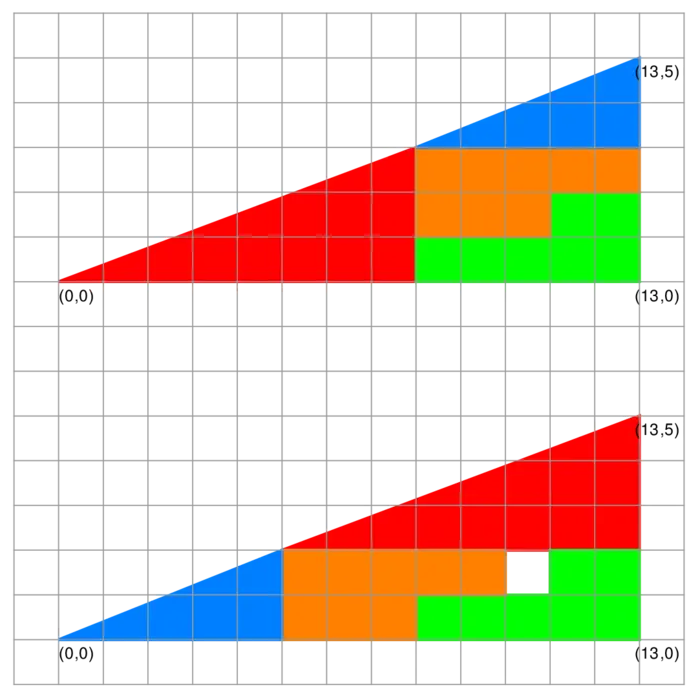
A proof that all triangles are isoscele. There is no mistake in the argument. All given steps are correct. Still, there is something wrong.

6.2 SEMINAR

6.2.1 Squares and Areas

Geometric intuition and pictures allow to prove results visually. An example:

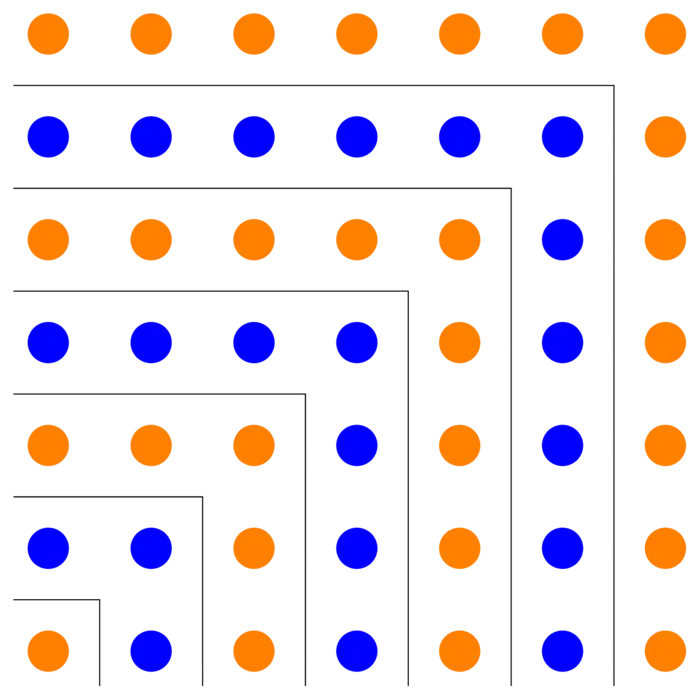
Figure 5. This is a proof without words.

1

Problem A: What formula does the above figure prove?

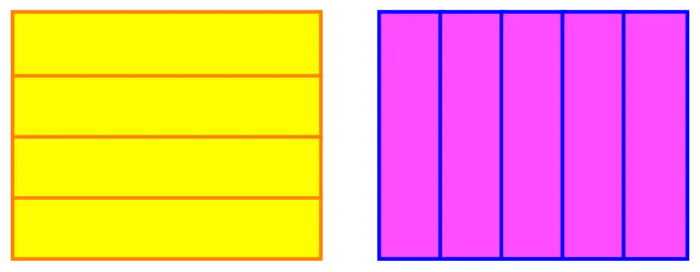
6.2.2 Commutativity in Geometry

By drawing a rectangle of side length \(a\) and \(b\), we can see that the area \(a * b\) is the same as the area \(b * a\). For the cross product or matrices, this is wrong.

Figure 6. A Cuisenaire proof that \(4 * 5=5 * 4\). Four yellow sticks of length \(5\) have the same area than \(5\) purple sticks of length \(4\).

6.2.3 Visual Proof of Pythagoras’ Theorem

Pictures help to get intuition about a mathematical result. The Pythagorean theorem was first proven geometrically. The visual proof we look at here could well have been the first which was found.

Figure 7. A visual proof of the Pythagorean theorem. It is probably one of the first proofs.

Problem B: Use Figure (6.5) for a proof of the Pythagorean theorem. You can either describe in words, or label some parts of the picture. Remember that we want to show \(c^{2}=a^{2}+b^{2}\).

6.2.4 Inequality Through Geometry

The geometric-algebraic inequality assures that the geometric mean is smaller or equal than the algebraic mean. In order to appreciate that proof, we have first to verify an identity relating the lengths \(a, b\) cut by the altitude line and height \(h\).

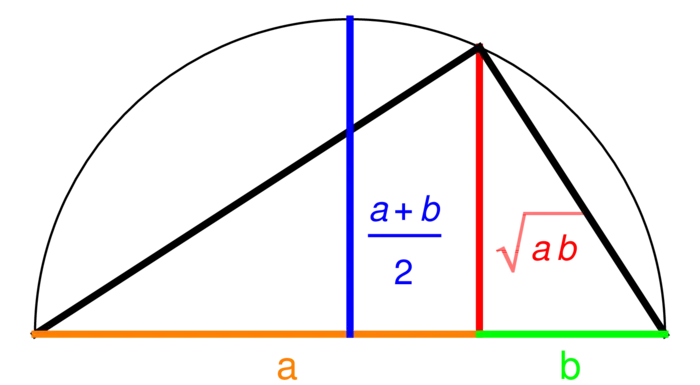
Figure 8. A visual proof of \(\sqrt{a b} \leq(a+b) / 2\).

2

Problem C: First check why the triangle in Figure (6.6) is a right angle. Then use Pythagoras three times to prove \(a b=h^{2}\). Finally check the geometric-algebraic inequality.

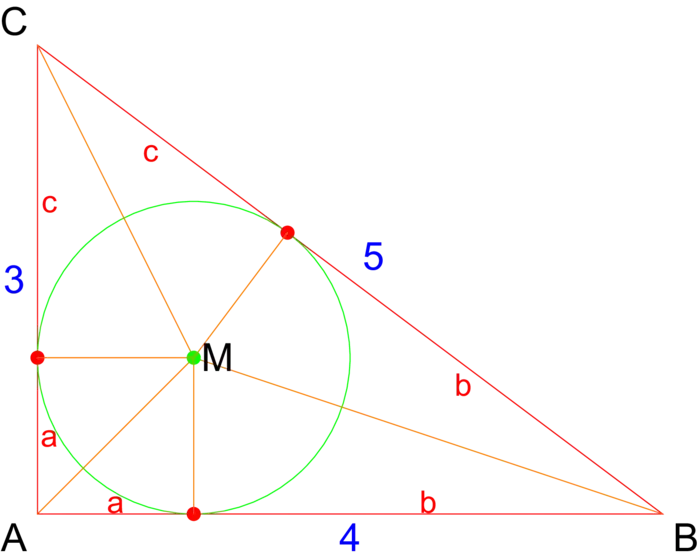
6.2.5 The Inradius of a Right Triangle

Theorem 1. The radius of the inscribed circle in a \(3: 4: 5\) triangle is \(1\).

Problem D: Use Figure (6.7) from the "9 Chapters" to prove the theorem.

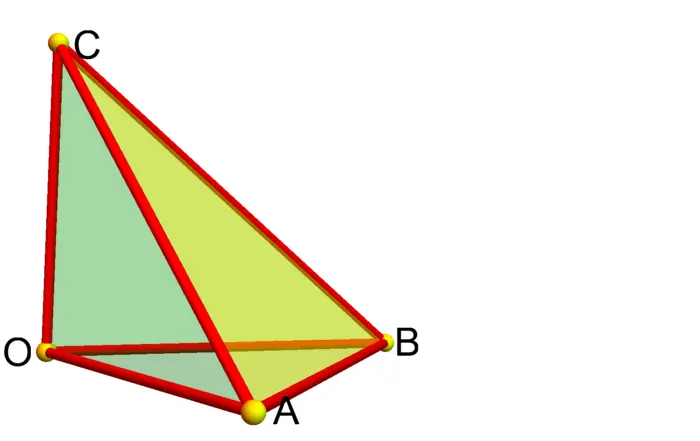
Figure 9. The \(3\)-\(4\)-\(5\) triangle. Can you use the picture to prove that \({a}=1\)?

6.2.6 Tetrahedron Volume

Find the formula for the volume of a tetrahedron given by \(4\) points \(A, B, C, D\).3

Problem E: Use Figure (6.8) to prove that the volume is a sixth of the volume of the corresponding parallelepiped.

Figure 10. The tetrahedron volume is \(1 / 6\) of a parallelepiped volume. Not only the Egyptians knew it, this figure can also be found in the "nine chapters". We build a statue which can be 3D printed.

EXERCISES

Exercise 1. The 3D Pythagoras theorem states that the square of the area of \(A B C\) is the sum of the squares of the areas of the triangles \(O A B\), \(O B C\) and \(O C A\) (which are each half of a rectangle). Use Figure (6.9) with \(A=(a, 0,0)\), \(B=(0, b, 0)\), \(C=(0,0, c)\) to verify this theorem. Use the cross product to get the areas.

Figure 11. The 3D Pythagoras theorem.

Exercise 2.

  1. Draw a picture with a planar figure explaining \((a+b)^{2}=a^{2}+2 a b+b^{2}\).
  2. Draw a picture with a 3D figure explaining \((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\).

Exercise 3. Find distance formulas which do not use any trig functions:

  1. For the distance of a point \(P\) to a line through two points \(A, B\).
  2. For the distance of a point \(P\) to a plane through three points \(A, B, C\).
  3. For the distance between the line through \(A, B\) and the line through \(C, D\).

Exercise 4. Design a visual proof for the Faulhaber formula \[1^{3}+2^{3}+3^{3}+\cdots+n^{3}=(1+2+3+\cdots+n)^{2}\] which is also called the Nichomachus theorem.

Exercise 5. Look up the rules for quaternion multiplication \(\left(u_{0}, u_{1}, u_{2}, u_{3}\right) \star\left(v_{0}, v_{1}, v_{2}, v_{3}\right)\) and verify that \(\left(0, v_{1}, v_{2}, v_{3}\right) *\left(0, w_{1}, w_{2}, w_{3}\right)=\) \((-v \cdot w, v \times w)\). Historically, this is an important identity as the dot and cross product have been introduced together in the form of quaternions.

  1. Cover of the book "Proofs without words"↩︎
  2. C. Gallant, Mathematics Magazine, 50(2), 1977, page 98↩︎
  3. "Illustrating Mathematics using 3D printers", by O. Knill and E. Slavkovsky.↩︎