Surfaces

5.1 INTRODUCTION

5.1.1 Understanding Surfaces

Surfaces are co-dimension one objects in a space. They are important because they can divide up space. We can confine water in a bottle. This is not possible for co-dimension two. You can not confine water in a curve. Similarly, if you lived in \(4\)-dimensional space, you could not store water in a two-dimensional surface. But things can get tricky already in three dimensions. There are two-dimensional closed surfaces which do not confine any space. Try to drink from a Klein bottle!

5.1.2 Describing Surfaces

A surface can mathematically be described in two fundamentally different ways. It is either given as a level surface of a function on that space. Or then it can be the image of a map called parametrization. You know this from the earth, which is a sphere. We can either say that a sphere is the set of points which have a fixed
distance to its center point. Or then we can parametrize the sphere, for example using longitude and latitude. A plane through the \(0\) can be given either as the kernel \(\left\{x \in \mathbb{R}^{3} \mid A x=0\right\}\) of a \(1 \times 3\) matrix \(A\) or then as the image \(\left\{A x \mid x \in \mathbb{R}^{2}\right\}\) of a \(3 \times 2\) matrix. The first writes \(a x+b y+c z=0\). The second writes the plane as \(v s+w t\), where \(v\), \(w\) are the column vectors of \(A\) and \(x=[s, t]^{T}\) gives the parameters.

5.2 LECTURE

5.2.1 Linear Manifolds and Spaces

If \(A\) is a matrix, the solution space of a system of equations \(A \mathbf{x}=b\) is called a linear manifold. It is the set of solutions of \(A \mathbf{x}=0\) translated so that it passes through one of the points. The equation \(3 x+2 y=6\) for example describes a line in \(\mathbb{R}^{2}\) passing through \((2,0)\) and \((0,3)\). The solutions to \(A x=0\) form a linear space, meaning that we can add or scale solutions and still have again solutions. We can rephrase the just said in that a linear space is a linear manifold which contains \(0\) . For example, for \(x+2 y+3 z=6\) we get a plane which is parallel to the plane \(x+2 y+3 z=0\). The former is a linear manifold (also called affine space), the later is a linear space. It is the solution space to \(A \mathbf{x}=0\) with \(A=[1, 2, 3]\) and \(\mathbf{x}=[x, y, z]^{T}\). Both planes are perpendicular to \(n=[1,2,3]^{T}\). To find an equation for the plane through \(3\) points \(P, Q, R\), define \(n=P Q \times P R=[a, b, c]^{T}\) then write down \(a x+b y+c z=d\), where \(d\) is obtained by plugging in a point. The cross product comes handy.

5.2.2 Normal Vectors and Planes

The following important example deals with \(A=\left[a_{1}, \ldots, a_{m}\right]\) in \(M(1, m)\).

In three dimensions, this means that the plane \(a x+b y+c z=d\) has a normal vector \(A^{T}=n=[a, b, c]^{T}\). Keep this in mind, especially because \(\mathbb{R}^{3}\) is our home.

5.2.3 Kernels and Images of Matrices

This duality result will later will identified as a fundamental theorem of linear algebra. It will be important in data fitting for example. The kernel of a matrix \(A\) is the linear space of all solution \(A x=0\). The kernel consists of all roots of \(A\). The image of a matrix \(A\) is the linear space of all vectors \(\{A x\}\). We abbreviate \(\operatorname{ker}(A)\) for the kernel and \(\operatorname{im}(A)\) of the image. We will come back to this later.

5.2.4 Exploring Non-Linear Surfaces

Given a function \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\), the solution set \(\left\{f\left(x_{1}, \ldots, x_{n}\right)=d\right\}\) is a hyper surface. We often say "surface" even so "surface" is reserved to \(n=3\). The simplest non-linear surfaces are quadratic manifolds \[x \cdot B x+A x=d\] defined by a symmetric matrix \(B\) and a row vector \(A\) and a scalar \(d\). We assume that \(B\) is not the zero matrix or else, we are in the case of a linear manifold. We also can assume \(B\) to be symmetric \(B=B^{T}\). For notation, we write \[\operatorname{Diag}(a, b, c) = \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c\end{bmatrix}\] and \(1=\operatorname{Diag}(1,1,1)\).

5.2.5 Ellipsoids

For \(B=1\) and \(A=0\) and \(d=1\) we get the sphere \(|x|^{2}=1\). In \(\mathbb{R}^{2}\), a sphere is a circle \(x^{2}+y^{2}=1\). In three dimensions we have the familiar sphere \(x^{2}+y^{2}+z^{2}=1\). An more general ellipsoid with \(B=\operatorname{Diag}\left(1 / a^{2}, 1 / b^{2}, 1 / c^{2}\right)\) is \(x^{2} / a^{2}+y^{2} / b^{2}+z^{2} / c^{2}=1\). By intersecting with \(x=0\) or \(y=0\) or \(z=0\), we see traces, which are all ellipses.

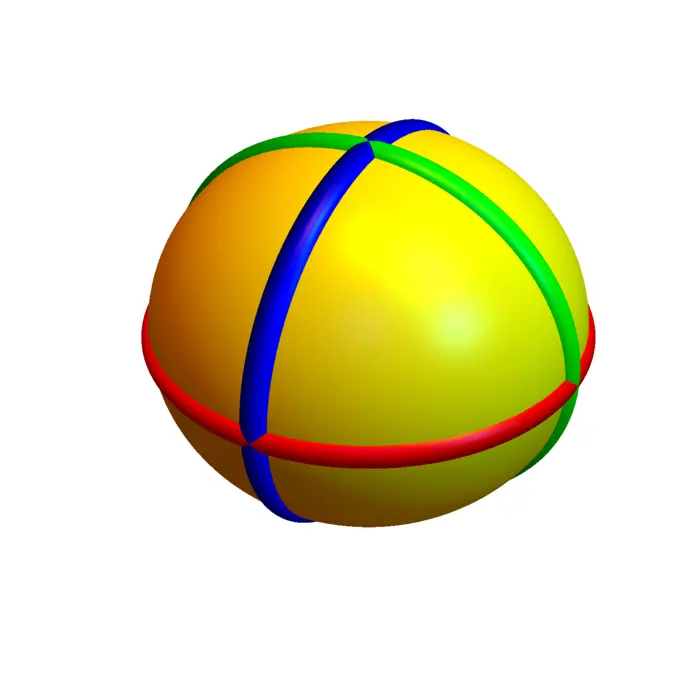
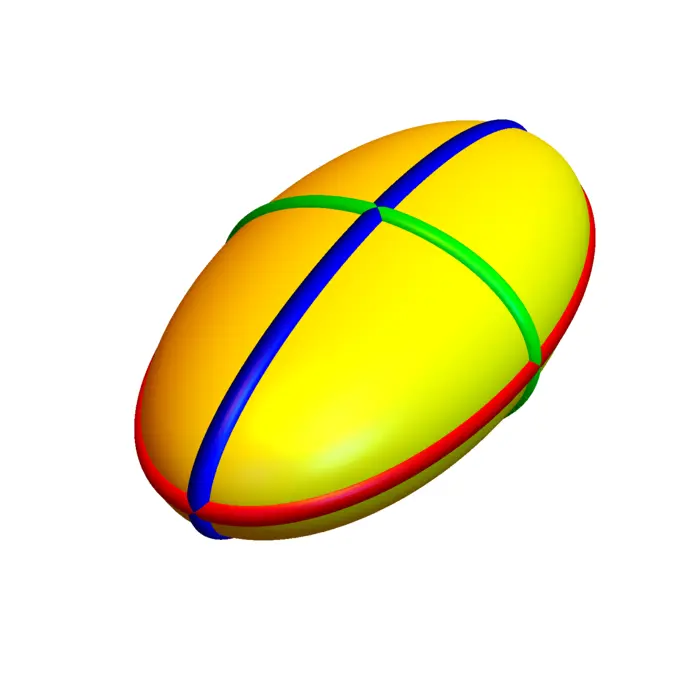
5.2.6 Hyperboloids

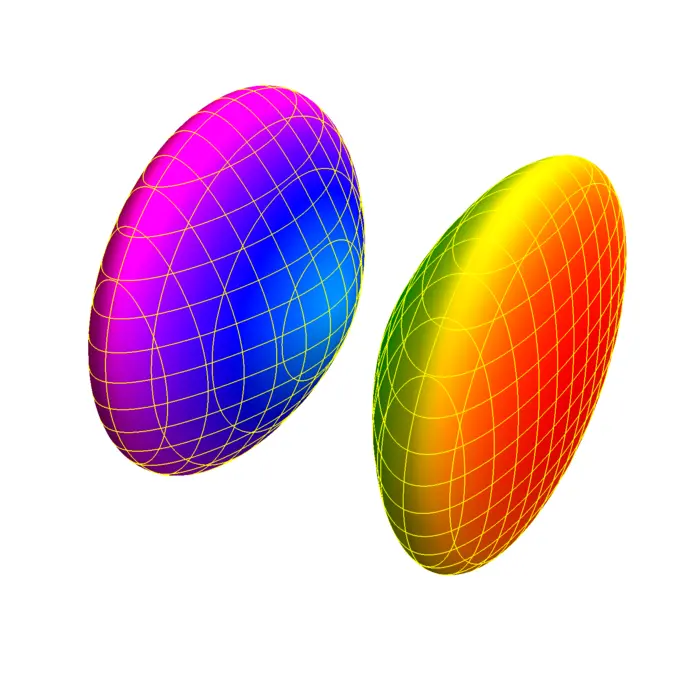
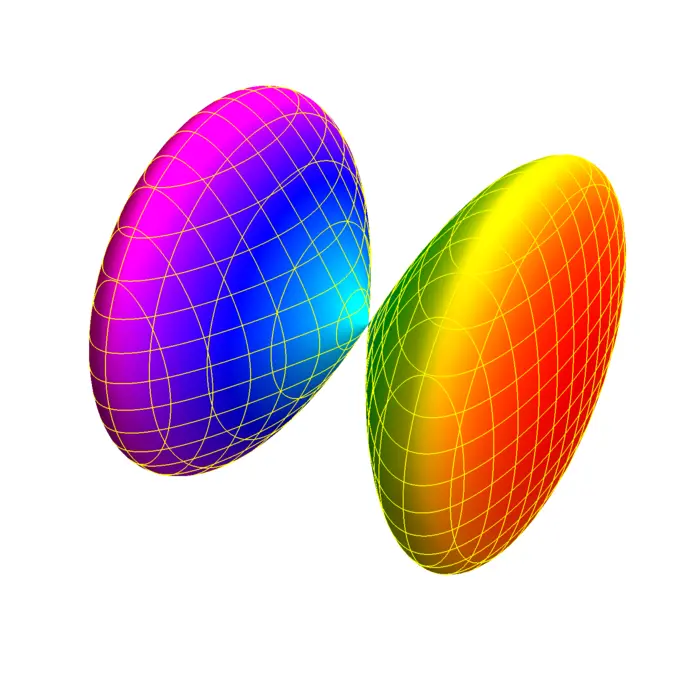
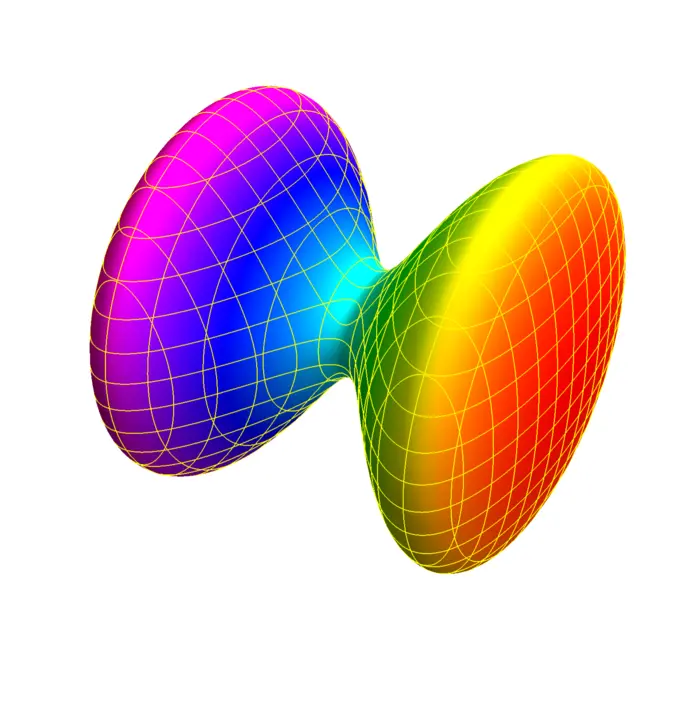
For \(B=\operatorname{Diag}(1,1,-1)\) and \(d=1\), we get a one-sheeted hyperboloid \(x^{2}+y^{2}-z^{2}=1\). For \(B=\operatorname{Diag}(1,1,-1)\) and \(d=-1\), we get a two-sheeted hyperboloid \(x^{2}+y^{2}-z^{2}=-1\). A more general hyperboloid is of the form \(x^{2} / a^{2}+y^{2} / b^{2}-z^{2} / c^{2}=d\) with \(d \neq 0\). The intersection with \(z=0\) gives in the one-sheeted case a circle, in the two-sheeted case nothing. The \(x=0\) trace or the \(y=0\) trace are both hyperbola.

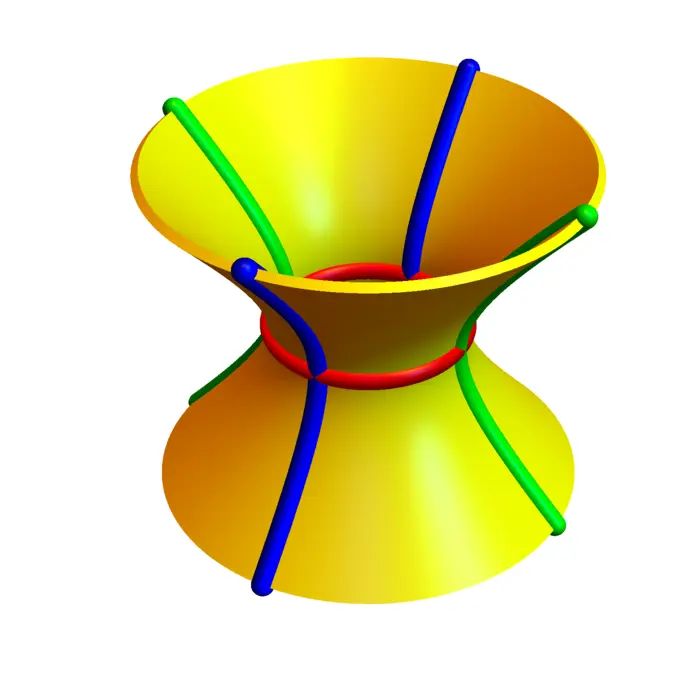
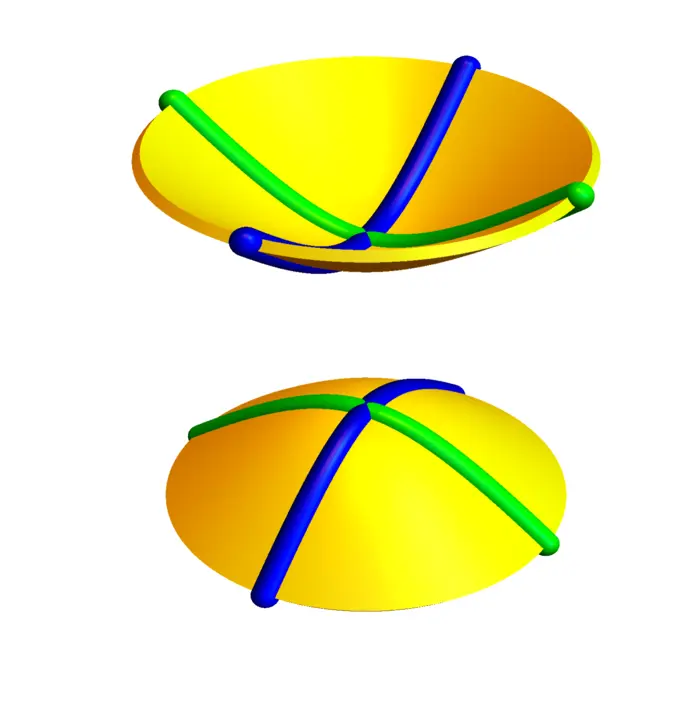
5.2.7 Paraboloids

For \(B=\operatorname{Diag}(1,1,0)\) and \(A=[0,0,-1]\) and \(d=0\) we get the paraboloid \(x^{2}+y^{2}=z\), for \(B=\operatorname{Diag}(1,-1,0)\) and \(A=[0,0,-1]\) and \(d=0\) we get the hyperbolic paraboloid \(x^{2}-y^{2}=z\). We can recognize paraboloids by intersecting with \(x=0\) or \(y=0\) to see parabola. Intersecting the elliptical paraboloid \(x^{2}+y^{2}=z\) with \(z=1\) gives an ellipse. Intersecting the hyperbolic paraboloid \(x^{2}-y^{2}=z\) with \(z=1\) gives a hyperbola.

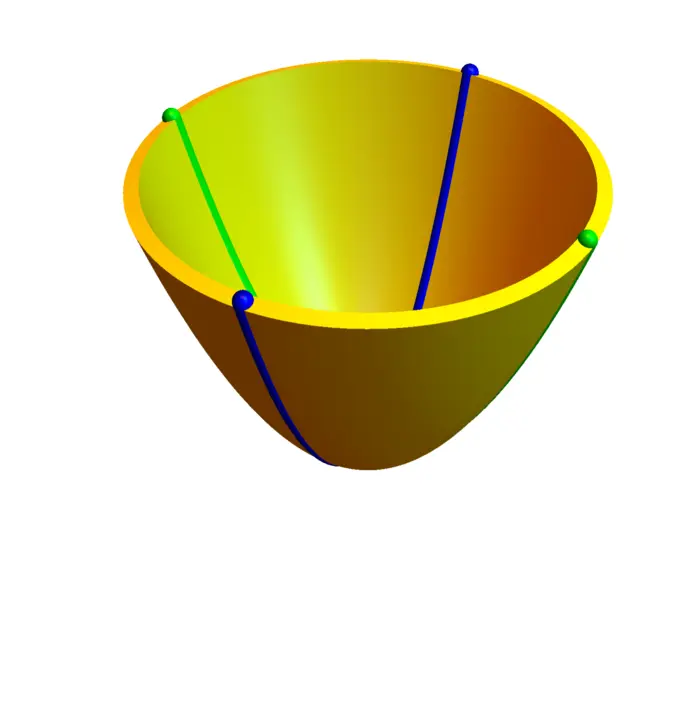
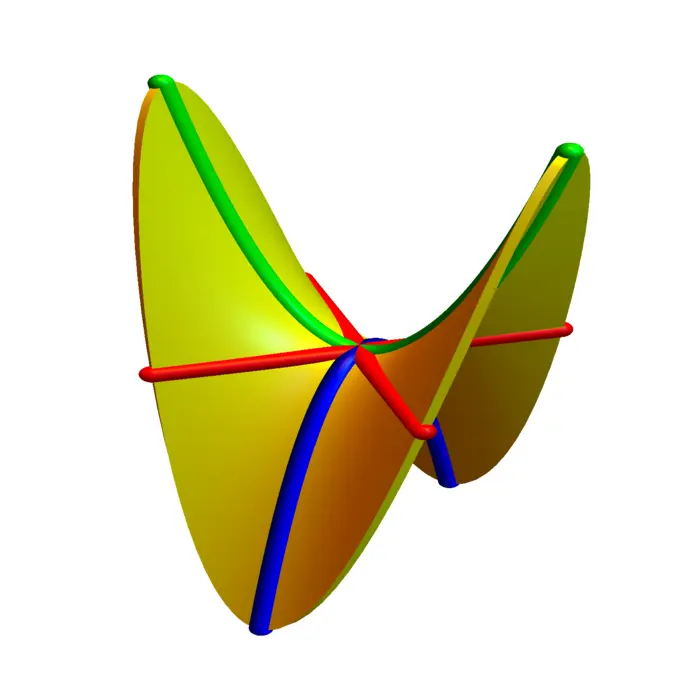
5.2.8 Special surfaces

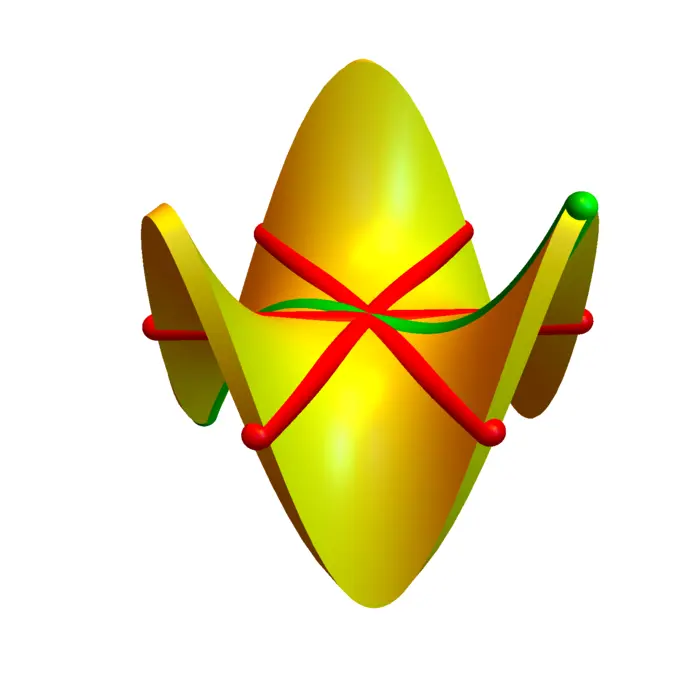
If \(B=\operatorname{Diag}(1,1,-1)\) and \(d=0\), we get a cone \(x^{2}+y^{2}-z^{2}= 0\). For \(B=\operatorname{Diag}(1,1,0)\) and \(d=1\) we get the cylinder \(x^{2}+y^{2}=1\).

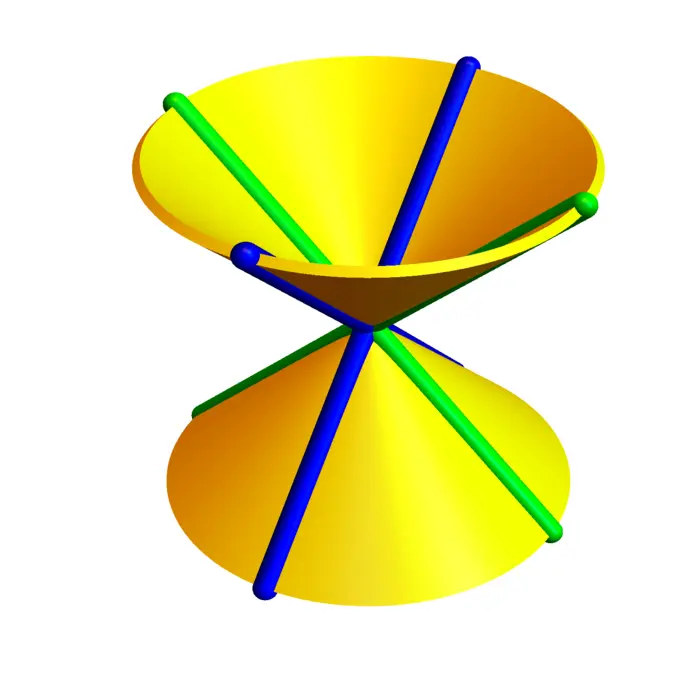
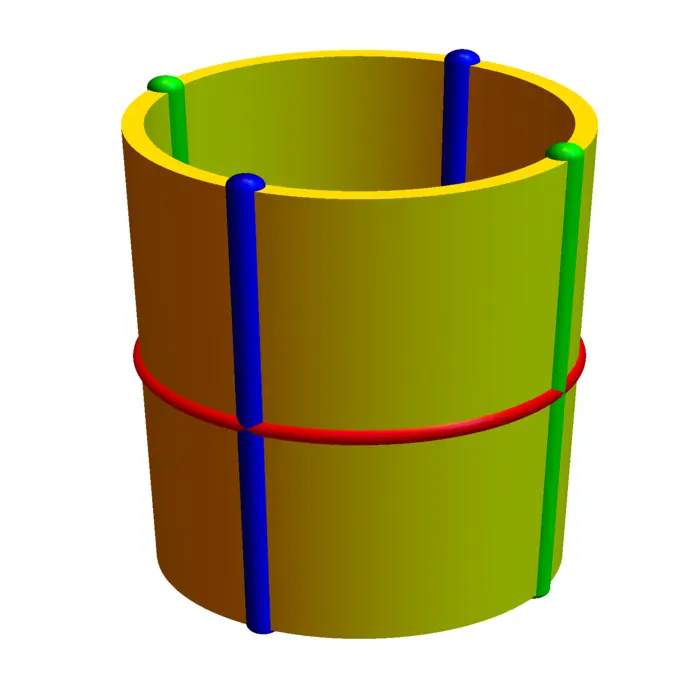
5.2.9 Side Remark: Algebraic Structures and Forces

The \(1\)-sphere \(S^{1}=\left\{x^{2}+y^{2}=1\right\} \subset \mathbb{R}^{2}\) and the \(3\)-sphere \(S^{3}=\left\{x^{2}+y^{2}+z^{2}+w^{2}=1\right\} \subset \mathbb{R}^{4}\) carry a multiplication: \(S^{1}\) is in the complex numbers \(\mathbb{C}=\{x+i y\}\) and \(S^{3}\) is in the quaternions \(\mathbb{H}=\{x+i y+j z+k w\}\). The \(1\)-sphere is the gauge group for electromagnetism, the \(3\)-sphere (also called \(S U(2)\)) is responsible for the weak force. No other Euclidean sphere carries a multiplication for which \(x \rightarrow x * y\) is smooth. Michael Atiyah once pointed out that this algebraic particularity might not be a coincidence and responsible for the structure of the standard model of elementary particles (one of the most accurate theories ever built by humanity). The strong force appears as one can let a set of \(3 \times 3\) matrices \(S U(3)\) act on \(\mathbb{H}\). Atiyah suggested that gravity could be related to the octonions \(\mathbb{O}\). There \(S^{7}=\{|x|=1\} \subset\) \(\mathbb{R}^{8}\) carries still a multiplication, but it is no more associative. The list of normed division algebras \(\mathbb{R}\), \(\mathbb{C}\), \(\mathbb{H}\) and \(\mathbb{O}\).¹

5.2.10 Polynomial Surfaces: Varieties

Given a polynomial \(p\) of \(n\) variables, one can look at the surface \(\{p(x)=0\}\). It is called a variety.

5.3 EXAMPLES

EXERCISES