Surface Area
Table of Contents
- 26.1 INTRODUCTION
- 26.2 LECTURE
- 26.2.1 Integration of Scalar Fields over Parametrized Surfaces
- 26.2.2 Transforming Integrals from One Surface to Another
- 26.2.3 Special Cases in Lower Dimensions
- 26.2.4 Parametrization Applications in Surface Integral Calculations
- 26.2.5 Volumes and Surface Areas of n-Dimensional Spheres using Hyperspherical Coordinates
- 26.3 EXAMPLES
- EXERCISES
26.1 INTRODUCTION
26.1.1 Flux Integrals over Parametrized Surfaces
We have looked at maps \(r: R \rightarrow S\) in the context of coordinate changes and also in full generality, in the case when \(R\) is a subset of \(\mathbb{R}^{m}\) and \(S\) is a subset of \(\mathbb{R}^{n}\). We have learned that the Jacobian matrix \(d r\) allows to quantify the distortion \(\sqrt{\operatorname{det}(d r^{T} d r)}\). If \(R\) is a subset of \(\mathbb{R}^{2}\), then \(r\) describes a \(2\)-dimensional surface. We usually write a point in \(R\) as \((u, v)\) but other variables can be used. If \(n=3\), that is if we deal with a surface in three dimensional space, then the distortion factor is \(|r_{u} \times r_{v}|\) and the surface area is the double integral \(\iint_{R}|r_{u} \times r_{v}| \,d u \,d v\). This topic is therefore a great opportunity to practice more double integrals.

26.2 LECTURE
26.2.1 Integration of Scalar Fields over Parametrized Surfaces
A map \(r: R \subset \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\) has an image \(r(R)=S\) which is a parametrized surface. What is its surface area? We have seen that the distortion factor is now \[|d r|=\sqrt{\det(g)}=|r_{u} \times r_{v}|,\] where \(g=d r^{T} d r\) was the first fundamental form of the surface. Of course, it is more convenient to use \(|r_{u} \times r_{v}|\), which is the same as \(|d r|\).
Theorem 1. The surface area \(\iint_{S} \,d S\) of \(S\) is \(\iint_{R}|r_{u} \times r_{v}| \,d u \,d v\).
26.2.2 Transforming Integrals from One Surface to Another
More generally if \(f: R \rightarrow \mathbb{R}\) is a function which describes something like a density then \(\iint_{R} f(r(u, v))|r_{u} \times r_{v}| \,d u \,d v\) is an integral which is abbreviated as \(\iint_{S} f \,d S\) and called a scalar surface integral. For example, if \(f\) is a density on the surface then this \(\iint_{S} f \,d S\) is the mass. Again, we have to stress that in this integral, the orientation of the surface is irrelevant. The distortion factor \(|d r|\) is always non-negative. It is better to think of \(\iint_{S} f \,d S\) as a A circle moving in space time produces a two dimensional surface. The surface area of this surface is of interest in physics. The surface area is the Nambu-Goto action. generalizing area \(\iint_{S} \,d S\).1
26.2.3 Special Cases in Lower Dimensions
Here is the most general change of integration formula for maps \(r: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\), with distortion factor \(|d r|=\sqrt{\operatorname{det}(d r^{T} d r)}\). The formula holds for \(m>n\) too, \(\det\) is then a pseudo determinant. If \(S=r(R)\) is the image of a solid \(R\) under a \(C^{2}\) map \(r\) and \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) is a function, then the mother of all substitution formulas is
Theorem 2. \(\iint_{R} f(r(u))|d r(u)| \,d u=\iint_{S} f(u) \,d u.\)
Proof. The proof is the same as seen in the two-dimensional change of variable situation. Just because \(n\) is used for the target space \(\mathbb{R}^{n}\), we use the basic size \(1 / N\). We chop up the region into parts \(R \cap Q\) with cubes \(Q\) of size \(1 / N\) and estimate the difference \(\operatorname{Vol}(d r(Q))\) and \(\operatorname{Vol}(r(Q))\) by \(C M_{N} / N^{2}\) leading to an overall difference bounded by \(F C M_{N} / N^{2}\), where \(F\) is the maximal value of \(f\) on \(R\) and \(M_{n}\) is the Heine-Cantor function modulus of continuity of \(f\). Adding everything up gives an error \[F C \operatorname{Vol}(R) M_{N}+2^{n} \operatorname{Vol}(\delta R) F / N \rightarrow 0,\] where \(\delta R\) is the boundary of \(R\). There is one new thing: we have to see why \(\sqrt{\operatorname{det}\left(A^{T} A\right)}\) is the volume of the parallelepiped spanned by the column vectors of the Jacobian matrix \(A=d r\). We will talk about determinants in detail later but if \(A\) is in row reduced echelon form then \(A^{T} A\) is the identity matrix and the determinant is \(1\), agreeing with the volume. Now notice that if a column of \(A\) is scaled by \(\lambda\) producing a new matrix \(B\), then \(\operatorname{det}(B^{T} A)=\lambda \operatorname{det}(A^{T} A)\) and \(\operatorname{det}(B^{T} B)=\lambda^{2} \operatorname{det}(A^{T} A)\). If two columns of \(A\) are swapped leading to a new matrix \(B\), then \(\operatorname{det}(B^{T} A)=-\operatorname{det}(A^{T} A)\) and \(\operatorname{det}(B^{T} B)=\operatorname{det}(A^{T} A)\). If a column of \(A\) is added to another column, then this does change \(\operatorname{det}(B^{T} B)\). The only row reduction step which affects the \(|d r|\) is the scaling. But that is completely in sync what happens with the volume. ◻
26.2.4 Parametrization Applications in Surface Integral Calculations
The last theorem covers everything we have seen and we ever need to know when integrating scalar functions over manifolds. In the special case \(n=m\) it leads to:
Theorem 3. \(\iint_{R}|d r(u)| \,d u=\operatorname{Vol}(S)\).
26.2.5 Volumes and Surface Areas of n-Dimensional Spheres using Hyperspherical Coordinates
Here are the important small dimensional examples:
- If \(m=1\), \(n=3\), then \(\int_{a}^{b}|r^{\prime}(t)| \,d t\) is the arc length of the curve \(C=r(I)\).
- If \(m=2\), \(n=2\), then \(\iint_{R}|d r| \,d u \,d v\) is the area of the region \(S=r(R)\).
- If \(m=2\), \(n=3\), then \(\iint_{R}|r_{u} \times r_{v}| \,d u \,d v\) is the surface area of \(S=r(R)\).
- If \(m=3\), \(n=3\), then \(\iiint_{R}|d r| \,d u \,d v \,d w\) is the volume of the solid \(S=r(R)\).
26.3 EXAMPLES
Example 1. In all the examples of surface area computations, we take a parametrization \(r(u, v): R \rightarrow S\), then use use that the distortion factor is \(\sqrt{\operatorname{det}(d r^{T} d r)}=|r_{u} \times r_{v}|\).
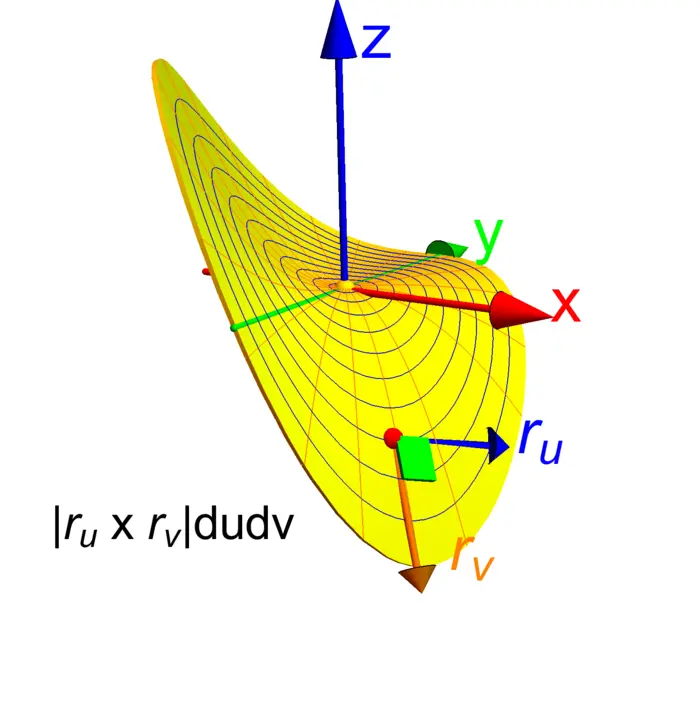
Example 2. Problem: find the surface area of a sphere \(x^{2}+y^{2}+z^{2}=L^{2}\).
Solution: Parametrize the surface \[r([\theta, \phi])=[L \sin (\phi) \cos (\theta), L \sin (\phi) \sin (\theta), L \cos (\phi)].\] The distortion factor is \(L^{2} \sin (\phi)\). The surface area is \(4 \pi L^{2}\).
Example 3. Problem: find the surface area of surface of revolution given in cylindrical coordinates as \(z=g(\theta)\), \(a \leq z \leq b\).
Solution: Parametrize the surface \[r([\theta, z])=[g(z) \cos (\theta), g(z) \sin (\theta), z].\] The distortion factor is \(g(z) \sqrt{1+g^{\prime}(z)^{2}}\). As an example, we can look at the surface of revolution \(x^{2}+y^{2}=1 / z^{2}\), \(|z|^{2}>1\). The volume of the solid enclosed by the surface is \(\pi\). The surface area is infinite.
Example 4. Problem: find the surface area of the graph of a function \(z=f(x, y)\), \((x, y) \in R\).
Solution: Parametrize the surface as \(r([x, y])=[x, y, f(x, y)]\). The distortion factor is \[|r_{x} \times r_{y}|=\sqrt{1+f_{x}^{2}+f_{y}^{2}}.\]
Example 5. Problem: what is the surface area of the intersection of \(x^{2}+z^{2} \leq 1\), \(6 x+3 y+9 z=12\)?
Solution: The surface is a plane but also a graph over \(R=\{x^{2}+z^{2} \leq 1\}\) in the \(xz\)-plane. The simplest parametrization is \[r([x, z])=[x,(12-6 x-9 z) / 3, z]=[x, 4-2 x-3 z, z].\] It gives \(|r_{x} \times r_{z}|=|[-2,-1,-3]|=\sqrt{14}\). The surface area is \[\iint_{R} \sqrt{14} \,d x \,d y=\sqrt{14} \operatorname{Area}(R)=\sqrt{14} \pi.\]
Example 6. The following hyperspherical coordinates parametrize the \(3\)-dimensional sphere \(x^{2}+y^{2}+z^{2}+w^{2}=1\) in \(\mathbb{R}^{4}\). \[r([\phi, \psi, \theta])=[\cos (\phi), \sin (\phi) \cos (\psi), \sin (\phi) \sin (\psi) \cos (\theta), \sin (\phi) \sin (\psi) \sin (\theta)]\] with \(\theta \in[0,2 \pi]\), \(\phi \in[0, \pi]\), \(\psi \in[0, \pi]\). The distortion factor is \[\sqrt{\operatorname{det}(d r^{T} d r)}=\sqrt{\sin ^{4}(\phi) \sin ^{2}(\psi)}\] so that the surface area of the hypersphere is \[2 \pi \int_{0}^{\pi} \int_{0}^{\pi} \sin ^{2}(\phi) \sin (\psi) \,d \phi \,d \psi=\fbox{$2 \pi^{2}$}.\]
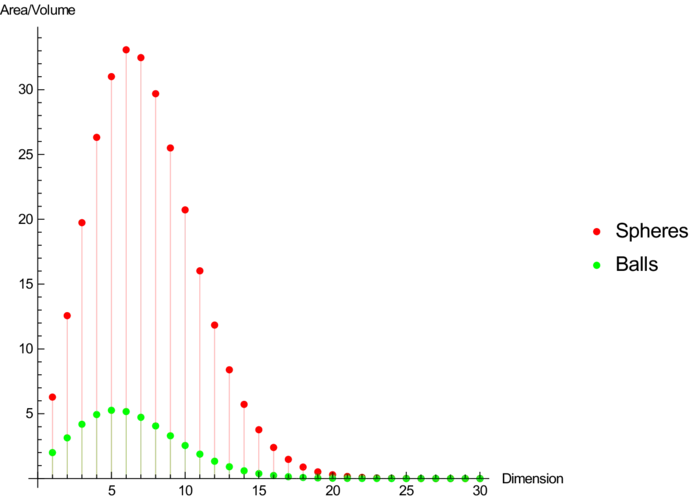
Example 7. In dimension \(n\) what is the volume \(|B_{n}|\) of the \(n\)-dimensional unit ball \(B_{n}\) in \(\mathbb{R}^{n}\) and the volume \(|S_{n}|\) of the \(n\)-dimensional unit sphere \(S_{n}\) in \(\mathbb{R}^{n+1}\)? It starts with \(|B_{0}|=1\), as \(B_{0}\) is a point and \(|S_{0}|=2\), as \(S_{0}\) consists of two points. The \(n\)-ball of radius \(\rho\) has the volume \(|B_{n}| \rho^{n}\) and the \(n\)-sphere of radius \(\rho\) has the volume \(|S_{n}| \rho^{n}\). Because \(|B_{n+1}|=\int_{0}^{1}|S_{n}| \rho^{n} \,d \rho\), we have \(|B_{n+1}|=|S_{n}| /(n+1)\). Because \(S_{n}\) can be written as a union of products \((n-2)\)-spheres with \(S_{1}\) leading to \[|S_{n}|=2 \pi \int_{0}^{\pi / 2}|S_{n-2}| \cos (\phi) \,d \phi=2\pi|B_{n-1}|.\] We know now all: just start with \(|B_{0}|=1\), \(|S_{0}|=2\), \(|B_{1}|=2\), \(|S_{1}|=2 \pi\) and
Theorem 4. \(|B_{n}|=\frac{2 \pi}{n}|B_{n-2}|\), \(|S_{n}|=\frac{2 \pi}{n-1}|S_{n-2}|\).
The \(5\)-ball has maximal volume \(5.26379\ldots\) among all unit balls. The \(6\)-sphere has maximal surface area \(33.0734 \ldots\) among all unit spheres. The volume of the \(30\)-ball is only \(0.00002\ldots\) The surface area of the \(30\)-sphere for example is only \(0.0003\). Compare with an \(\boldsymbol{n}\)-unit cube of volume \(1\) and a boundary surface area \(2n\). High dimensional spheres and balls are tiny!
Example 8. If \(S\) is a cylinder \(x^{2}+y^{2}=1\), \(0
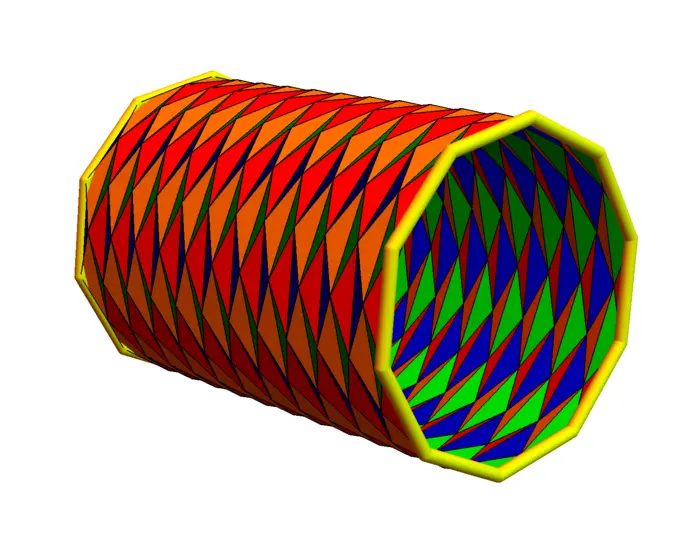
Example 9. The three dimensional sphere is \(x^{2}+y^{2}+z^{2}+w^{2}=1\) in \(\mathbb{R}^{4}\). The Hopf parametrization is \(r: R \subset \mathbb{R}^{3} \rightarrow S \subset \mathbb{R}^{4}\) is \[r\big([\phi, \theta_{1}, \theta_{2}]\big)=\big[\cos (\phi) \cos (\theta_{1}), \cos (\phi) \sin (\theta_{1}), \sin (\phi) \cos (\theta_{2}), \sin (\phi) \sin(\theta_{2})\big].\] We compute \[|d r|=\sqrt{\operatorname{det}(d r^{T} d r)}=\cos (\phi) \sin (\phi)=\sin (2 \phi) / 2.\] If we fix \(\phi\), we see a two dimensional torus. Their union with \(\phi \in[0, \pi / 2]\) is the Hopf fibration. We can now compute the volume of the three dimensional sphere: \[\int_{0}^{\pi / 2} \int_{0}^{2 \pi} \int_{0}^{2 \pi} \sin (2 \phi) / 2 \,d \phi \,d \theta_{1} \,d \theta_{2}=2 \pi^{2}.\]

EXERCISES
Exercise 1. Find the moment of inertia \[\iiint_{E} (x^{2}+y^{2}) \,d V,\] where \(E=\{x^{2}+y^{2} \leq z^{2},\ |z|^{2} \leq 1\}\) is the double cone.
Exercise 2. Evaluate the triple integral \[\iiint_{E} x y \,d V\] where \(E\) is bounded by the parabolic cylinders \(y=3 x^{2}\) and \(x=3 y^{2}\) and the planes \(z=0\) and \(z=x+y\).
Exercise 3. We have seen the problem in the movie "Gifted" to compute the improper integral of \(e^{-x^{2}}\). Here is another approach: verify \[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^{2}+y^{2}+z^{2})} \,d x \,d y \,d z=(\sqrt{\pi})^{3}\] Use this as in the "Gifted" computation to find \(\int_{-\infty}^{\infty} e^{-x^{2}} \,d x\). You can do that without knowing that the later is \(\sqrt{\pi}\).
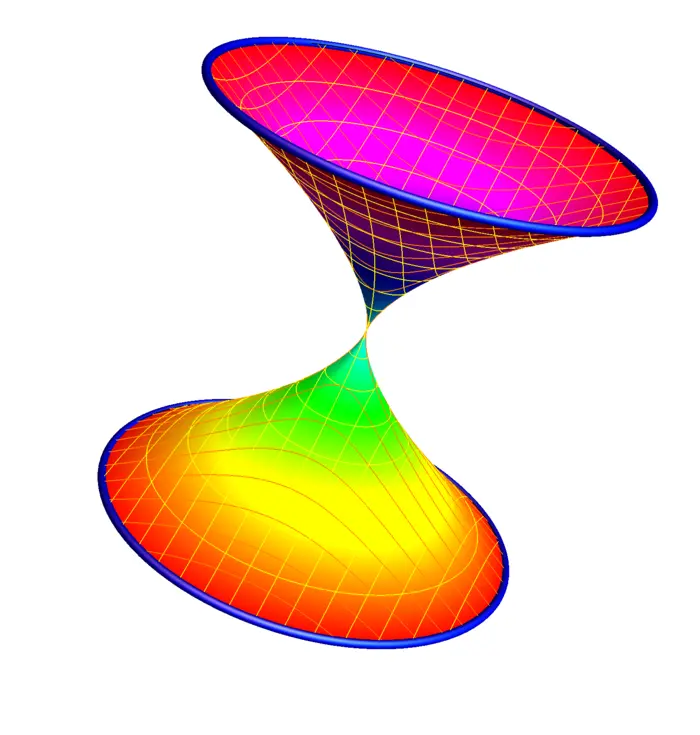
Exercise 4. Find the surface area of the Einstein-Rosen bridge \[r(u, v)=[3 v^{3}, v^{9} \cos (u), v^{9} \sin (u)]^{T},\] where \(0 \leq u \leq 2 \pi\) and \(-1 \leq v \leq\) 1. Tunnels connecting different parts of space-time appear frequently in science fiction.
Exercise 5. Find the area of the surface given by the helicoid \[r(u, v)=[u \cos (v), u \sin (v), v]^{T}\] with \(0 \leq u \leq 1\), \(0 \leq v \leq \pi\).
- Unfortunately, scalar integrals are often placed close to the integration of differential forms (like volume forms). The later are of different nature and use an integration theory in which spaces come with orientation. So far, if we replace \(r(u, v)\) with \(r(v, u)\) gives the same result (like area or mass).↩︎