Solids
Table of Contents
25.1 INTRODUCTION
25.1.1 Beyond Surfaces: 3D Solids
\(1\)-dimensional objects are curves and \(2\)-dimensional objects are regions or surfaces. In dimension \(3\), we deal with solids. The simplest solids imaginable are the cube or the spherical ball. Solids in three dimensional space are usually drawn by plotting their boundary surfaces. A solid polyhedron for example is bound by planes. The first figure shows the solid bound by hyperboloids. It is quite a challenge to compute its volume.1

25.1.2 Building Dimensions: Length, Area, and Now Volume
While curves \(C\) have length and regions \(S\) have area, three dimensional solids \(E\) have volume. We will in the next lecture look at surface area \(\iint_{S} 1 \,d S\). In this lecture we look at volume \(\iiint_{E} 1 \,d V\).
25.2 LECTURE
25.2.1 From Basic Solids to Triple Integrals
A basic solid \(R\) in \(\mathbb{R}^{n}\) is a bounded region enclosed by finitely many surfaces \(g_{i}(x_{1}, \ldots, x_{n})=c_{i}\). A solid is a finite union of such basic solids. We focus here mostly on \(n=3\). A \(3\)D integral \(I=\iiint_{R} f(x, y, z) \,d x \,d y \,d z\) is defined in the same way as a limit of a Riemann sum \(I_{n}\) which for a given integer \(n\) is defined as \[I_{n}=\frac{1}{n^{3}} \sum_{(\frac{i}{n}, \frac{j}{n}, \frac{k}{n}) \in R} f\Big(\frac{i}{n}, \frac{j}{n}, \frac{k}{n}\Big).\] The convergence is proven in the same way. The boundary contribution can be neglected in the limit \(n \rightarrow \infty\). If \(\Phi: R \rightarrow E\) is a parametrization of the solid, then
Theorem 1. \[\iiint_{R} f(u, v, w)|d \Phi(u, v, w)| \,d u \,d v \,d w=\iiint_{E} f(x, y, z) \,d x \,d y \,d z.\]




25.2.2 Computing Volumes with 3D Integrals and Change of Variables
If \(f(x, y, z)\) is constant \(1\), then \(\iiint_{E} f(x, y, z) \,d x \,d y \,d z\) is the volume of the solid \(E\). For a cone \[x^{2}+y^{2} \leq z^{2}, \quad 0 \leq z \leq 1,\] we can write \[\iiint 1 \,d z \,d x \,d y=\iint_{R} \big(1-\sqrt{x^{2}+y^{2}}\big) \,d x \,d y,\] where \(R\) is the unit disc. Its volume is \(\pi-2 \pi / 3=\pi / 3\). For the unit sphere \(x^{2}+y^{2}+z^{2} \leq 1\) for example, we can write \[\iiint_{E} 1 \,d z \,d x \,d y=\iint_{R} 2 \sqrt{1-x^{2}-y^{2}} \,d x \,d y,\] where \(R\) is the unit disc \(x^{2}+y^{2} \leq 1\). In polar coordinates, we get \[\int_{0}^{2 \pi} \int_{0}^{1} 2 \sqrt{1-r^{2}} r \,d r \,d \theta=4 \pi / 3.\] We can also use spherical coordinates \[\Phi([\rho, \phi, \theta])=[\rho \sin (\phi) \cos (\theta), \rho \sin (\phi) \sin (\theta), \rho \cos (\phi)],\] where \(|d \Phi|=\rho^{2} \sin (\phi)\). The volume is \[\int_{0}^{2 \pi} \int_{0}^{\pi} \int_{0}^{1} \rho^{2} \sin (\phi) \,d \rho \,d \phi \,d \theta=4 \pi / 3.\]
25.2.3 Two Key Approaches to 3D Integration
There are two basic strategies to compute the integral: the first is to slice the region up along a line like the \(z\)-axis then form \(\int_{a}^{b} \iint_{R(z)} f(x, y, z) \,d x \,d y \,d z\). To get the volume of a cone for example, integrate \(\int_{0}^{1}\left[\iint_{R(z)} 1 \,d x \,d y\right] d z\). The inner double integral is the area of the slice which is \(\pi z^{2}\). The last integral gives \(\pi / 3\). A second reduction is to see the solid sandwiched between two graphs of a function on a region \(R\), then form \(\iint_{R}\left[\int_{g(x, y)}^{h(x, y)} f(x, y, z) \,d z\right] d x \,d y\). In the cone case, we have for \(R\) the disc of radius \(1\). The lower function is \(g(x, y)=\sqrt{x^{2}+y^{2}}\) the upper function is \(1\). We get \(\iint_{R}\left[1-\sqrt{x^{2}+y^{2}}\right] d x \,d y\), a double integral which best can be computed using polar coordinates: \[\int_{0}^{2 \pi} \int_{0}^{1}(1-r) r \,d r \,d \theta=2 \pi(1 / 2-1 / 3)=\pi / 3.\] Burgers and fries!
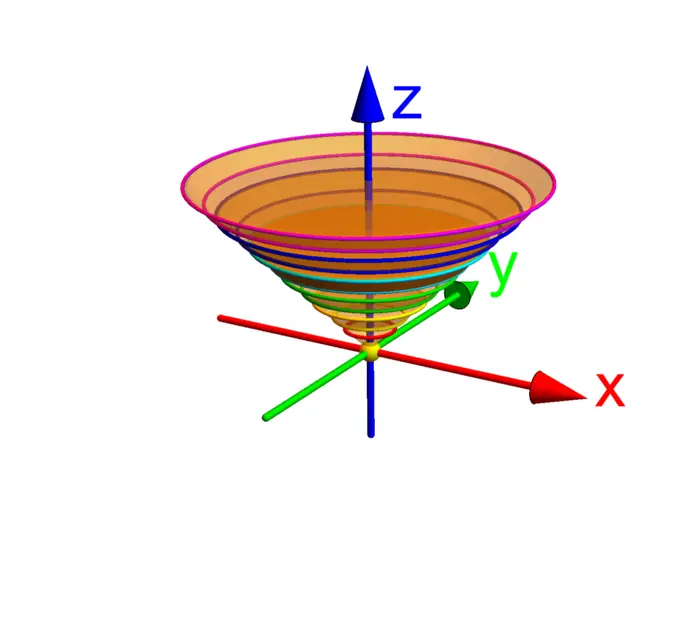
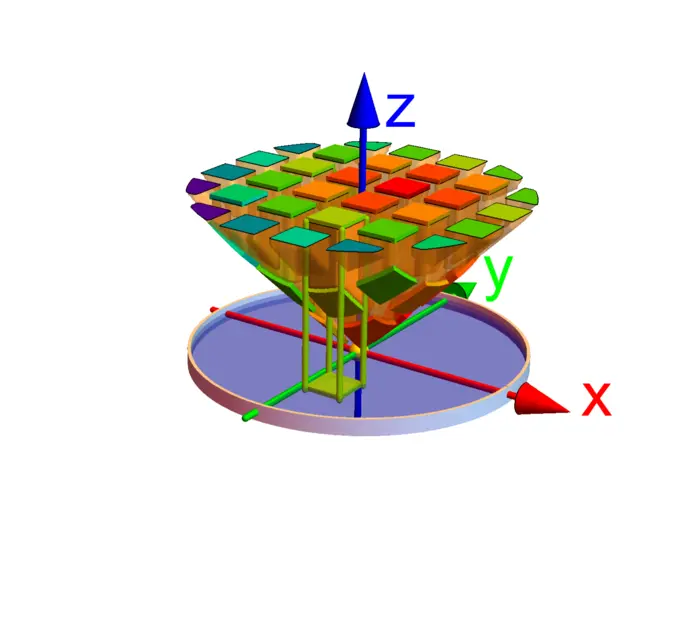
25.2.4 Jacobians for Spherical and Cylindrical Coordinates
We have seen in the theorem the coordinate change formula if \(\Phi: R \rightarrow E\) is given. For spherical coordinates \[\Phi([\rho, \phi, \theta])=[\rho \sin (\phi) \cos (\theta), \rho \sin (\phi) \sin (\theta), \rho \cos (\phi)],\] we have . For cylindrical coordinates, the situation is the same as for polar coordinates. The map \[\Phi([r, \theta, z])=[r \cos (\theta), r \sin (\theta), z]\] produces .
25.2.5 Ellipsoid Volume
Let us find the integral \(\iiint_{E} 1 \,d x \,d y d z\), where \[E=\left\{x^{2} / a^{2}+y^{2} / b^{2}+z^{2} / c^{2} \leq 1\right\}\] is a solid ellipsoid. The most comfortable way is to introduce another coordinate change \(\Psi([x, y, z]) \rightarrow[a x, b y, c z]\) which maps the solid sphere \(S\) to to the solid ellipsoid \(E\). Then take the spherical coordinate map \(\phi: R \rightarrow S\), where \[R=\{(\rho, \phi, \theta) \mid 0 \leq \rho \leq 1,\ 0 \leq \phi \leq \pi,\ 0 \leq \theta \leq 2 \pi\}.\] Now \(\Psi \circ \Phi: R \rightarrow E\) is a coordinate change which maps \(R\) to the ellipsoid. By the chain rule, the distortion factor is \(|d \Psi||d \Phi|=a b c \rho^{2} \sin (\phi)\). The integral is \[a b c(1 / 3)(2 \pi) \int_{0}^{\pi} \sin (\phi) \,d\phi= \fbox{$(4 \pi / 3)(a b c)$}.\]
25.2.6 Solid Torus Volume: A Special Coordinate System
In order to compute the volume of a solid torus, we can introduce a special coordinate system \[\Phi([r, \psi, \theta])=[(b+ar\cos (\psi)) \cos (\theta),(b+ar\cos (\psi)) \sin (\theta), a \sin (\psi)].\] The solid torus \(E\) is then the image of the cuboid \[\{(r, \psi, \theta) \mid 0 \leq r \leq 1,\ 0 \leq \psi \leq 2 \pi,\ 0 \leq \theta \leq 2 \pi\}.\] The determinant is \(|d \Phi|=a^{2} \cos ^{2}(s)(b+ar\cos (s))\). Integration over the cuboid gives the volume \((2 \pi b)(\pi a^{2})\).
25.3 EXAMPLES
Example 1. To find \(\iiint_{E} f \,d V\) for \[E=\{0 \leq x \leq 1,\ 0 \leq y \leq 1,\ 0 \leq z \leq 1\} \quad \text{and} \quad f(x, y, z)=24 x^{2} y^{3} z,\] set up the integral \(\int_{0}^{1} \int_{0}^{1} \int_{0}^{1} 24 x^{2} y^{3} z \,d z \,d y \,d x\). Start with the core \(\int_{0}^{1} 24 x^{2} y^{3} z \,d z=12 x^{3} y^{3}\), then integrate the middle layer, \(\int_{0}^{1} 12 x^{3} y^{3} \,d y=3 x^{2}\) and finally handle the outer layer: \(\int_{0}^{1} 3 x^{2} \,d x=1\).
Example 2. To find the moment of inertia \(I=\iiint_{E} (x^{2}+y^{2}) \,d V\) of a sphere \(E=\left\{x^{2}+y^{2}+z^{2} \leq L^{2}\right\}\), we use spherical coordinates. We know that \(x^{2}+y^{2}=\rho^{2} \sin ^{2}(\phi)\) and the distortion factor is \(\rho^{2} \sin (\phi)\). We have therefore \[I=\int_{0}^{2 \pi} \int_{0}^{\pi} \int_{0}^{L} \rho^{2} \sin ^{2}(\phi) \rho^{2} \sin (\phi) \,d \rho \,d \phi \,d \theta=8 \pi L^{5} / 15.\] We will see some details in class. If we rotate the sphere around the \(z\)-axis with angular velocity \(\omega\), then \(I \omega^{2} / 2\) is the kinetic energy of that sphere. For example, the moment of inertia of the earth is \(8 \cdot 10^{37}\ \mathrm{kgm}^{2}\). With an angular velocity of \(\omega=2 \pi / \mathrm{day} = 2 \pi /(86400 \ \mathrm{s})\), this rotational kinetic energy is \[8 \cdot 10^{37}\ \mathrm{kgm}^{2} /(7464960000\ \mathrm{s}^{2}) \sim 10^{29}\ \mathrm{J} \sim 2.5 \cdot 10^{24}\ \mathrm{kcal}.\]
Example 3. Problem: Find the volume \(E\) of the intersection of \(x^{2}+y^{2} \leq 1\), \(x^{2}+z^{2} \leq 1\) and \(y^{2}+z^{2} \leq 1\).
Solution: look at \(1 / 16\)’th of the body given in cylindrical coordinates \(0 \leq \theta \leq \pi / 4\), \(r \leq 1, z>0\). The roof is \(z=\sqrt{1-x^{2}}\) because above the "one eighth disc" \(R\) only the cylinder \(x^{2}+z^{2}=1\) matters. The polar integration problem \[16 \int_{0}^{\pi / 4} \int_{0}^{1} \sqrt{1-r^{2} \cos ^{2}(\theta)} r \,d r \,d \theta\] has an inner \(r\)-integral of \((16 / 3)\big(1-\sin^3 (\theta)\big) / \cos ^{2}(\theta)\). Integrating this over \(\theta\) can be done by integrating \(f(x)=\big(1-\sin^3(x)\big) \sec ^{2}(x)\) by parts (using \(\tan^{\prime}(x)=\sec ^{2}(x)\)) leading to the anti-derivative \(-\cos (x)+\sec (x)+\tan (x)\) of \(f\). The result is \(16-8 \sqrt{2}\).
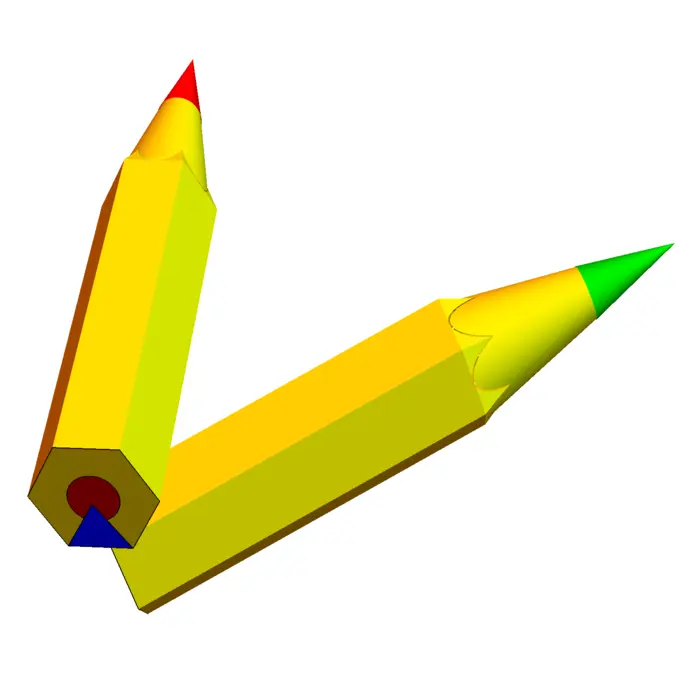
Example 4. Problem: A pencil \(E\), a hexagonal cylinder of radius \(1\) above the \(x y\)-plane is cut by a sharpener below the cone \(z=10-r\). What is its volume?
Solution: we consider one sixth of the pen where the base is the polar region \(0 \leq \theta \leq 2 \pi / 6\) and \(r(\theta) \leq \sqrt{3} /(\sqrt{3} \cos (\theta)+\sin (\theta))\). The pen’s back is \(z=0\) and the sharpened part is \(z=10-r\). \[\int_{0}^{\pi / 3} \int_{0}^{\sqrt{3} /(\sqrt{3} \cos (t)+\sin (t))} \int_{0}^{10-r} 1 r \,d z \,d r \,d \theta.\] The integral can be computed and is a bit messy \(\big(29-3 \operatorname{arctanh}(2-\sqrt{3})\big) /(3 \sqrt{3})\).2