Second Hourly

28.1 Keywords for Second Hourly
28.2 Second Hourly (Practice A)
28.3 Second Hourly (Practice B)
28.4 Second Hourly

28.1 Keywords for Second Hourly

This is a bit of a checklist. Make your own list. But here is a checklist which tries to be comprehensive. Check off the topics you know and check back with things you do not recall. You will need to have the following on your finger tips.

28.1.1 Partial Derivatives

$f_{x}(x, y)=\frac{\partial}{\partial x} f(x, y)$ partial derivative
$L(x, y)=f(x_{0}, y_{0})+f_{x}(x_{0}, y_{0})(x-x_{0})+f_{y}(x_{0}, y_{0})(y-y_{0})$ linear approximation
$Q(x, y)=L(x_{0}, y_{0})+f_{x x}(x-x_{0})^{2} / 2+f_{y y}(y-y_{0})^{2} / 2+f_{x y}(x-x_{0})(y-y_{0})$ quadratic
$L(x, y)$ estimates $f(x, y)$ near $f(x_{0}, y_{0})$. The result is $f(x_{0}, y_{0})+a(x-x_{0})+b(y-y_{0})$
tangent line: $a x+b y=d$ with $a=f_{x}(x_{0}, y_{0})$, $b=f_{y}(x_{0}, y_{0})$, $d=a x_{0}+b y_{0}$
tangent plane: $a x+b y+c z=d$ with $a=f_{x}$, $b=f_{y}$, $c=f_{z}$, $d=a x_{0}+b y_{0}+c z_{0}$
estimate $f(x, y, z)$ by $L(x, y, z)$ near $(x_{0}, y_{0}, z_{0})$
$f_{x y}=f_{y x}$ Clairaut’s theorem, if $f_{x y}$ and $f_{y x}$ are continuous.
$r_{u}(u, v)$, $r_{v}(u, v)$ tangent to surface parameterized by $r(u, v)$

28.1.2 Partial Differential Equations

$f_{t}=f_{x x}$ heat equation
$f_{t t}-f_{x x}=0$ wave equation
$f_{x}-f_{t}=0$ transport equation
$f_{x x}+f_{y y}=0$ Laplace equation
$f_{t}+f f_{x}=f_{x x}$ Burgers equation
$f_{x}^{2}+f_{y}^{2}=1$ Eiconal equation
$f_{t}=f-x f_{x}-x^{2} f_{x x}$ Black Scholes

28.1.3 Gradient

$\nabla f(x, y)=d f^{T}=[f_{x}, f_{y}]^{T}$, $\nabla f(x, y, z)=[f_{x}, f_{y}, f_{z}]^{T}$, gradient
$D_{v} f=\nabla f \cdot v$ directional derivative
$\frac{d}{d t} f(r(t))=\nabla f(r(t)) \cdot r^{\prime}(t)$ chain rule
$\nabla f(x_{0}, y_{0})$ is orthogonal to the level curve $f(x, y)=c$ containing $(x_{0}, y_{0})$
$\nabla f(x_{0}, y_{0}, z_{0})$ is orthogonal to the level surface $f(x, y, z)=c$ containing $(x_{0}, y_{0}, z_{0})$
$\frac{d}{d t} f(x+t v)=D_{v} f$ by chain rule
$(x-x_{0}) f_{x}(x_{0}, y_{0}, z_{0})+(y-y_{0}) f_{y}(x_{0}, y_{0}, z_{0})+(z-z_{0}) f_{z}(x_{0}, y_{0}, z_{0})=0$ tangent plane
$f(x, y)$ increases in the $\nabla f /|\nabla f|$ direction. Functions dance upwards.
$f(x, y, z)=c$ defines $z=g(x, y)$, and $g_{x}(x, y)=-f_{x}(x, y, z) / f_{z}(x, y, z)$ implicit diff

28.1.4 Extrema

$\nabla f(x, y)=[0,0]^{T}$, critical point or stationary point
$D=f_{x x} f_{y y}-f_{x y}^{2}=\operatorname{det}(d f)$ discriminant, useful in second derivative test
$f(x_{0}, y_{0}) \geq f(x, y)$ in a neighborhood of $(x_{0}, y_{0})$ local maximum
$f(x_{0}, y_{0}) \leq f(x, y)$ in a neighborhood of $(x_{0}, y_{0})$ local minimum
$\nabla f(x, y)=\lambda \nabla g(x, y)$, $g(x, y)=c$, or $\nabla g=0$ Lagrange equations
second derivative test: $\nabla f=(0,0)$, $D>0$, $f_{x x}<0$ local max, $\nabla f=(0,0)$, $D>0$, $f_{x x}>0$ local min, $\nabla f=(0,0)$, $D<0$ saddle point
$f(x_{0}, y_{0}) \geq f(x, y)$ everywhere, global maximum
$f(x_{0}, y_{0}) \leq f(x, y)$ everywhere, global minimum
$f$ is Morse if the Hessian $H=d^{2} f$ is invertible at every critical point

28.1.5 Double Integrals

$\iint_{R} f(x, y) \,d y \,d x$ double integral
$\int_{a}^{b} \int_{c(x)}^{d(x)} f(x, y) \,d y \,d x$ bottom-to-top region
$\int_{c}^{d} \int_{a(y)}^{b(y)} f(x, y) \,d x \,d y$ left-to-right region
$\iint_{R} f(r, \theta) \fbox{$r$} \,d r \,d \theta$ polar coordinates
$\iint_{R}|r_{u} \times r_{v}| \,d u \,d v$ surface area
$\int_{a}^{b} \int_{c}^{d} f(x, y) \,d y \,d x=\int_{c}^{d} \int_{a}^{b} f(x, y) \,d x \,d y$ Fubini
$\iint_{R} \fbox{$1$} \,dx \,dy$ area of region $R$
$\iint_{R} f(x, y) \,d x \,d y$ signed volume of solid bound by graph of $f$ and $x y$-plane

28.1.6 Triple Integrals

$\iiint_R f(x, y, z) \,dz \,dy \,dx$ triple integral
$\int_a^b \int_c^d \int_u^v f(x, y, z) \,dz \,dy \,dx$ integral over rectangular box
$\int_a^b \int_{g_1(x)}^{g_2(x)} \int_{h_1(x, y)}^{h_2(x, y)} f(x, y) \,dz \,dy \,dx$ type I region
$\iiint_R f(r, \theta, z) \fbox{$r$} \,dz \,dr \,d\theta$ integral in cylindrical coordinates
$\iiint_R f(\rho, \theta, \phi) \fbox{$\rho^2 \sin(\phi)$} \,d\rho \,d\phi \,d\theta$ integral in spherical coordinates
$\int_a^b \int_c^d \int_u^v f(x, y, z) \,dz \,dy \,dx = \int_u^v \int_c^d \int_a^b f(x, y, z) \,dx \,dy \,dz$ Fubini
$V = \iiint_E \fbox{$1$} \,dz \,dy \,dx$ volume of solid $E$
$M = \iiint_E f(x, y, z) \,dz \,dy \,dx$ mass of solid $E$ with density $f$

28.1.7 General advise

Draw the region when integrating in in higher dimensions.
Consider other coordinate systems if the integral does not work.
Consider changing the order of integration if the integral does not work.
For tangent planes, compute the gradient $[a, b, c]^{T}$ first then fix the constant.
When looking at relief problems, mind the gradient.

28.1.8 Theorems

Clairaut, Taylor, Fubini, Island theorem, Sphere and Ball volumes, Morse theorem, chain rule, gradient theorem, change of variables

28.1.9 People

Clairaut, Fubini, Lagrange, Fermat, Riemann, Archimedes, Hamilton, Euler, Taylor, Morse, Hopf, Tao, Polya, Riemann

28.2 Second Hourly (Practice A)

You only need this booklet and something to write. Please stow away any other material and electronic devices. Remember the honor code.
Please write neatly and give details. Except for problems 28.2 and 28.3, we want to see details, even if the answer should be obvious to you.
Try to answer the question on the same page. There is also space on the back of each page.
If you finish a problem somewhere else, please indicate on the problem page so that we find it.
You have 75 minutes for this hourly.

Archimedes sends his good luck wishes. He unfortunately can not join us as he is "busy proving a new theorem". He just sent us his selfie. Oh well, these celebrities!

Problem 28A.1 (10 points):

(4 points) Prove that if $x^{3}$ is irrational, then $x$ is irrational.
(3 points) Prove or disprove: the product of two odd integers is odd.
(3 points) Prove or disprove: the sum of two odd integers is odd.

Problem 28A.2 (10 points, each question is one point):

What is the name of the partial differential equation $f_{t t}=f_{x x}$?
The series \[f(x)=\sum_{k=0}^{\infty} x^{k} / k !=1+x+x^{2} / 2 !+x^{3} / 3 !+\cdots\] represents a function. Which one?
The implicit differentiation formula for $f(x, y(x))=1$ is $y^{\prime}(x)=\ldots \ldots$.
What is the name of the function $f(s)=\sum_{n=1}^{\infty} n^{-s}$?
On a circular island there are exactly $3$ maxima and one minimum for the height $f$. Assuming $f$ is a Morse function, how many saddle points are there?
Which mathematician first found the value for the volume of the ball $x^{2}+y^{2}+z^{2} \leq 1$?
True or False: the directional derivative of $f$ in the direction $\nabla f(x) /|\nabla f(x)|$ is negative at a point where $\nabla f$ is not zero.
The equation \[f(x+t)=e^{D t} f=f(x)+f^{\prime}(x) t+f^{\prime \prime}(x) t^{2} / 2+\cdots\] solves a partial differential equation. Which one?
What is the formula for the surface area of a surface $S$ parametrized by $r(u, v)$ over a domain $R$?
What is the integration factor (= distortion factor) when going to spherical coordinates $(\rho, \phi, \theta)$?

Problem 28A.3 (10 points, each question is two points):

We see the level curves of a Morse function $f$. The circle through $A B C$ will sometimes serve as a constraint $g(x, y)=x^{2}+y^{2}=1$. In all questions, we only pick points from $A$, $B$, $C$, $D$, $E$, $F$, $G$, $H$, $I$, $J$, $K$, $L$, $M$.

Which points are local minima of $f$ under the constraint $g(x, y)=1$?
Which points are local maxima of $f$ under the constraint $g(x, y)=1$?
At which points do we have $f_{x}(x, y) \cdot f_{y}(x, y) \neq 0$?
At which points are $|\nabla f(x, y)|$ maximal?
At which points are $|\nabla f(x, y)|$ minimal?

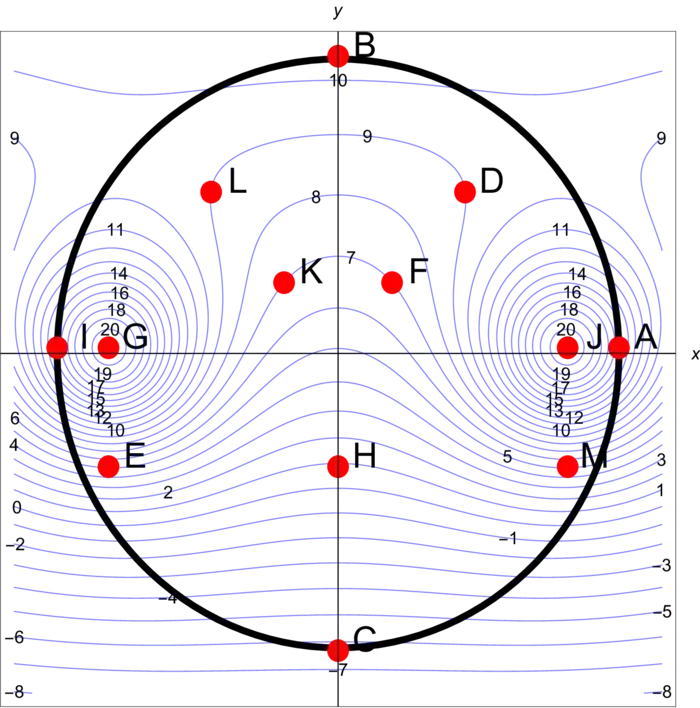
Problem 28A.4 (10 points):

(5 points) Find the tangent plane to the surface \[f(x, y, z)=x^{2} y-x^{3}+y^{2}+z^{4} x y=-13\] at the point $(2,-1,1)$.
(5 points) Estimate $f(2.001,-0.99,1.1)$ by linear approximation.

Problem 28A.5 (10 points):

(5 points) Find the quadratic approximation $Q(x, y)$ of \[f(x, y)=5+x+y+x^{2}+3 y^{2}+\sin (x y)+e^{x}\] at $(x, y)=(0,0)$.
(5 points) Estimate the value of $f(0.001, 0.02)$ using quadratic approximation.

Problem 28A.6 (10 points):

(8 points) Classify the critical points of the function \[f(x, y)=x^{2}-y^{3}+2 x+3 y\] using the second derivative test.
(2 points) Does the function $f(x, y)$ have a global minimum or global maximum?

Problem 28A.7 (10 points):

Using the Lagrange optimization method, find the parameters $(x, y)$ for which the area of an arch \[f(x, y)=2 x^{2}+4 x y+3 y^{2}\] is minimal, while the perimeter \[g(x, y)=8 x+9 y=33\] is fixed.

Problem 28A.8 (10 points):

(5 points) Find the moment of inertia \[I=\iint_{G}(x^{2}+y^{2}) \,d y \,d x\] of the quarter $G=\{x^{2}+y^{2} \leq 1,\ x \geq 0,\ y \leq 0\}$.
(5 points) Evaluate the double integral \[\int_{1}^{e} \int_{\log (x)}^{1} \frac{y}{e^{y}-1} \,d y \,d x\] where $\log$ is the natural log as usual.

Problem 28A.9 (10 points):

Find the integral \[\iiint_{E} f(x, y, z) \,d z \,d y \,d x\] of the function \[f(x, y, z)=x+(x^{2}+y^{2}+z^{2})^{4}\] over the solid \[E=\left\{(x, y, z) \mid 1 \leq x^{2}+y^{2}+z^{2} \leq 4,\ z \geq 0\right\}.\]

Problem 28A.10 (10 points):

Find the surface area of \[r(x, y) = \begin{bmatrix} 2x\\ y\\ \frac{x^3}{3} + y \end{bmatrix}\] with $0 \leq x \leq 2$ and $0 \leq y \leq x^{3}$.

28.3 Second Hourly (Practice B)

Problem 28B.1 (10 points):

(4 points) You know the positive integer $n^{5}$ is odd. Prove that $n$ is odd.
(3 points) Prove or disprove: if $a$ and $b$ are irrational, then $a b$ is irrational.
(3 points) Prove or disprove: if $a$ and $b$ are irrational, then $a+b$ is irrational.

Problem 28B.2 (10 points, each sub problem is one point):

What is the name of the differential equation $f_{t}=f_{x x}$?
What assumptions need to hold so that $f_{x y}=f_{y x}$ is true?
The gradient $\nabla f(x_{0})$ has a relation to $f(x)=c$ with $c=f(x_{0})$. Which one?
The linear approximation of $f$ at $x_{0}$ is $L(x)=f(x_{0})+\cdots$. Complete the formula.
Assume $f$ has a maximum on $g=c$, then either $\nabla f=\lambda \nabla g$, $g=c$ holds or...
Which mathematician proved the switch the order of integration formula?
True or false: the gradient vector $\nabla f(x)$ is the same as $d f(x)$.
The equation $u_{t}+u u_{x}=u_{x x}$ is an example of a differential equation. We have seen two major types (each a three capital letter acronym). Which type is it?
What is the formula for the arc length of a curve $C$?
What is the integration factor $|d \phi|$ when going into polar coordinates?

Problem 28B.3 (10 points, 2 points for each sub-problem):

We see the level curves of a Morse function $f$. Only pick points $A$-$J$.

Which point is critical with discriminant $D=\operatorname{det}(d^{2} f)<0$.
At which point is $f_{x}>0$, $f_{y}=0$?
At which point is $f_{x}>0$, $f_{y}>0$?
Which $(x_{0}, y_{0})$ are critical points of $f$ when imposing the constraint $g(x, y)=y=y_{0}$?
Which $(x_{0}, y_{0})$ are critical points of $f$ when imposing the constraint $g(x, y)=x=x_{0}$?

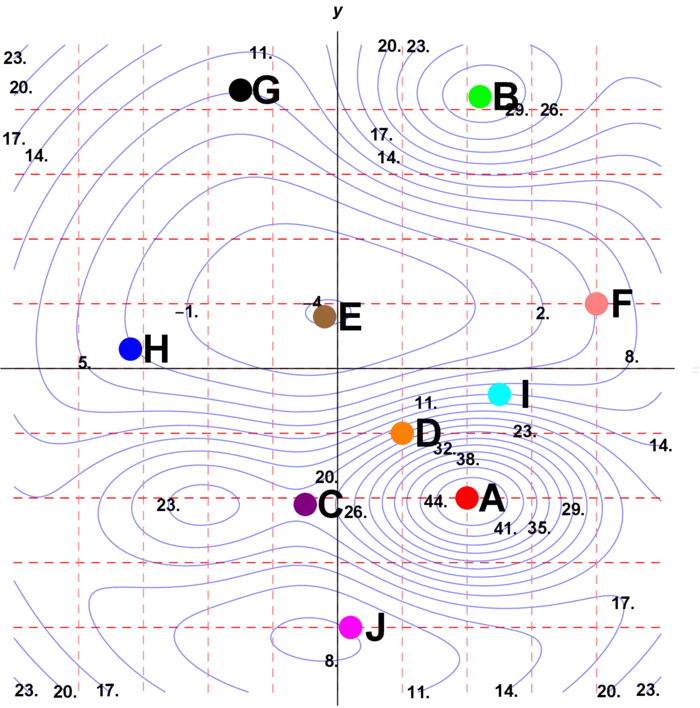
Problem 28B.4 (10 points):

(5 points) Find the tangent plane to the surface $x y z+x^{5} y+z=11$ at $(1,2,3)$.
(5 points) Near $(x, y)=(1,2)$, we can write $z=g(x, y)$. Find $g_{x}(1,2)$, $g_{y}(1,2)$.

Problem 28B.5 (10 points):

Find the quadratic approximation of \[f(x, y, z)=1+x+y^{2}+z^{3}+\sin (x y z)\] at $(0,0,0)$.
Estimate $f(0.01,0.03,0.05)$ using linear approximation.

Problem 28B.6 (10 points):

(8 points) Classify the critical points of the function \[f(x, y)=x^{12}+12 x^{2}+y^{12}+12 y^{2}\] using the second derivative test.
(2 points) Does $f$ have a global minimum? Does $f$ have a global maximum?

Problem 28B.7 (10 points):

On the top of a MIT building there is a radar dome in the form of a spherical cap. Insiders call it the "Death star" radar dome. We know that with the height $h$ and base radius $r$, we have volume and surface area given by $V=\pi r h^{2}-\pi h^{3} / 3$, $A=2 \pi r h=\pi$. This leads to the problem to extremize \[f(x, y)=x y^{2}-\frac{y^{3}}{3}\] under the constraint \[g(x, y)=2 x y=1.\] Find the minimum of $f$ on this constraint using the Lagrange method!

Problem 28B.8 (10 points):

Find \[\iint_{R} 5 /(x^{2}+y^{2}) \,d x \,d y\] where $R$ is the region $1 \leq x^{2}+y^{2} \leq 25$, $y^{2}>x^{2}$.

Problem 28B.9 (10 points):

Integrate $f(x, y, z)=z$ over the solid $E$ bound by \[\begin{aligned} & z=0 \\ & x=0 \\ & y=0 \end{aligned}\] and \[x+y+z=1.\]

Problem 28B.10 (10 points):

What is the surface area of the surface \[r(x, y) = \begin{bmatrix} 2y\\ x\\ \frac{y^3}{3} + x \end{bmatrix}\] with $0 \leq y \leq 2$ and $0 \leq x \leq y^{3}$?

28.4 Second Hourly

Problem 28.1 (10 points):

(3 points) Prove or disprove that the product of a rational and an irrational number is irrational.
(3 points) Prove or disprove that the product of two irrational numbers is irrational.
(2 points) Prove or disprove that the product of two numbers of the form $4 k-1$ is a number of the form $4 k-1$.
(2 points) Prove or disprove that the product of two numbers of the form $4 k+1$ is a number of the form $4 k+1$.

Problem 28.2 (10 points, each question is one point):

What is the name of the partial differential equation $f_{t}=f f_{x}$?
The series \[f(x)=\sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}=1-\frac{x^{2}}{2 !}+\frac{x^{4}}{4 !}-\frac{x^{6}}{6 !} + \cdots\] represents a function. Which one?
The implicit differentiation formula for $f(x, y, z(x))=1$ is $z_{x}(x)=\ldots \ldots$.
The problem to compute the value of $\zeta(s)=\sum_{n=1}^{\infty} n^{-s}$ for $s=2$ is called the $\ldots\ldots$ problem.
Is it possible that we have a Morse function on the $2$-sphere $x^{2}+y^{2}+z^{2}=1$ has $3$ maxima, $1$ minimum and $3$ saddle points?
Who proved that one can change the order of integration on a rectangle? The result is called the theorem.
You measure progress with a Morse function $f$ in a data space $\mathbb{R}^{n}$. You are located at a point which is not a critical point. In which direction do you have to change the parameters to make $f$ larger?
The function $f(x, t)=\sin (x+t)+\sin (x-t)$ is a solution of of one of the basic partial differential equations. Which one?
What is the distortion factor of the coordinate change \[r: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3},(x, y, z) \rightarrow(3 x, 4 y, 7 z)?\]
You are on Elysium, a torus shaped artificial habitat on which the height function of the hills is a Morse function. There are $5$ hills (maxima) and $2$ sinks (minima). How many saddle points are there on Elysium?

Problem 28.3 (10 points, each question is one point):

We see the level curves of a Morse function $f$. In every of the question, we pick exactly one point from $A$, $B$, $C$, $D$, $E$, $F$, $G$, $H$, $I$, $J$, $K$, $L$. Points might appear several times and some points might not appear.

Which point is a local maximum?
Which point is a local minimum?
Which point is a saddle point?
Which point is a local minima of $f$ under the constraint $g(x, y)=y=0$?
Which point is a local maxima of $f$ under the constraint $g(x, y)=y=0$?
At which point is $|\nabla f(x, y)|$ maximal among all the points?
At which point is $f_{x}(x, y)$ positive and $f_{y}(x, y)=0$?
At which point is $f_{y}(x, y)$ positive and $f_{x}(x, y)=0$?
At which point are both $f_{x}(x, y)$ and $f_{y}(x, y)$ positive?
At which point are both $f_{x}(x, y)$ and $f_{y}(x, y)$ negative?

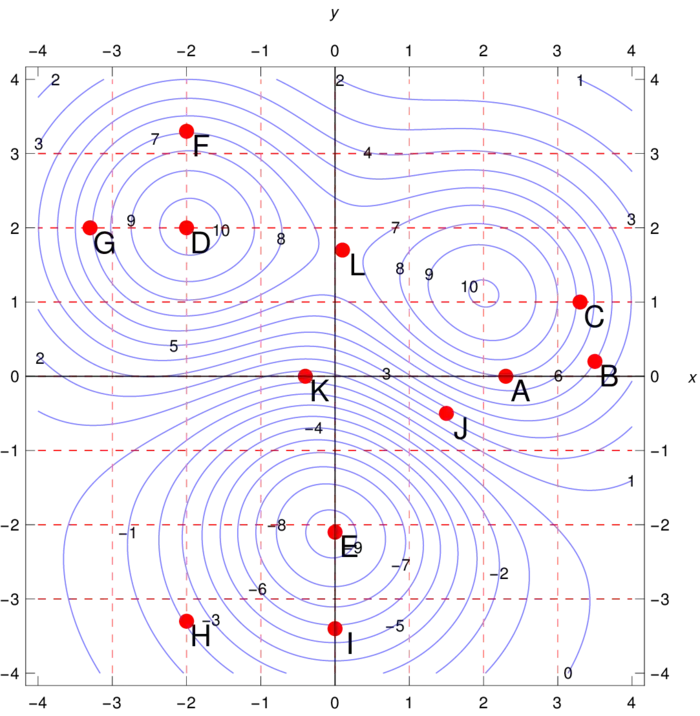
Problem 28.4 (10 points):

(5 points) Find the tangent hyper plane $a x+b y+c z+d w=e$ to the hyper surface \[f(x, y, z, w)=x y^{2} z^{2}+w=2\] at the point $(x_{0}, y_{0}, z_{0}, w_{0})=(2,-1,-1,0)$.
(5 points) Estimate $f(2.001,-0.9,-1.01,0.07)$ by linear approximation.

Problem 28.5 (10 points):

(6 points) Classify the critical points of the function \[f(x, y)=3-3 x+x^{2}-3 y+x y+y^{2}\] using the second derivative test.
(2 points) Does the function $f(x, y)$ have a global minimum?
(2 points) Does the function $f(x, y)$ have a global maximum?

Problem 28.6 (10 points):

(4 points) Find the quadratic approximation $Q(x, y)$ of the function \[f(x, y)=3-3 x+x^{2}-3 y+x y+y^{2}\] at $(x_{0}, y_{0})=(1,1)$. We have already seen this function in Problem 28.5).
(3 points) Is this function $f$ a Morse function?
(3 points) Estimate the value of $f(1.03,0.2)$ using quadratic approximation.

Problem 28.7 (10 points):

Using the Lagrange optimization method, find the parameters $(x, y)$ for which \[f(x, y)=3-3 x+x^{2}-3 y+x y+y^{2}\] is maximal or minimal under the constraint \[g(x, y)=x^{2}+y^{2}=2.\]

Problem 28.8 (10 points):

(5 points) Evaluate the integral \[I=\iint_{G} e^{x^{2}+y^{2}} \,d y \,d x\] of the annular region $G=\{1 \leq x^{2}+y^{2} \leq 4\}$.
(5 points) Evaluate the double integral \[\int_{1}^{3} \int_{0}^{9-x^{2}} \frac{y^{2}}{\sqrt{9-y}-1} \,d y \,d x.\]

Problem 28.9 (10 points):

Integrate

\[\iiint_{E}(x^{2}+y^{2}+z^{2})^{2} \,d z \,d y \,d x\] for \[E=\left\{(x, y, z) \mid 4 \leq x^{2}+y^{2}+z^{2} \leq 9,\ x^{2}+y^{2}

Problem 28.10 (10 points):

Compute the surface area of the surface \[r(u, v)=\left[\begin{array}{c} 2 v \cos (u) \\ 2 v \sin (u) \\ u^{2} \end{array}\right]\] over the region $R=\{u^{2}+v^{2} \leq 9\}$.

**Figure 1.** The surface in problem 10.