Review: Geometries and Fields

37.1 LECTURE

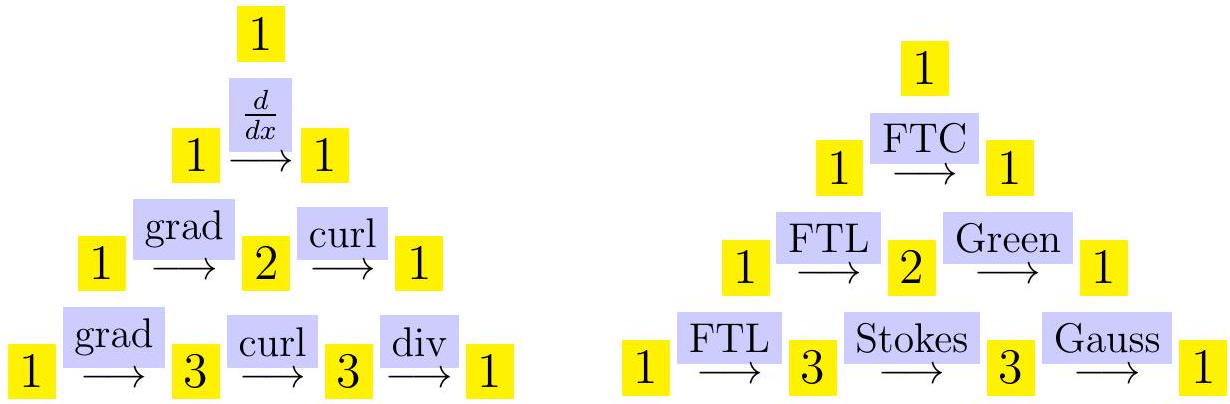
37.1.1 Classifying Integral Theorems by Dimension

The Integral theorems deal with geometries \(G\) and fields \(F\). Integration pairs them in the form of Stokes theorem \[\int_{G} d F=\int_{d G} F\] which involves the boundary \(d G\) of \(G\) and the exterior derivative \(d F\) of \(F\). One can classify the theorems by looking at the dimension \(n\) of the underlying space and the dimension \(m\) of the object \(G\). In dimension \(n\), there are \(n\) theorems:

37.1.2 Gradient and Line Integrals

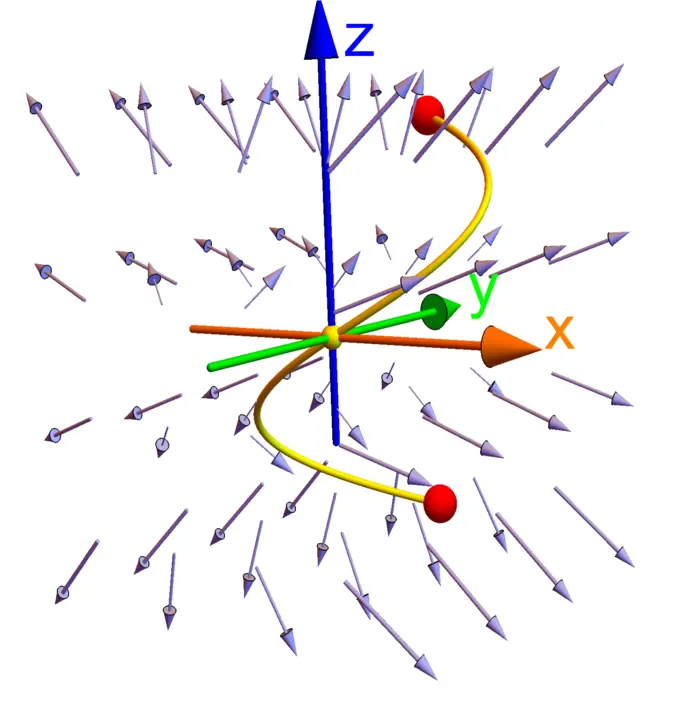
The Fundamental theorem of line integrals is a theorem about the gradient \(\nabla f\). It tells that if \(C\) is a curve going from \(A\) to \(B\) and \(f\) is a function (that is a \(0\)-form), then

In calculus we write the \(1\)-form as a column vector field \(\nabla f\). It actually is a \(1\)-form \(F=d f\), a field which attaches a row vector to every point. If the \(1\)-form is evaluated at \(r^{\prime}(t)\) one gets \(d f(r(t))(r^{\prime}(t))\) which is the matrix product. We integrate then the pull back of the \(1\)-form on the interval \([a, b]\). It is the switch from row vectors to column vectors which leads to the dot product \(\nabla f(r(t)) \cdot r^{\prime}(t)\). For closed curves, the line integral is zero. It follows also that integration is path independent.

37.1.3 Curls and Line Integrals: Green’s Connection

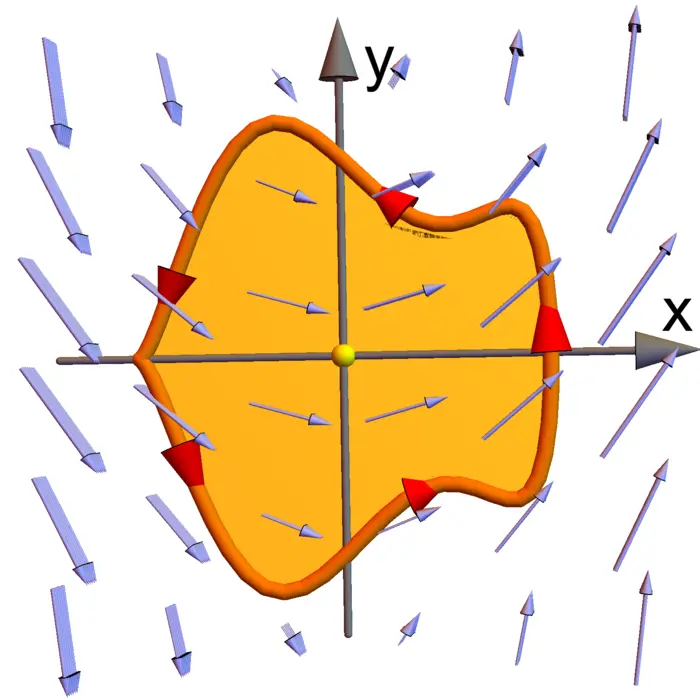
Green’s theorem tells that if \(G \subset \mathbb{R}^{2}\) is a region bound by a curve \(C\) having \(G\) to the left, then

In the language of forms, \(F=P \,d x+Q \,d y\) is a \(1\)-form and \[\begin{aligned} d F&=(P_{x} \,d x+P_{y} \,d y) \,d x+(Q_{x} \,d x+Q_{y} \,d y) \,d y\\ &=(Q_{x}-P_{y}) \,d x \,d y \end{aligned}\] is a \(2\)-form. We write this \(2\)-form \(d F\) as \(Q_{x}-P_{y}\) and treat it as a scalar function even so this is not the same as a \(0\)-form, which is a scalar function. If \(\operatorname{curl}(F)=0\) everywhere in \(\mathbb{R}^{2}\) then \(F\) is a gradient field.

37.1.4 Surfaces and Line Integrals

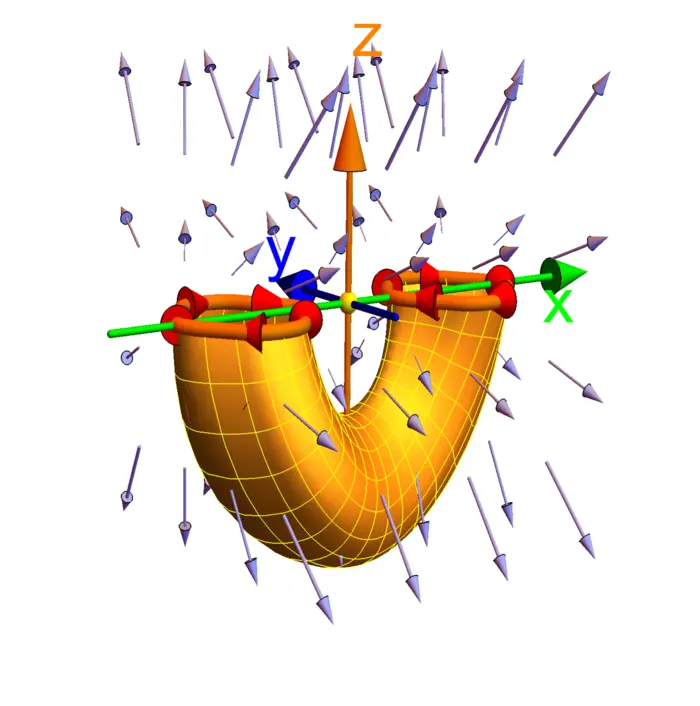
Stokes theorem tells that if \(S\) is a surface with boundary \(C\) oriented to have \(S\) to the left and \(F\) is a vector field, then

In the general frame work, the field \[F=P \,d x+Q \,d y+R \,d z\] is a \(1\)-form and the \(2\)-form \[\begin{aligned} d F&=(P_{x} \,d x+P_{y} \,d y+P_{z} \,d z) \,d x\\ &\quad +(Q_{x} \,d x+Q_{y} \,d y+Q_{z} \,d z) \,d y\\ &\quad +(R_{x} \,d x+R_{y} \,d y+R_{z} \,d z) \,d z\\ &=(Q_{x}-P_{y}) \,d x \,d y+(R_{y}-Q_{z}) \,d y \,d z+(P_{z}-R_{x}) \,d z \,d x \end{aligned}\] is written as a column vector field \[\operatorname{curl}(F)=[R_{y}-Q_{z}, P_{z}-R_{x}, Q_{x}-P_{y}]^{T}.\] To understand the flux integral, we need to see what a bilinear form like \(d x \,d y\) does on the pair of vectors \(r_{u}\), \(r_{v}\). In the case \(d x \,d y\) we have \[d x \,d y(r_{u}, r_{v})=x_{u} y_{v}-y_{u} x_{v}\] which is the third component of the cross product \(r_{u} \times r_{v}\) with \(r_{u}=[x_{u}, y_{u}, z_{u}]^{T}\). Integrating \(d F\) over \(S\) is the same as integrating the dot product of \(\operatorname{curl}(F) \cdot r_{u} \times r_{v}\). Stokes theorem implies that the flux of the curl of \(F\) only depends on the boundary of \(S\). In particular, the flux of the curl through a closed surface is zero because the boundary is empty.

37.1.5 Gauss Theorem: Sources, Sinks, and the Big Picture

Gauss theorem: if the surface \(S\) bounds a solid \(E\) in space, is oriented outwards, and \(F\) is a vector field, then

Gauss theorem deals with a \(2\)-form \[F=P \,d y \,d z+Q \,d z \,d x+R \,d x \,d y,\] but because a \(2\)-form has three components, we can write it as a vector field \(F=[P, Q, R]^{T}\). We have computed \[\begin{aligned} d F&=(P_{x} \,d x+P_{y} \,d y+Q_{z} \,d z) \,d y \,d z\\ &\quad +(Q_{x} \,d x+Q_{y} \,d y+Q_{z} \,d z) \,d z \,d x\\ &\quad +(R_{x} \,d x+R_{y} \,d y+R_{z} \,d z) \,d x \,d y, \end{aligned}\] where only the terms \[P_{x} \,d x \,d y \,d z+Q_{y} \,d y \,d z \,d x+R_{z} \,d z \,d x \,d y=(P_{x}+Q_{y}+R_{z}) \,d x \,d y \,d z\] survive which we associate again with the scalar function \(\operatorname{div}(F)=P_{x}+Q_{y}+R_{z}\). The integral of a \(3\)-form over a \(3\)-solid is the usual triple integral. For a divergence free vector field \(F\), the flux through a closed surface is zero. Divergence-free fields are also called incompressible or source free.

37.2 REMARKS

37.2.1 Triplet Trouble: Tensor Types Collide in 3D

We see why the \(3\)-dimensional case looks confusing at first. We have three theorems which look very different. This type of confusion is common in science: we put things in the same bucket which actually are different: it is only in \(3\) dimensions that \(1\)-forms and \(2\)-forms can be identified. Actually, more is mixed up: not only are \(1\)-forms and \(2\)-forms identified, they are also written as vector fields which are \(T_{0}^{1}\) tensor fields. From the tensor calculus point of view, we identify the three spaces \[T_{0}^{1}(E)=E, \quad T_{1}^{0}(E)=\Lambda^{1}(E)=E^{*}, \quad \text{and} \quad \Lambda^{2}(E) \subset T_{2}^{0}.\] While we can still always identify vector fields with \(1\)-forms, this identification in a general non-flat space will depend on the metric. In \(\mathbb{R}^{4}\), the \(2\)-forms have dimension \(6\) and can no more be written as a vector. One still does. The electro-magnetic \(F\) is a \(2\)-form in \(\mathbb{R}^{4}\) which we write as a pair of two time-dependent vector fields, the electric field \(E\) and the magnetic field \(B\).

37.2.2 Hilbert Space Harmonization: Merging Geometries and Fields

Geometries and fields are remarkably similar. On geometries, the boundary operation \(d\) satisfies \(d \circ d=0\). On fields the derivative operation \(d\) satisfies \(d \circ d=0\). "Geometries" as well as "fields" come with an orientation: \[r_{u} \times r_{v}=-r_{v} \times r_{u}, \quad d x \,d y=-d y \,d x.\] The operations \(d\) and \(d\) look different because calculus deals with smooth things like curves or surfaces leading to generalized functions. In quantum calculus they are thickened up and \(d\), \(d\) defined without limit. Fields and geometries then become indistinguishable elements in a Hilbert space. The exterior derivative \(d\) has as an adjoint \(d=d^{*}\) which is the boundary operator. It is a kind of quantum field theory as \(d\) generates while \(d^{*}\) destroys a "particle". \(d^{2}=d^{2}=0\) is a "Pauli exclusion".

37.2.3 Dual Forms and Jacobians: A Manifold-Field Marriage

We can spin this further: a \(\boldsymbol{m}\)-manifold \(S\) is the image of a parametrization \(r: G \subset \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\). The Jacobian \(d r\) is a dual \(\boldsymbol{m}\)-form, the exterior product of the \(m\) vectors \(d r_{u_{1}}\) up to \(d r_{u_{m}}\) (think of \(m\) column vectors attached to \(r(u) \in S\)). If we take a map \(s: S \subset \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) and look at \(F=d s\), we can think of it as a \(m\)-form \(F\) (think of \(m\) row vectors attached to each point \(x\) in \(\mathbb{R}^{n}\)). The map \(s\) defines \(m \times n\) Jacobian \(d s(x)\), while the Jacobian \(d r(u)\) is the \(n \times m\) matrix. Cauchy-Binet shows that the flux of \(F=d s\) through \(r(G)=S\) is the integral \[\int_{G} F=\int_{G} \operatorname{det}\big(d s(r(u)) \,d r(u)\big) \,d u=\int_{S} \operatorname{det}\big(d s(x) \,d r(s(x))\big).\] If \(s(r(u))=u\), then this is a geometric functional. So: geometries \(G\) can come from maps from a space \(A\) to a space \(B\), while fields \(F\) can come from maps from \(B\) to \(A\). The action integral \(\int_{G} F\) generalizes the Polyakov action \[\int_{G} \operatorname{det}(d r^{T} d r)=\int_{G}|d r|^{2},\] a case where \(F\) and \(G\) are dual meaning \(s(r(u))=u\).

37.3 PROTOTYPE EXAMPLES