Perpetual Motion Machines
Table of Contents
30.1 INTRODUCTION
30.1.1 Perpetual Motion: Dreams and Impossibility
Wouldn’t it be nice to have a machine which produces energy from nothing? Humans have dreamed about this for centuries. There is no mathematical proof that such a machine can not exist. It is an experimental fact that all isolated physical process we know preserve energy.1 In experiments, we see that all basic forces of nature are gradient fields. So, how come we can harvest energy from the wind force for example? Wind energy is driven by external sources, in particular the solar energy which heats up different parts of the earth surface. The sun energy comes from nuclear processes, mainly the fusion process.
30.1.2 Why Machines Fail: Unveiling the Mystery
It is a nice sport to come up with machines which seem to work or then to analyze a given machine which has been constructed and to find why it fails.
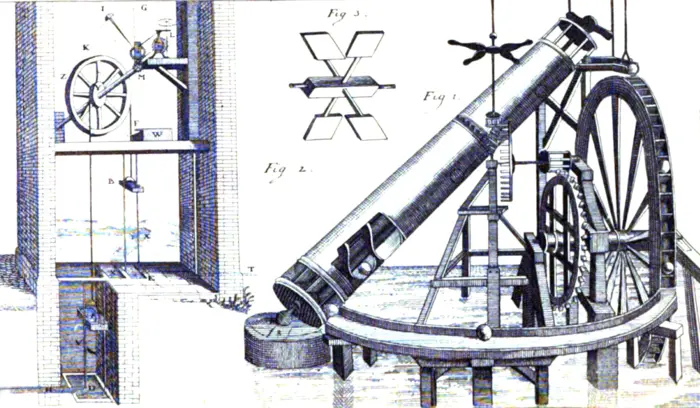
30.2 SEMINAR
30.2.1 The Water Pipe Machine
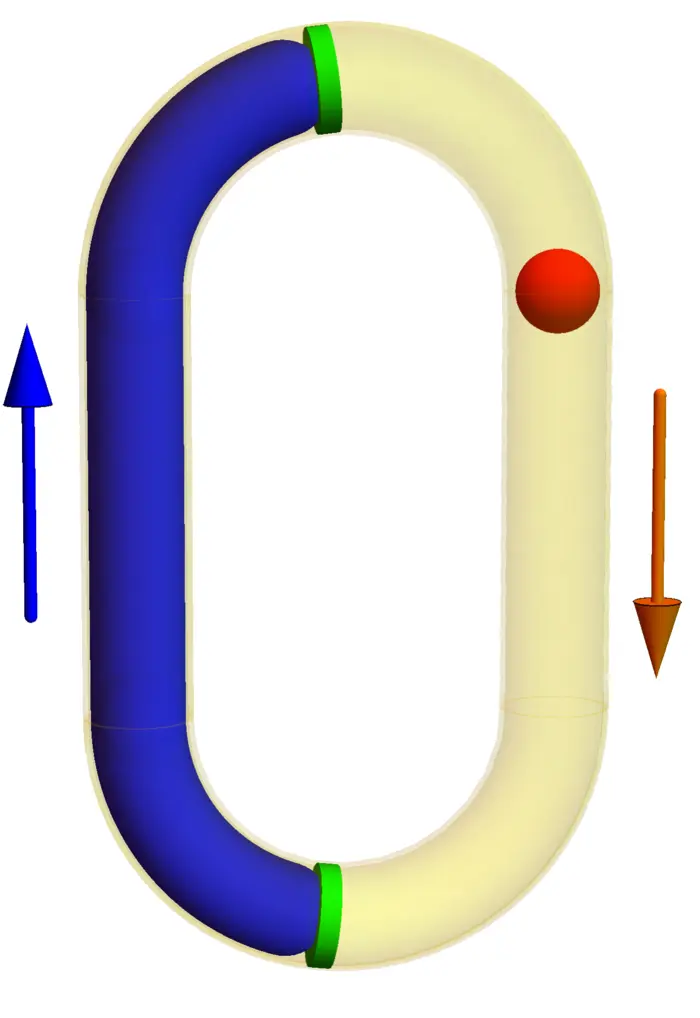
Our first machine is a circular pipe which is half filled with water. On the side without water, the gravitational force pulls a wooden ball down. On the water side, the buoyancy force pulls the ball up. Valves are in place so that the water stays in place.
Problem A: Analyse the pipe machine. You can assume that operating the valves uses arbitrary little energy and when opening one of the valves, the water stays in place.
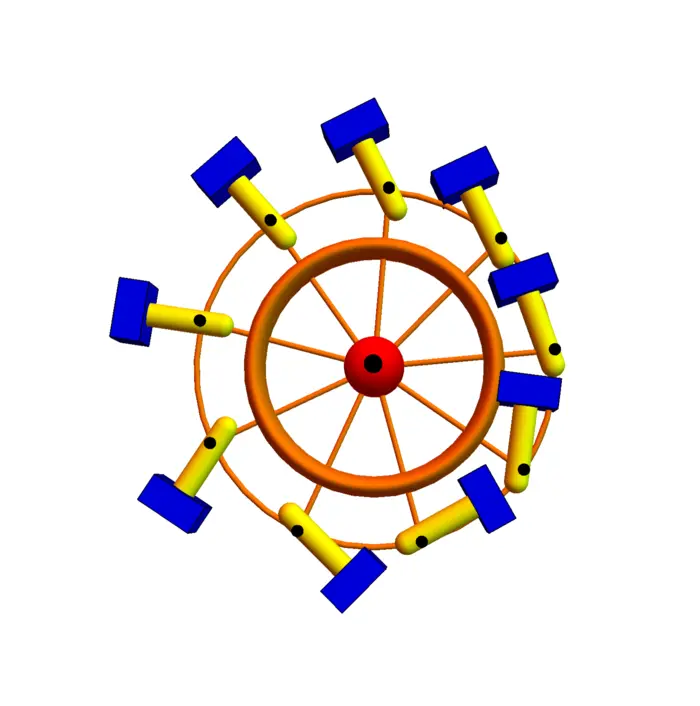
30.2.2 The Magnet Machine
An other class of machines uses magnets. Magnets are arranged in a circular way to produce a circular non-conservative force field in which a magnet is pushed forward.

Problem B: Analyze the magnet machine. Experiment with real magnets.
30.2.3 Line Integral Analysis
And then there are mechanical machines. Here is an example with weights.
Problem C: Analyze the hammer machine using line integrals using the gravitational potential \(f(x, y, z)=z\).
30.2.4 Challenging Gravity: The Capillary Effect
You all know that a sponge, a paper or a plant put into water lifts up the water using the capillary effect. In narrow spaces, this force can beat gravity.

Problem D: Why does the "capillary lifting machine" not work?
30.2.5 The Perpetual Motion Fallacy
Why are there no "perpetual motion machines"? There is no fundamental principle which forbids it. We could certainly produce a computer simulation of a world, where energy conservation fails. But it is like with "time machines". If such a machine would exist in our physical world, there would be serious dangers luring for a physicist who studies it. Benjamin Peirce refers in his book "A system of analytic mechanics" of 1855 to the "Antropic Principle": "Such a series of motions would receive the technical name of a ’perpetual motion’ by which is to be understood, that of a system which would constantly return to the same position, with an increase of power, unless a portion of the power were drawn off in some way and appropriated, if it were desired, to some species of work. A constitution of the fixed forces, such as that here supposed and in which a perpetual motion would possible, may not, perhaps, be incompatible with the unbounded power of the Creator; but, if it had been introduced into nature, it would have proved destructive to human belief, in the spiritual origin of force, and the necessity of a First Cause superior to matter, and would have subjected the grand plans of Divine benevolence to the will and caprice of man".
Problem E: Can you reformulate this "anthropic principle" in more modern terms? What could be the fate of a universe in which energy conservation does not hold in macroscopic physics?
30.2.6 Escher’s Illusory Forces
Non-conservative fields can also be generated by optical illusion as M.C. Escher did. The illusion suggests the existence of a force field which is not conservative. Can you figure out how Escher’s pictures "work"? This is part of the homework. Here is a last possible task for the seminar:
Problem F: Find some perpetual motion machine on the web (i.e. youtube). If you find something interesting, share with others. Why does it not work?
Problem G: Finally, if you have adventure spirit, Come up with a machine which actually works, get some seed money from investors or by crowd sourcing and then start production.

EXERCISES
Exercise 1. The force field \[F(x, y)=[-y /(x^{2}+y^{2}), x /(x^{2}+y^{2})]\] produces a nonconservative force. A body put near the vortex will spin around it. Check that that the field is a gradient field \(F=\nabla f\) with \(f=\arctan (y / x)\). Draw the level curves of \(f\), take a path \(r(t)=[\cos (t), \sin (t)]\) and verify that \[d / d t f(r(t))=\nabla f(r(t)) \cdot r^{\prime}(t)=1\] for all \(t\) so that \[\int_{0}^{2 \pi} \nabla f(r(t)) \cdot r^{\prime}(t) \,d t=2 \pi.\] Why does this not contradict the fundamental theorem?
Exercise 2. If \(H(x, y)\) is a function of two variables, then a curve \(r(t)=\) \([x(t), y(t)]\) satisfying \(x^{\prime}(t)=H_{y}(x, y)\) and \(y^{\prime}(t)=-H_{x}(x, y)\) is called a solution of the Hamiltonian system. The function \(H(x, y)\) is called the energy of the system. Verify that \(d / d t H(x(t), y(t))=0\) meaning that energy is conserved.
Exercise 3. Design a vector field \(F(x, y)=[P(x, y), Q(x, y)]\) which has the property such that for any closed curve \(C: r(t)\) in \(\{x^{2}+y^{2}>1\}\) winding once around the hole \(\{x^{2}+y^{2} \leq 1\}\), the line integral \(\int_{C} F(r(t)) \cdot r^{\prime}(t) \,d t\) is a multiple of \(6 \pi\). An example of a curve winding once around is \(r(t)=[2 \cos (t), 2 \sin (t)]\) with \(0 \leq t \leq 2 \pi\).
Exercise 4. A heat engine is a system that convert heat energy into mechanical energy. We have seen such a machine in class. How does it work?
Exercise 5. Explain the Escher waterfall illusion.
- Except for very short time, where virtual particles can appear and disappear in a short time frame.↩︎