Number Magic
Table of Contents
- 18.1 INTRODUCTION
- 18.2 SEMINAR
- 18.2.1 Calculus Hacks: Beyond Calculations
- 18.2.2 Newton’s Method for Roots: A Powerful Tool
- 18.2.3 Newton’s Method Takes a Complex Turn
- 18.2.4 Geometric Series Demystified
- 18.2.5 Convergence in Infinite Series
- 18.2.6 Unlocking Taylor Series with Infinite Series
- 18.2.7 Deriving Logarithms with Series
- 18.2.8 Exploring the Series at -1
- 18.2.9 Number Theory Meets Calculus
- 18.2.10 Zeta Function and the Riemann Hypothesis
- 18.2.11 The Euler Golden Key Identity
- 18.2.12 Exploring a Calculus-Based Equivalence to Goldbach
- EXERCISES
18.1 INTRODUCTION
18.1.1 Goldbach’s Challenge
One of the most famous open problems in mathematics is the Goldbach conjecture:
Every even integer larger than \(2\) is a sum of two primes.
Let \(g(n)\) denote the function which tells in how many ways we can write \(n\) as a sum of two primes. For example \(g(5)=2\), \(g(6)=1\) because \(5=2+3=3+2\) and \(g(6)=1\) because \(6+3+3\).
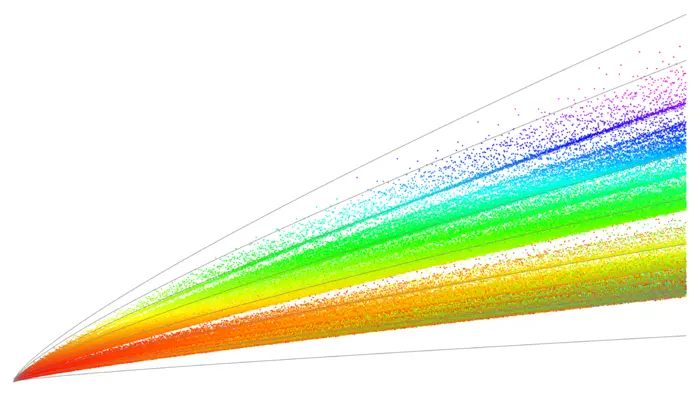
18.1.2 Goldbach Conjecture: Visualizing with Mathematica
Here is Mathematica code which allows to plot the comet, the graph of the function \(g\).
18.1.3 Cracking Goldbach with Calculus?
Why is this remarkable? It shows that computing the numbers \(f(n)\) could be done nicely using calculus by defining a function \(f\). Using Taylor’s theorem we can compute the entries \(g(n)\). The Goldbach conjecture is equivalent to \[\begin{aligned} g^{2 n}(0) \text { is nonzero for all } n \geq 1. \end{aligned}\] The only thing we would really need is to get a grip on the function \(f\). Unfortunately, nobody has seen how to write down the function \(f\) in terms of known functions. But it is not completely hopeless that there should not exist a modification \[f(x)=\sum_{p \text { prime }} a_{p} x^{p}\] with positive \(a_{p}\) such that \(f(x)\) is expressible using known functions. Also then, if \(g(x)=f(x)^{2}\) had positive even derivatives, Goldbach would follow.
18.2 SEMINAR
18.2.1 Calculus Hacks: Beyond Calculations
In this seminar, we see how calculus can help to compute things effectively and also hope to get insight into topics which are of more number theoretical nature. To find the cube root of \(10\) for example, we have \[10^{1 / 3} \sim 8^{1 / 3}+\frac{2}{3 \cdot 8^{2 / 3}}=2+\frac{2}{12}=2.1666 \ldots\] The actual value is \(2.15443\). We can also use linearization to find exact roots
Problem A: Find \((1030301)^{1 / 3}\) using linear approximation at \(x=1000000\).
18.2.2 Newton’s Method for Roots: A Powerful Tool
We could not mention the Newton method to find roots in class. It is a simple but effective iterative method. We can also do that to find roots. In order to find the cube root of \(9\) for example, we start with a first approximation like \(2\), then introduce the function \(f(x)=x^{3}-9\) for which we aim to find the root, then apply the Newton step \[T(x)=x-\frac{f(x)}{f^{\prime}(x)}.\] We have \(f^{\prime}(x)=3 x^{2}\) and so \(T(x)=x-(x^{3}-9) /(3 x^{2})\). This gives \(T(2)=25 / 12= 2.08333\). Already quite close to \(9^{1 / 3}=2.08008\).
18.2.3 Newton’s Method Takes a Complex Turn
There is an interesting story here when applying the Newton method in the complex plane. The function \(f(x)=x^{3}-9\) has exactly \(3\) roots in the complex plane. They are \(9^{1 / 3}\), \(9^{1 / 3} e^{i 2 \pi / 3}\) and \(9^{1 / 3} e^{i 4 \pi / 3}\). Check that these three numbers satisfy \(f(x)=0\)! Investigating the Newton method in the complex actually predated the Mandelbrot story. One can wonder what happens if you apply the Newton method with a given initial condition. The solution will end up in one of the three roots, but which ones? When drawing this, we see the Newton fractal. here is how you can plot the Newton fractal.1

18.2.4 Geometric Series Demystified
In the exam you have proven \(1+3+3^{2}+\cdots+3^{n-1}=\left(3^{n}-1\right) / 2\). This is a special case of the geometric series formula \[1+a+a^{2}+\cdots+a^{n}=\frac{1-a^{n+1}}{1-a}.\] Of course, we could also prove this formula by induction. Better do it directly:
Problem B: Verify the geometric series formula by multiplying with \(1-a\).
18.2.5 Convergence in Infinite Series
These were all finite sums but seeing the pattern allows us to take a limit and compute the infinite series:
Problem C: For which \(a\) is \(1+a+a^{2}+a^{3}+\cdots=\frac{1}{1-a}\) valid?
18.2.6 Unlocking Taylor Series with Infinite Series
The Taylor series of a nice function is \(f(x)=\sum_{k=0}^{\infty} f^{(k)}(0) x^{k}\). Having just looked at C) can answer the trick question:
Problem D: What is the Taylor series of \(f(x)=\frac{1}{(1-x)}\) at \(x_{0}=0\)?
18.2.7 Deriving Logarithms with Series
How can you get from the last exercise the following identity?
Problem E: \(-\log (1-x)=x+\frac{x^{2}}{2}+\frac{x^{3}}{3}+\frac{x^{4}}{4}+\cdots\)
18.2.8 Exploring the Series at -1
Now lets see what happens at \(x=-1\).
Problem F: Use E to see what happens for \(x=-1\).
18.2.9 Number Theory Meets Calculus
How come that great number theorists like Leonard Euler or Godfrey Hardy were also masters in calculus? The reason is that many results of number theoretic nature have intimate relations with calculus. Lets look at the following problem:
Problem G: What is the value of the Leibniz series \[1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots\]
Hint: compute first the Taylor series of \(f(x)=\arctan (x)\) using the Taylor series of \(1 /(1+x^{2})\) (the later is a geometric series), then evaluate \(f\) at \(x=1\).
18.2.10 Zeta Function and the Riemann Hypothesis
\[\operatorname{Li}_{s}(x)=\sum_{n=1}^{\infty} \frac{x^{n}}{n^{s}}=x+\frac{x^{2}}{2^{s}}+\frac{x^{3}}{3^{s}}+\cdots\] is called the poly logarithm function. For \(s=0\) it is Problem D, for \(s=1\) it is problem E. While in calculus, we might be more interested in the function as a function of \(x\), number theorists are more interested in the function as a function of \(s\) and \(s\) is complex. In the case \(x=1\), the function \(L i_{s}(x)\) is the Riemann zeta function \(\zeta(s)=\sum_{k=1}^{\infty} \frac{1}{k^{s}}\).
Problem H: What does the Riemann hypothesis say?
The Euler golden key relates \(\zeta\) with primes:
Theorem 1. \(\zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^{s}}=\prod_{p \text { prime }}\big(1-\frac{1}{p^{s}}\big)^{-1}\).
18.2.11 The Euler Golden Key Identity
Problem I: Verify the Euler golden key identity.
First verify (maybe look at Problem C) that for a single prime \(p\) \[\frac{1}{1-\frac{1}{p^{s}}}=1+\frac{1}{p^{s}}+\frac{1}{p^{2 s}}+\frac{1}{p^{3 s}}+\cdots\] which is the sum over all \(\frac{1}{n^{s}}\), where \(n\) has only prime factors \(p\). Then look at the product of these for two primes \(p\), \(q\) and see that this is the sum over all \(\frac{1}{n^{s}}\) where \(n\) has only prime factors \(p\) and \(q\).
18.2.12 Exploring a Calculus-Based Equivalence to Goldbach
Lets come back to the topic of the introduction. Remember that the Goldbach conjecture tells that every even number larger than \(2\) is the sum of two primes. What is the relation with calculus? Define \(g(x)=(f(x))^{2}\) with \[f(x)=\sum_{p} \frac{x^{p}}{p !}=\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}+\frac{x^{7}}{7 !}+\cdots\] For the following, try to verify this carefully by showing both directions. If a statement \(A\), \(B\) are equivalent then this means that we have to show two things. We have to verify that \(A \implies B\) and \(B \implies A\).
Problem J: Goldbach is equivalent to \(g^{(n)}(x)>0\) for all even \(n>2\).
EXERCISES
Exercise 1. The weak Goldbach conjecture claims that every integer larger or equal than 6 is a sum of three primes. Check this for \(n=\) \(6,7,8,9,10,11, \ldots\). The theorem is proven since 2015 (will appear in the Annals of mathematics). Use a computer to draw a picture of the weak Goldbach comet.
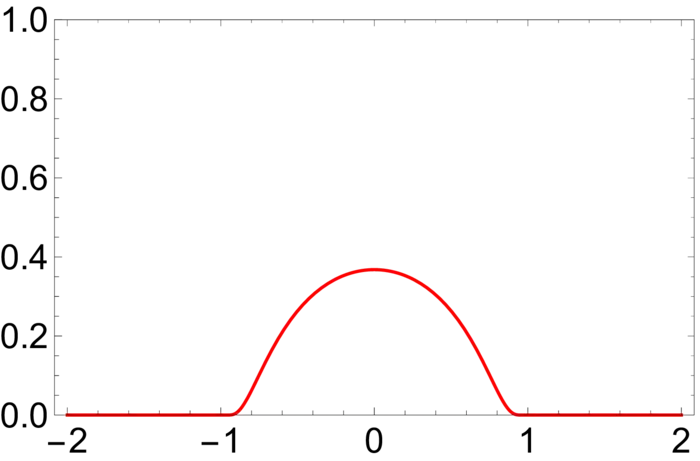
Exercise 2. The function \(f\) defined by \(f(x)=e^{-1 / x}\) for \(x>0\) and \(0\) for \(x \leq 0\) is smooth and that all derivatives at \(0\) are zero. Check \(f^{\prime}(0), f^{\prime \prime}(0), f^{\prime \prime \prime}(0)=0\). Conclude that there are smooth functions for which the Taylor expansion does not work. Check then that is \(b(x)=\) \(f(r^{2}-|x|^{2})\) a "bump function" (see figure 18.3). First define what a "bump function" is.
Exercise 3. The series \[\zeta(2)=1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\cdots\] a long history. Research it a bit. Especially: What is the value of \(\zeta(2)\). Who found this problem first? What is the name of the problem? Now look at \(\zeta(3)\). Is there like for \(\zeta(2)\) an explicit formula? Does one know whether \(\zeta(3)\) is rational or not?
Exercise 4. By looking it up, give an explanation why it makes sense that \[\zeta(-1)=1+2+3+4+\cdots\] can be assigned a finite value. You can also look up its value \(-1 / 12\) with Mathematica Zeta[-1]. How is such a finite value possible? In your explanation, we just want to know which field of mathematics is involved and what the idea is to define \(\zeta(s)\) also for \(s=-1\), a point where the sum diverges. Finally, what are the values \[\zeta(-2), \zeta(-3), \zeta(-4), \zeta(-5), \ldots \zeta(-9).\] The last one is \[\zeta(-9)=1^{9}+2^{9}+3^{9}+4^{9}+\cdots\]
Exercise 5. You can practice computing square roots of numbers between \(1\) and \(100\) by linear approximation in your head. For example, if somebody asks you to compute \(\sqrt{20}\) you would immediately tell \(4+4 /(2 \cdot 4)=4.5\). The actual result is \(4.472 \ldots\) You you could also get \(5-5 /(2 \cdot 5)=4.5\). Find another non-square integer in \(1\) to \(100\) for which these two estimates agree. (There are a couple of them).
- T is define a second time because we do not want to differentiate f symbolically in each evaluation of T and N[] forces floating point arithmetic.↩︎