Island Mathematics

 

21.1 INTRODUCTION

21.1.1 Modeling Spectacle Island’s Topography

We are on spectacle island, near the Boston Harbor and decide to understand the function \(f(x, y)\) which gives the height at a position \((x, y)\). The island has once been an "out of sight, out of mind" place occupied by a horse rendering plant (morphing horses to leather and fertilizers) and (related) a grease reclamation facility and a garbage disposal area. Barf! In the 1960ies, there came a renewal, to clean up the island and reclaim and reshape the island into a public park. It has now \(5\) miles of trails and fine beaches. The island has become an example of how to recreate a sustainable open space.

Figure 1. Spectacle island in Boston has two local hills and a saddle point of the height function \(f(x, y)\). We assume that the function is \(0\) at the beaches. Can one say something general about the maxima, the minima and saddle points of an island? In this case we have two maxima and one saddle point.

21.1.2 Optimizing Island Coastlines with Calculus

When we were looking for maxima and minima this week, we were not concerned so much how many critical points there are or which combinations of critical points can occur. It turns out this is a very exciting topic. An other theme we can explore while vising an island is to look at the relation between its area and its circumference (the length of the beaches). If the area is fixed, how short or how long can the total beach area become? It turns out that this is an infinite dimensional Lagrange problem but we can explore this also in finite dimensions when looking at polygonal island. We use the topic here to explore a bit some related areas to calculus.

Figure 2. An island with \(4\) mountain peaks, one sink and \(4\) mountain passes. The island theorem assuring that \(\mathrm{peaks} + \mathrm{sinks} - \mathrm{passes} =1\) is satisfied.

21.2 MAXIMIZING AREA

21.2.1 The Isoperimetric Problem: Islands and Optimal Shapes

An "island" a region in the plane \(\mathbb{R}^{2}\) which is bound by a simple closed curve \(C\) which is continuous everywhere and differentiable everywhere except at a finite set of points. We allow for exceptions for continuity to allow simple polygons. Which island does have the maximal area if the length of the boundary is fixed? This is called the isoperimetric problem. If we look at the problem restricted to polygons with a fixed number \(n\) of vertices, we have a nice finite dimensional Lagrange problem.

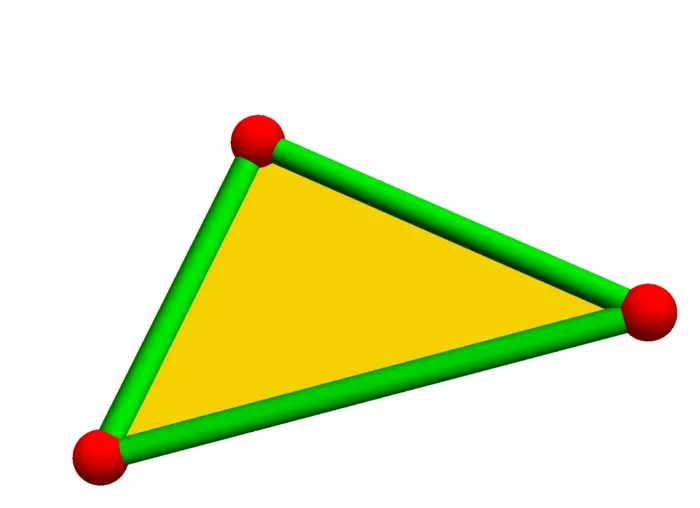
21.2.2 Triangle’s Max Area

Let us look at a triangular island \(T(x, y)\) with vertices \((-1,0)\), \((1,0)\), \((x, y)\).

Problem A: Assume the circumference \[g(x, y)=1+\sqrt{(x+1)^{2}+y^{2}}+\sqrt{(x-1)^{2}+y^{2}}\] of the triangle is \(3\). What is the maximal area \(f(x, y)=y / 2\) we can get? Set up the Lagrange equations and solve them.

21.2.3 Exploring the Locus of Points with a Fixed Distance Sum

Here is a related problem from good old Euclidean geometry. If you should not know, look up "string method pins".

Problem B: What points \((x, y)\) in the plane satisfy \(g(x, y)=3\)? This means, which points of the plane have the property that the sum of the distances to the two points is constant?

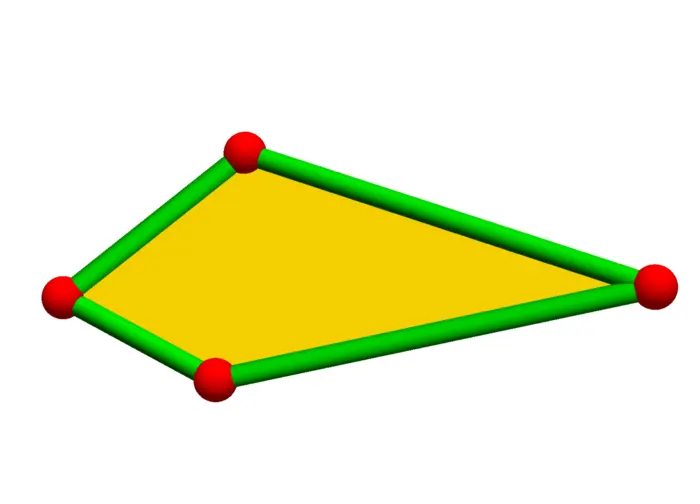
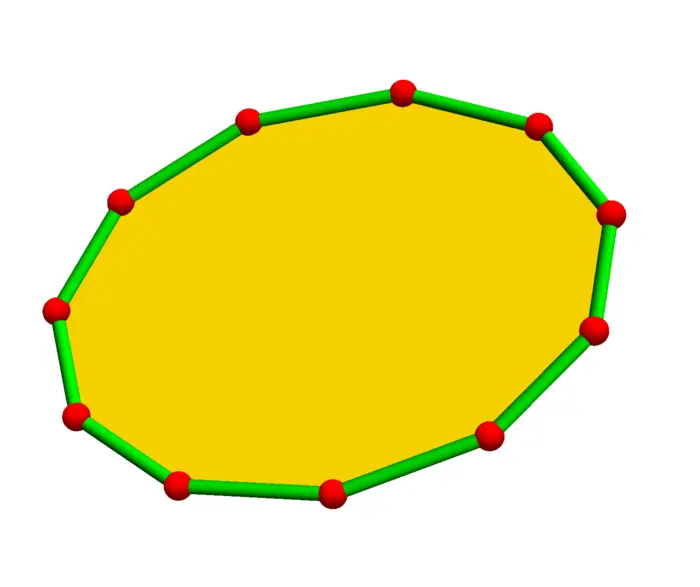
21.2.4 Connecting Triangles and Regular Polygons

Solving the problem to find the \(n\)-gon with maximal area is a messy Lagrange problem. It can be done by a computer but there is a more elegant way:

Problem C: Use the computation in problem A to show that in order to get maximal area for the triangle with vertices \(\ldots, P, Q, R, \ldots\) in a row, the distance between \({P}\) and \({Q}\) has to be the same as the distance between \({Q}\) and \({R}\).

Problem D: Conclude that a polygon with \({n}\) vertices and maximal area must be a regular polygon.

21.2.5 Reflecting the Way

You are on a treasure island \(G\) and have two locations \(A\), \(C\) in \(G\). You need to get from \(A\) to \(C\) but want to reach a point on the beach. It turns out that the solution is the billiard law of reflection at the boundary. Look at a triangle \(A B C\), replace the curve with the tangent curve \(L\) at \(B\). Reflect \(C\) at \(L\) to get a point \(C^{\prime}\). The path is shortest if the path \(A B C\) has the same length than the path connecting \(A\) with \(C^{\prime}\) directly.

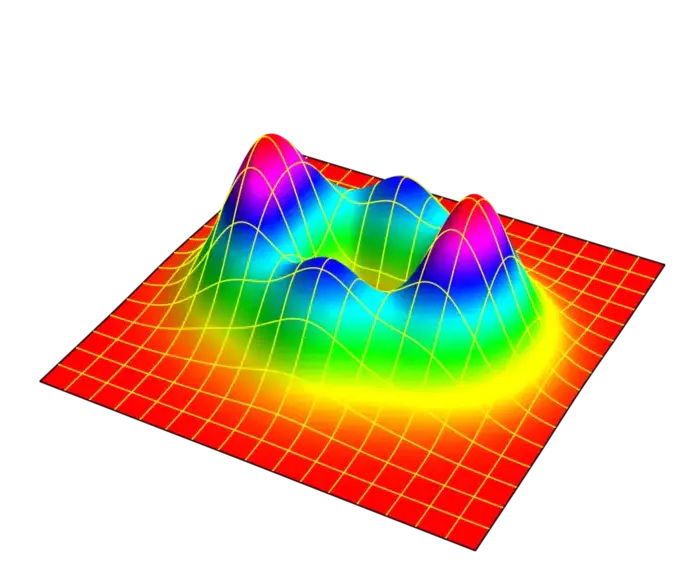
Figure 3. What polygon with fixed circumference has maximal area?

21.3 Mountains, Sinks and Mountain Passes

21.3.1 Exploring the Poincaré-Hopf Theorem with Peaks and Pits

The next time you are cast away on an island, count the number \(m\) of mountain peaks, the number \(s\) of sinks and the number \(p\) of mountain passes. Make some experiments. You notice the following rule which is known as a special case of the Poincaré-Hopf theorem:

Theorem 1. \(\mathrm{maxima} + \mathrm{minima} - \mathrm{saddles} =1\).

Problem F: Find an example where this equality holds, in which we have \(\mathrm{maxima}=3\), \(\mathrm{minima} =1\) and \(\mathrm{saddles} =3\).

21.3.2 Island Theorem on Atoll Rings

If you want to challenge yourself, see whether you can prove the island theorem by deformation. (This is probably too hard. Just enjoy the struggle!)

Problem G: Assume now that our island is an atoll, a ring shaped reef. By looking at examples, what is the island number \(\mathrm{maxima} + \mathrm{minima} - \mathrm{saddles}\) on an atoll?

Figure 4. First an island with \(2\) mountain peaks and with \(1\) mountain pass. Then an island with \(3\) mountain peaks and \(2\) mountain passes. We see \(\mathrm{maxima} + \mathrm{minima} - \mathrm{saddles} =1\).
Figure 5. The Atafu atoll. Picture by NASA Johnson Space Center, 2009.

Figure 6. If we place a surface \(S: g=c\) in space and look at the restriction of a function \(f(x, y, z)\) on \(S\), we solve a Lagrange problem. In a Morse situation, the numbers \(\mathrm{maxima} + \mathrm{minima} - \mathrm{saddles}\) add up to a number which only depends on the number of holes.

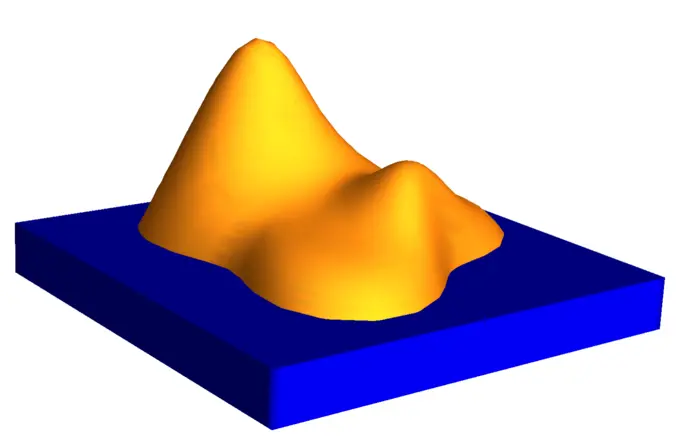
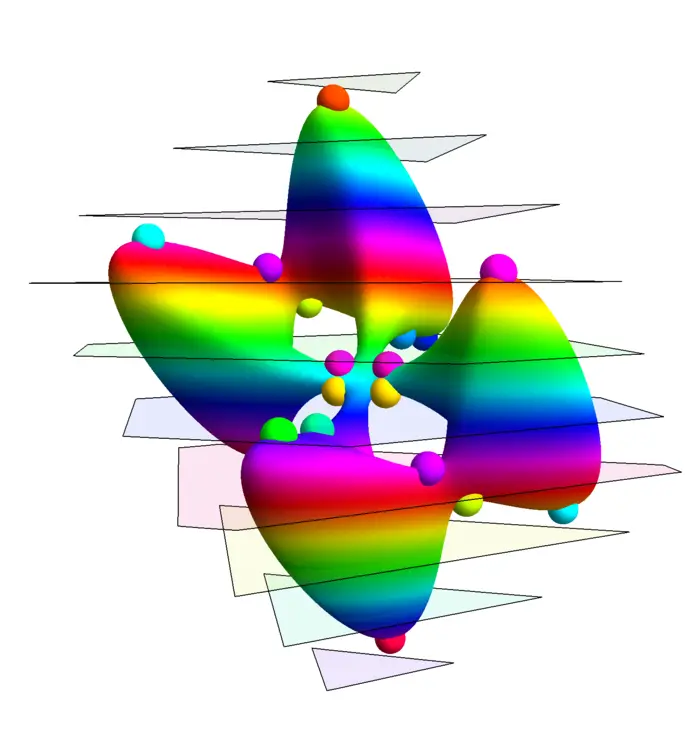
21.3.3 One-Dimensional Island Theorem

Let us look at the one-dimensional case, where we prove things easier. Assume the island is the interval \([a, b]\). Let \(f\) be a smooth function on \([a, b]\) which has the property that \(f\) is zero for \(x \geq b\) and for \(x \leq a\). We look at critical points of \(f\) in the interior \((a, b)\) which are Morse, (meaning \(f^{\prime \prime}(x) \neq 0\) at critical points), so that we only have only local maxima and minima as critical points. Let \(m\) be the number of maxima and \(s\) the number of minima (sinks). In order to prevent the island to be flooded, we also assume that the function \(f\) is positive for \(x>a\), close to \(a\) and \(x close to \(b\).

Theorem 2. \(\mathrm{maxima} - \mathrm{minima} =1\).

Problem H: Verify that there is an odd number of critical points for a Morse function \(f\) which has as a support a finite interval \([a, b]\).

Figure 7. One-dimensional islands.

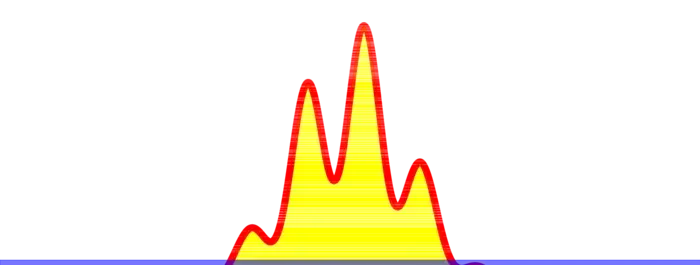
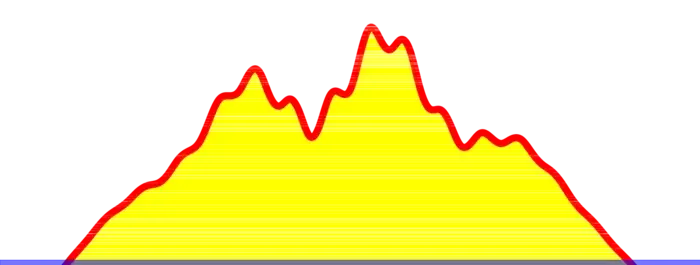
Problem I: Use a deformation argument to show that if there are \(2 k+ 1\) critical points, we can reduce them to \(2 k-1\) by merging a pair of neighboring maxima and minima.

EXERCISES

Exercise 1. Assume \(f: \mathbb{R} \rightarrow \mathbb{R}\) is a single variable Morse function on a circle. What is the relation between the number \(m\) of maxima on \([0,2 \pi)\) and the number of minima on \([0,2 \pi)\). Prove your statement.
Hint: verify that for a Morse function, it is not possible that two maxima are adjacent.

Exercise 2. If we look at maxima, minima and saddle points for a Morse function \(f(x, y)\) defined on a sphere, find the island number \(\mathrm{maxima} + \mathrm{minima} - \mathrm{saddles}\) there.

Exercise 3. If we look at maxima, minima and saddle points for a function \(f(x, y)\) defined on a doughnut. By looking at examples, find the island number \(\mathrm{maxima} + \mathrm{minima} - \mathrm{saddles}\) there.

Exercise 4. If we look at maxima, minima and saddle points on a brezel with two holes. Remember that you have constructed such a shape. By looking at examples, what is the island number \(\mathrm{maxima} + \mathrm{minima} - \mathrm{saddles}\) there? The simplest situation is if the function is linear in \(\mathbb{R}^{3}\).

Exercise 5. Describe how to build a concrete function \(f(x, y)\) of two variables which has two maxima and no minimum and no saddle point. (This is not possible on an island by the island theorem. It is possible however in the plane but such a function is not easy to describe. Discuss strategies with each other.)