Intuition
Table of Contents
- 9.1 INTRODUCTION
- 9.2 SEMINAR
- 9.2.1 Intuition in Historical Perspective
- 9.2.2 The Role of Intuition in Mathematics
- 9.2.3 Misleading Nature of Intuition
- 9.2.4 Defining Continuity Beyond Intuition
- 9.2.5 Challenging Our Intuitive Understanding
- 9.2.6 The Circumference of a Circle Revisited
- 9.2.7 Arc Length of Continuous Curves
- 9.2.8 Challenging Continuous Curves
- 9.2.9 The Devil’s Comb
- 9.2.10 Continuity and Differentiability
- 9.2.11 Weierstrass Function
- 9.2.12 The Challenge of Morley’s Theorem
- 9.2.13 Continuity of \(x\sin(1/x)\): A Closer Look
- EXERCISES
9.1 INTRODUCTION

9.1.1 The Essence of Intuition
Intuition is a mysterious notion in psychology. Ask a different school of psychology or go to a different culture and intuition will be understood in different ways. It is sometimes even linked to spirituality or religion. In mathematics, good intuition is usually thought of as the ability to "gain insight" or "see structures", sometimes an ability to be "creative". One attempt for definition is "understanding without conscious reasoning". Intuition can also be dangerous. An intuitive argument is not a proof for example, even if it might lead to a rigorous proof eventually. Extremely intuitive thinkers are sometimes also self-delusional. This is illustrated by the existence of extremely intuitive proofs of major open problems, but they are usually simply wrong.
9.1.2 Mathematical Intuition
What is intuition then? René Descartes tried to formulate it in his treatise "Rules for the Direction of the mind" written between 1619 and 1628. Rule 12 in that document tells "Finally we ought to employ all the help of understanding, imagination, sense and memory, first for the purpose of having a distinct intuition of simple propositions". For Descartes therefore, intuition has various components including understanding, imagination, sense and memory. This is a rather modern notion. A computer scientist can argue that computers already can be intuitive: the proof is by evidence only but we have seen in chess for example that computers have surpassed any human chess player. The last attempts by world chess champions to win against a machine failed. Since then, human-machine chess matches are all handicap variants, where the human is given a substantial advantage. And chess is a game where intuition is important.1
9.2 SEMINAR
9.2.1 Intuition in Historical Perspective
Despite all what has been said in the introduction, it is important in mathematics to gain "intuition" about objects, about definitions and about theorems and proofs. One way to see intuition is to see it as a mnemonic device which allows to understand things in a way which is better to remember. It also gives us pointers where we have to be careful. Non-intuitive results can also lead to intuition in other areas. An example from probability theory is the non-intuitive result that if you have a class of \(23\) students, the probability that two have the same birthday is more than a half. This is the birthday paradox. Indeed, the probability that none of them has the same birthday is \[(365 / 365)(364 / 365) \cdots (343 / 365)=0.4927.\] Now, once you have seen this, you have gained intuition about conincidences. They happen much more than we believe is reasonable. We can now take this to our advantage and design algorithms which gives us a result if two events collide. This has been used in cryptology for example. We can design algorithms which can pick a lock much faster than we believe is possible.2
9.2.2 The Role of Intuition in Mathematics
Now, rather than telling how to get intuition, it is maybe better to look at cases where intuition fails. This can then turned around and allows us to elevate our intuitive understanding. We will illustrate pitfalls with intuition by showing that intuitive notions can also mislead. We can state "false theorems" which we would believe to be true but which are false. We start with the notion of "continuity" for which an intuitive definition tells: we can "draw the graph of a continuous function without having to lift the pen". Of course, we can not work with this definition to prove theorems. It is a good intuitive notion although and provides some sort of "proto understanding". If you want to probe your notion of understanding about continuity, ask yourself whether the function \(f(x)=x \sin (1 / x)\) is continuous or not everywhere.
9.2.3 Misleading Nature of Intuition
Starting with Cauchy and pushed heavily by Weierstrass, continuity is defined precisely using the infamous \(\epsilon-\delta\) definition: \(f\) is continuous at \(x\), if for every \(\epsilon>0\) there exists \(\delta>0\) such that if \(|x-y| \leq \delta\), then \(|f(x)-f(y)| \leq \epsilon\). Using more fancy mathematical quantifier notation \(\forall\) (for all) and \(\exists\) (exists) and \(\Rightarrow\) (implies) and \(\epsilon\) (is element of) you can impress your friends (and annoy readers and graders) by writing \[\boxed{\forall \epsilon>0\, \exists \delta>0\, \forall y \in[a, b], |x-y| \leq \delta \Rightarrow|f(x)-f(y)| \leq \epsilon}\] The fact that his definition is not intuitive at all and that most students just learn this "epsilontic" by intimidation is illustrated by the following variation by Ed Nelson3 We make it our first exercise:
Problem A: What does the following statement mean?
\[\boxed{\forall \delta>0\, \exists \epsilon>0\, \forall y \in[a, b], |x-y| \leq \delta \Rightarrow|f(x)-f(y)| \leq \epsilon}\]
9.2.4 Defining Continuity Beyond Intuition
In the Monday lecture we have seen how a polygonal approximation of a curve allows to compute the arc length of a curve. Here is a first "anti-theorem". Your task is to figure out what is wrong.
9.2.5 Challenging Our Intuitive Understanding
We compute the circumference of a circle by a polygonal approximation. The following statement uses the intuition that if a polygon is close to a curve, then its length is close to the curve:
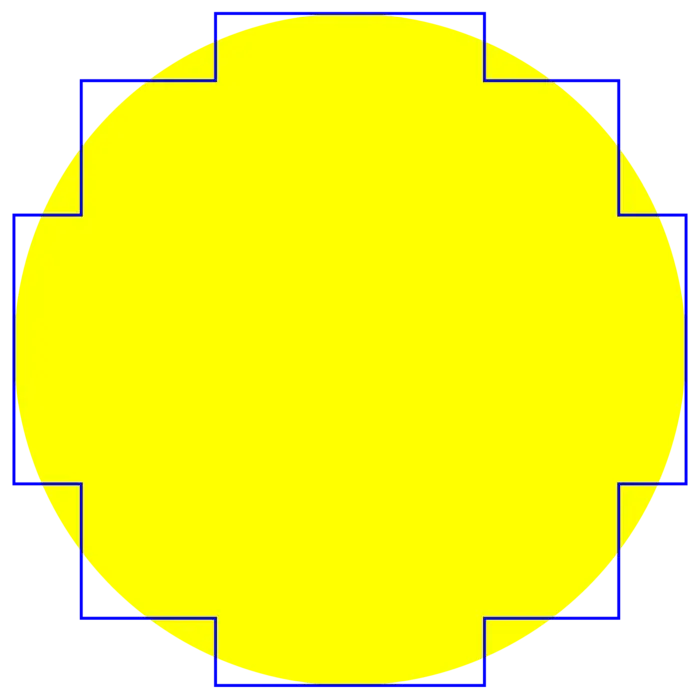



9.2.6 The Circumference of a Circle Revisited
This leads to the following anti-theorem:4 A continuous planar curve is a function \(t \rightarrow r(t)=[x(t), y(t)]\), where both functions \(x(t), y(t)\) are continuous functions.
False Theorem: The circumference of the unit circle is \(8\).
Problem B: What is wrong with the argumentation?
9.2.7 Arc Length of Continuous Curves
We could also think that the arc length of a continuous curve is finite.
False Theorem: The arc length of a continuous curve is finite.




Problem C: Find a formula for the length of the \(k\)’th Koch curve approximation if initially, the triangle has side length \(1\).
9.2.8 Challenging Continuous Curves
If a curve \(t \rightarrow r(t)=[x(t), y(t)]\) has the property that \(x(t)\) and \(y(t)\) stay bounded and have no jump discontinuities, we would think that the curve is continuous.
False Theorem: A bounded curve without jumps is continuous.
9.2.9 The Devil’s Comb
A counter example is the devil comb \(r(t)=[t, \sin (1 / t)]\) for \(t \in[0,1]\). It does not have a jump discontinuity and it is bounded. The function is not defined at \(t=0\) but we can define \(r(0)=[0,0]\) to make it defined anywhere on \([0,1]\).
Problem D: Why is this function \(r(t)\) not continuous at \(t=0\)?
9.2.10 Continuity and Differentiability
Finally, we could think:
False Theorem: A continuous function is differentiable at some point.
9.2.11 Weierstrass Function
A counter example was given by Weierstrass. It is called the Weierstrass function. G.H. Hardy proved in 1916 that the function \[f(x)=\sum_{n=1}^{\infty} a^{-n} \cos \left(a^{n} x\right)\] does not have any point of differentiability if \(a>1\).
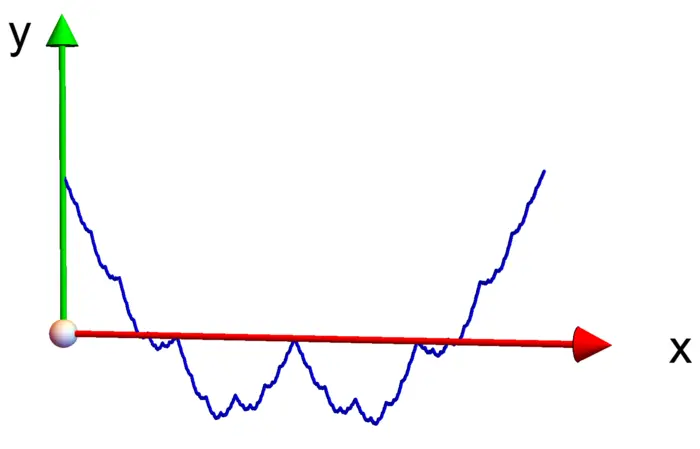
Problem E: Show that \(f(x)=\sum_{n=1}^{\infty} 2^{-n} \cos \left(2^{n} x\right) \in[-1,1]\).
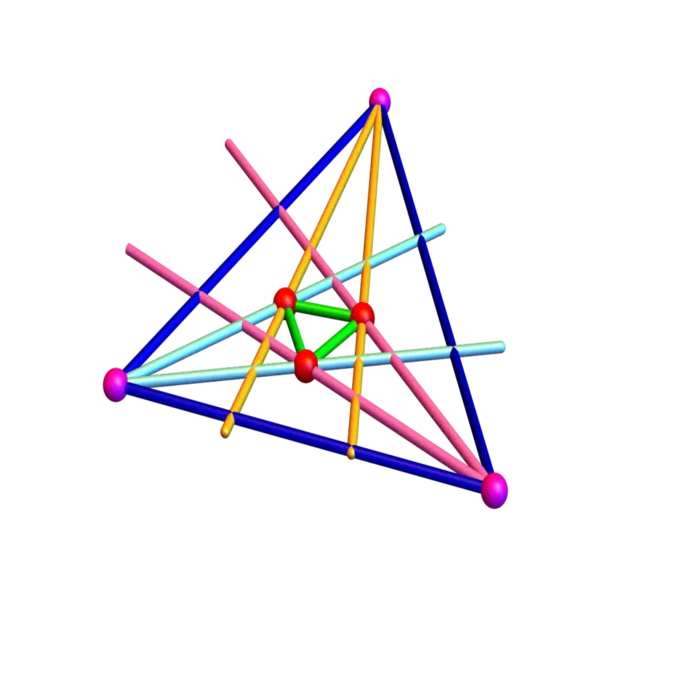
9.2.12 The Challenge of Morley’s Theorem
Lets look at the Morley theorem in planar geometry. It tells that in any triangle, the angle trisector intersections are an equilateral triangle. Can you find a proof? Don’t try. Without looking it up, finding an intuitive proof is very, very hard.
9.2.13 Continuity of \(x\sin(1/x)\): A Closer Look
Finally we come back to the question early on whether the function \[f(x)=x \sin (1 / x)\] is continuous. The answer is yes. The function \(g(x)=\sin (1 / x)\) is not continuous as we can find arbitrary small \(x=1 /(\pi / 2+2k \pi)\) for which the function is \(g(x)=1\) and arbitrary small \(x=1 /(2k \pi-\pi / 2)\) for which the function is \(g(x)=-1\). For the function \(f(x)\) however we can say that \(|f(x)| \leq|x|\). So, if \(x\) is small, also \(|f(x)|\) is small. If you want to check your intuition with formal statements: given any \(\epsilon>0\) we can find a \(\delta>0\) (namely \(\delta=\epsilon\)) such that if \(|x| \leq \delta\) then \(|f(x)| \leq \epsilon\).
EXERCISES
Exercise 1. Prove that there was a time in your life when the length of your largest tooth in millimeters was your height in meters.
Exercise 2. Is the function \(f(x, y)=(x^{4}+y^{4}) /(x^{2}+y^{2})\) continuous everywhere if we assume \(f(0,0)=0\)? Intuition is a bit harder here as we divide \(0\) over \(0\) at the origin and are in two variables. In either case, give a reason for your answer. You can already use polar coordinates \(x=r \cos (\theta)\), \(y=r \sin (\theta)\). Coordinates will be talked about more next week.
Exercise 3. Use the intermediate value theorem to derive Rolle’s theorem using an "intuitive" argument: if \(f\) is continuously differentiable (meaning \(f^{\prime}(x)\) is continuous) and \(f(0)=f(1)=0\), then there exists a point in \((0,1)\) with \(f^{\prime}(x)=0\).
Exercise 4. A cylinder \(S\) of radius \(1\) and height \(1\) is approximated by a polyhedron with triangles of size \(\epsilon\). If \(S_{n}\) is the polygonal approximation. Does the surface area \(\left|S_{n}\right|\) of the polyhedron and the surface area of the surface \(S\) satisfies \(\left|S_{n}\right| \rightarrow|S|\)? Give an example where the answer is yes.
Exercise 5. As a continuation of 9.4, there is a Chinese lantern type construction which shows that \(\left|S_{n}\right| \rightarrow|S|\) is wrong in general. Look the construction of the Schwarz lantern from 1880 up and describe it.