Gauss' Theorem

 

34.1 INTRODUCTION

34.1.1 Divergence, Flux, and Volume

The fastest way to compute the volume of a complicated solid is to use Gauss theorem. It turns out that the flux of the vector field \(F=[x, 0, 0]\) through the boundary surface \(S\) of a solid \(E\) is the volume. Gauss theorem equates this flux with the creation of the field inside. If you draw out the vector field \(F=[x, 0, 0]\) you see that it expands things out. Look at the unit cube. The field does not flow through the \(y=0\), \(y=1\) or \(z=0\) and \(z=1\) faces because the field is parallel there. On \(x=0\), the field is zero. The only face of the cuboid where some field passes is \(x=1\) and the field is leaving there. So, something must be created inside. This creation of field is called divergence. If \(F=[P, Q, R]\), then \(\operatorname{div}(F)=P_{x}+Q_{y}+R_{z}\). In the case \(F=[x, 0, 0]\) we have constant divergence \(1\). We have seen that \[\iint_{E} \operatorname{div}(F) \,d V=\iint_{S} F \cdot d S.\] You can also see that for fields like \(F=[0, x, 0]\) the total flux is zero as what comes in on one side goes out on the other side. Any linear linear field \(F\) as a linear combination of fields in the class \[\begin{aligned} &[x, 0,0], \quad [y, 0,0], \quad [z, 0,0],\\ &[0, x, 0], \quad [0, y, 0], \quad [0, z, 0],\\ &[0,0, x], \quad [0,0, y], \quad [0,0, z] \end{aligned}\] for which the divergence theorem is satisfied.

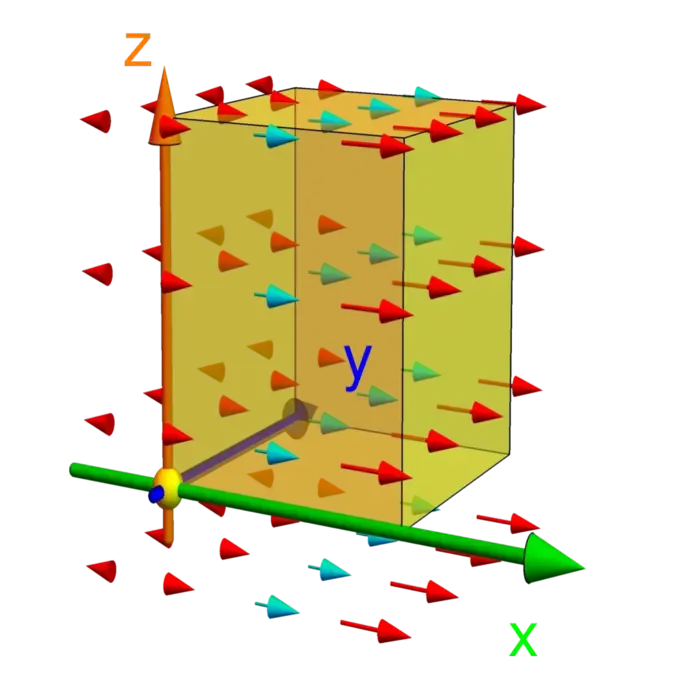
Figure 1. The vector field \(F=[x, 0,0]\) has constant divergence \(1\). The flux through \(\iint_{S} F \,d S\) through the boundary is \(\iiint_{E} \operatorname{div}(F) \,d V\).

34.1.2 Gauss’s Law, Laplacian, and Newton’s Law

Gauss law \(\operatorname{div}(F)=f=4 \pi G \rho\) describes the gravitational field induced from a mass density \(\rho\) and gravitational constant \(G\). The picture is that mass is a source for the field. We will see that with the help of the divergence theorem, this equation implies Newton’s law of gravity \(F=M G / r^{2}\) induced by a mass \(M\). Since the gravitational field does not to allow perpetual motion, it is a gradient field and \(F=\nabla V\). The combination \(\Delta=\operatorname{div}\) (grad is called the Laplacian Gauss law now produces the Poisson equation \(\Delta V=f\) which determines potential \(V=\Delta^{-1} f\) from the mass density. The inverse of \(\Delta\) also called Green function. Once we have such a description, we have now gravity on any space with a Laplacian. We can study gravity on a surface like the sphere or in \(\mathbb{R}^{n}\), where the force is proportional to \(1 / r^{n-1}\). We will see in the proof part how we can so define gravity on any finite network.

34.2 LECTURE

34.2.1 Divergence and Gauss’s Theorem: Connecting Integrals

The divergence of a vector field \(F=[P, Q, R]\) in \(\mathbb{R}^{3}\) is defined as \[\operatorname{div}(F)=\nabla \cdot F=P_{x}+Q_{y}+R_{z}.\] Let \(G\) be a solid in \(\mathbb{R}^{3}\) bound by a surface \(S\) made of finitely many smooth surfaces, oriented so the normal vector to \(S\) points outwards. The divergence theorem or Gauss theorem is

Theorem 1. \(\iiint_{G} \operatorname{div}(F) \,d V=\iint_{S} F \cdot d S\).

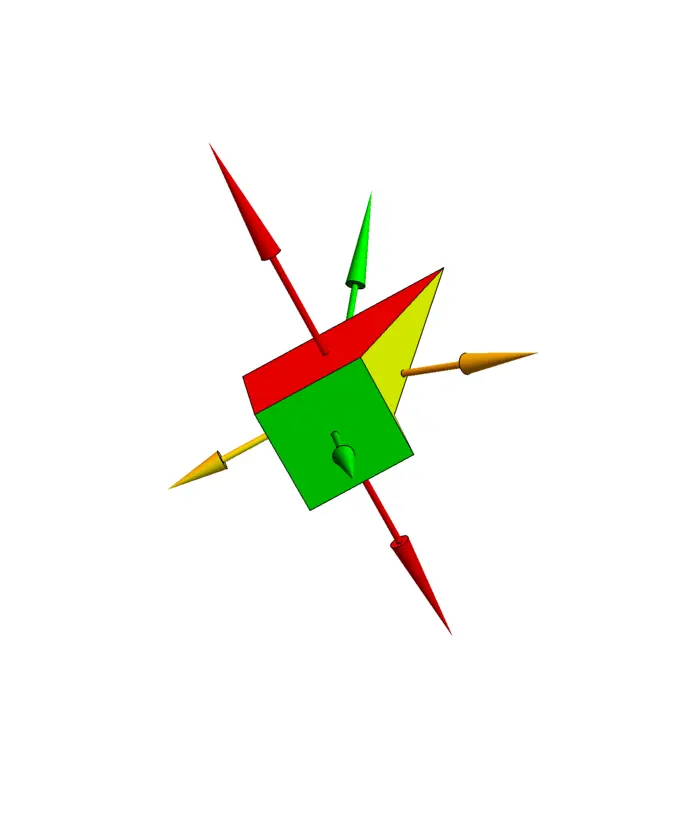
Figure 2. The boundary of a solid is oriented outwards. The divergence measures the expansion of a box flowing in the field. The flux of \(\operatorname{curl}(F)\) through a closed surface is \(0\). No field is created inside.

Proof. If \(G\) is a solid of the form \[G=\{(x, y, z) \mid(x, y) \in U,\ g(x, y) \leq z \leq h(x, y)\} \quad \text{and} \quad F=[0,0, R],\] then \[\iiint_{G} \operatorname{div}(F) \,d V=\iint_{U} \int_{g(x, y)}^{h(x, y)} R_{z} \,d z \,d y \,d x\] which is \[\iint_{G} \Big(R(x, y, h(x, y))-R(x, y, g(x, y))\Big) d y \,d x.\] The flux of \(F=[0,0, R]\) through a surface \(r(u, v)=[u, v, h(u, v)]\) is \[\iint_{G} \big[0,0, R(u, v, h(u, v))\big] \cdot[-g_{u}, g_{v}, 1] \,d v \,d u=\iint_{G} R(x, y, h(x, y)) \,d x \,d y\] Similarly, the flux through the bottom surface is \(-\iint_{G} R(x, y, g(x, y)) \,d x \,d y\). In general, write \[F=[P, Q, R]=[P, 0,0]+[0, Q, 0]+[0,0, R]\] to get the claim for solid which are simultaneously bound by graphs of functions in \(x\) and \(y\), or \(y\) and \(z\) or \(x\) and \(z\). A general solid can be cut into such solids. ◻

34.2.2 Inward or Outward? Divergence as the Measure of Field Flow

The theorem gives meaning to the term divergence. The total divergence over a small region is equal to the flux of the field through the boundary. If this is positive, then more field leaves than enters and field is "generated" inside. The divergence measures the expansion of the field. The field \(F(x, y, z)=[x, 0,0]\) for example expands, while \(f(x, y, z)=[-x, 0,0]\) compresses. \(F(x, y, z)=[y, z, x]\) is "incompressible".

34.2.3 Generalizing Gauss’s Law: Divergence in m Dimensions

The divergence theorem holds in any dimension \(m\). If \(F=[F_{1}, \cdots, F_{m}]\) is the vector field, then \(\partial_{x_{1}} F_{1}+ \cdots +\partial_{x_{m}} F_{m}\) is defined as the divergence of \(F\). If \(G\) is an \(m\)-dimensional region with boundary \(S=s(G)\), then the flux of \(F\) through \(S\) is defined as \[\int_{G} F(s(u)) \cdot n(s(u))\,|d s(u)|,\] where \(n(s(u))\) is a unit normal vector. This can be explained a bit better using the language of differential forms which is introduced next time.

34.2.4 Divergence, Curl, and Green’s Theorem: A Two-Dimensional Twist

The divergence of \(F=[P, Q]\) is defined as \(P_{x}+Q_{y}\). If \(F^{\perp}=[Q,-P]\) is the turned vector field, then \(\operatorname{div}(F^{\perp})=Q_{x}-P_{y}\) is the curl of \(F\). Green’s theorem tells that \(\iint_{G} \operatorname{curl}(F) \,d x \,d y\) which is \(\iint_{G} \operatorname{div}(F^{\perp}) \,d x \,d y\) is the line integral \(\int_{C} F \cdot d r\). The line integral for \(F\) is the flux integral for \(F^{\perp}\). The two dimensional divergence theorem is Green’s theorem "turned".

34.3 EXAMPLES

Example 1. Problem: Compute the flux of \(F=[x, y, z]\) through the sphere of radius \(\rho\) bounding a ball \(G\), oriented outwards.
Solution: As \(\operatorname{div}(F)=3\) we have \[\iiint_{G} \operatorname{div}(F) \,d V=3 \operatorname{Vol}(G)=3 \cdot 4 \pi \rho^{3} / 3.\] The flux through the boundary is \(\iint_{S} F \cdot d S\). As in spherical coordinates, \[F(r(\phi, \theta)) \cdot r_{\phi} \times r_{\theta}=\rho^{3} \sin (\phi),\] the flux is \[\int_{0}^{2 \pi} \int_{0}^{\pi} \rho^{3} \sin (\phi) \,d \phi \,d \theta=4 \pi \rho^{3}\] also.

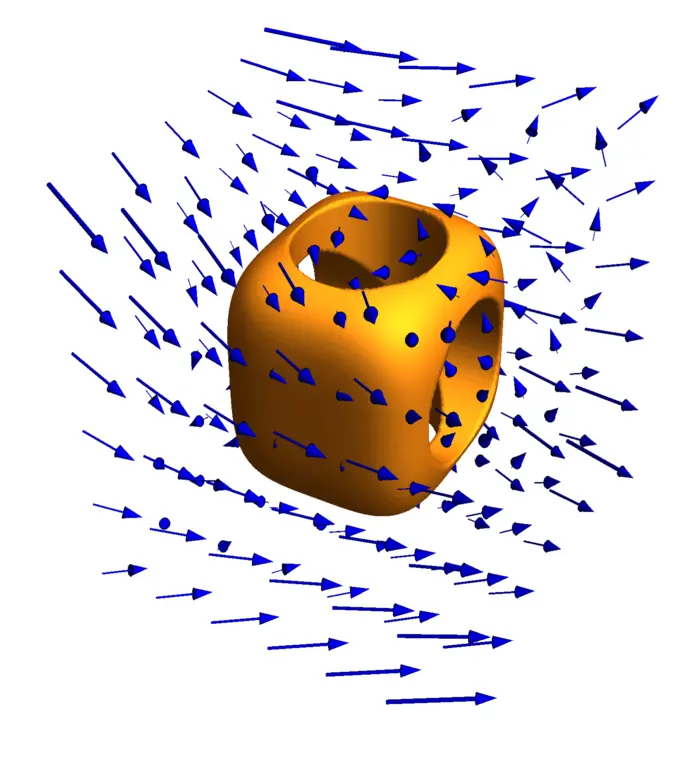
Example 2. Problem: What is the flux of the vector field \[F(x, y, z)=\big[6 x+y^{3}, 3 z^{2}+8 y, 22 z+\sin (x)\big]\] through the solid \[G=[0,3] \times[0,3] \times[0,3] \setminus \big([0,3] \times[1,2] \times[1,2] \cup [1,2] \times[0,3] \times[1,2] \cup [0,3] \times[0,3] \times[1,2]\big)\] which is a cube with three perpendicular cubic holes which is the first stage of the Menger sponge construction?
Solution: As \(\operatorname{div}(F)=22+8+6=36\), the result is \(36\) times the volume of the solid which is \(36(27-7)=720\).

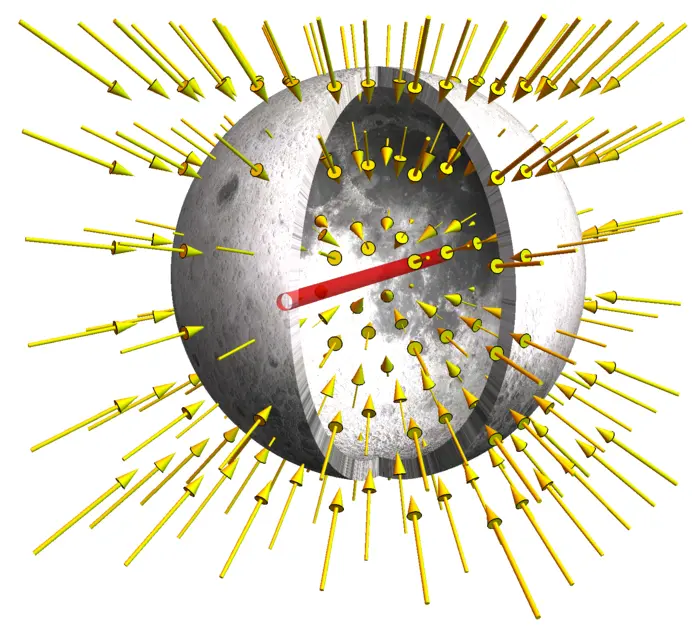
Figure 3. The gravity inside the moon is such that an elevator crossing the moon oscillates like a harmonic oscillator. The flux of \(F=[0,0, z]\) through a surface is the volume inside.

Example 3. Problem: How does the gravitational field look like inside the moon in distance \(\rho\) to the origin?
Solution: A direct computation of summing up all the field values \[F(x)=\iint_{G}(x-y) /|x-y|^{3} \,d y\] is difficult as we can not compute in spherical coordinates. Fortunately we have the divergence theorem. The field \(F(x)\) has constant length \(F(\rho)=|F(x)|\) for \(x\) on a sphere \(S(\rho)\) of radius \(\rho\) and points inwards. So \[\iint_{S(\rho)} F \cdot d S=-4 \pi \rho^{2} F(\rho).\] Gauss was able to write down the gravitational field as a partial differential equation , where \(\sigma(x)\) is the mass density of the solid. We see then with the divergence theorem that \(\iiint_{B(\rho)} 4 \pi \sigma(x) \,d x\) is equal to \(-4 \pi \rho^{2} F(\rho)\). Assuming \(\sigma\) to be constant, we have \[4 \pi(4 \pi \rho^{3} / 3) \sigma=-4 \pi \rho^{2} F(\rho)\] which gives \(F(\rho)=(4 \sigma / 3) \rho\). The field grows linearly inside the body. If \(\rho\) is bigger than the radius of the moon, then \(\iiint_{B(\rho)} 4 \pi \sigma(x) \,d x\) is \(4 \pi M\), where \(M=\iiint_{G} \sigma(x) \,d x\) is the mass of the moon. We see that in that case \(F(\rho)=M / \rho^{2}\), which is the Newton law.

Example 4. Problem: Compute using the divergence theorem the flux of the vector field \[F(x, y, z)=[2342434 y, 2 x y, 4 y z]^{T}\] through the unit cube \([0,1] \times[0,1] \times[0,1]\) which is opened on the top.
Solution: the divergence of \(F\) is \(2 x+4 y\). Integrating this over the unit cube gives \(1+2=3\). The flux through all \(6\) faces is \(3\). The flux through the face \(z=1\) is \[\int_{0}^{1} \int_{0}^{1} 4 y \,d x \,d y=2.\] We have to subtract this and get \(3-2=1\).

Example 5. Similarly as Green’s theorem allowed area computation using line integrals the volume of a region can be computed as a flux integral: take a vector field \(F\) with constant divergence \(1\) like \(F(x, y, z)=[0,0, z]\). We have \[\iint_{S}[0,0, z] \cdot d S=\operatorname{Vol}(G).\] For example, For an ellipsoid \(x^{2} / a^{2}+y^{2} / b^{2}+z^{2} / c^{2}\), where the parametrization is \[r(\phi, \theta)=[a \sin (\phi) \cos (\theta), b \sin (\phi) \sin (\theta), c \cos (\phi)],\] we have \[[0,0, c \cos (\phi)][a b \sin (\phi) \cos (\phi)]=a b c \sin (\phi) \cos ^{2}(\phi)\] leading to \(2 \pi a b c \times 2 / 3=4 \pi a b c / 3\).

Example 6. A computer can determine the volume of a solid enclosed by a triangulated surface by computing the flux of the vector field \(F=[0,0, z]\) through the surface. The vector field has divergence \(1\) so that by the divergence theorem, the flux gives the volume. A computer stores a geometric object using triangles. Assume \(A B C\) is that triangle. If \(n=A B \times A C\) points outside the region, then the flux is \(F \cdot n / 2\). A computer can now add up all these values and get the volume.

Figure 4. A cow, a Klein bottle and a car from the Mathematica example files and produce closed surfaces. The Klein bottle does not have an interior however.

EXERCISES

Exercise 1. Use the divergence theorem to calculate the flux of \(F(x, y, z)=[x^{3}, y^{3}, z^{3}]^{T}\) through the sphere \(S: x^{2}+y^{2}+z^{2}=1\), where the sphere is oriented so that the normal vector points outwards.

Exercise 2. Assume the vector field \[F(x, y, z)=\left[5 x^{3}+12 x y^{2}, y^{3}+e^{y} \sin (z), 5 z^{3}+e^{y} \cos (z)\right]^{T}\] is the magnetic field of the sun whose surface is a sphere of radius \(3\) oriented with the outward orientation. Compute the magnetic flux \(\iint_{S} F \cdot d S\).

Exercise 3. Find the flux of the vector field \(F(x, y, z)=[x y, y z, z x]^{T}\) through the solid cylinder \(x^{2}+y^{2} \leq 1\), \(0 \leq z \leq 2\).

Exercise 4. Find the flux of \[F(x, y, z)=[x+y+z, x+z, z+y]^{T}\] through the Menger sponge \(M_{n}\) defined in the unit cube and take the limit \(n \rightarrow \infty\).

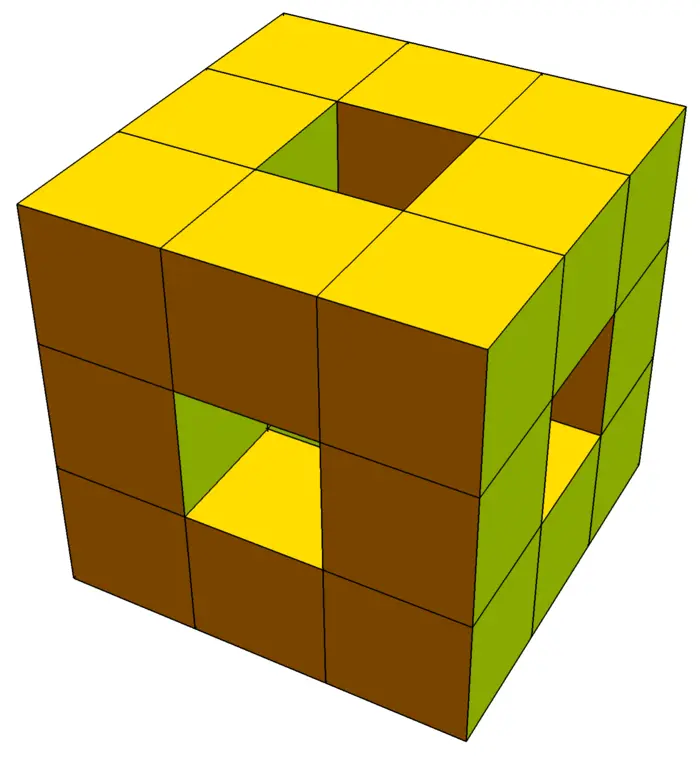
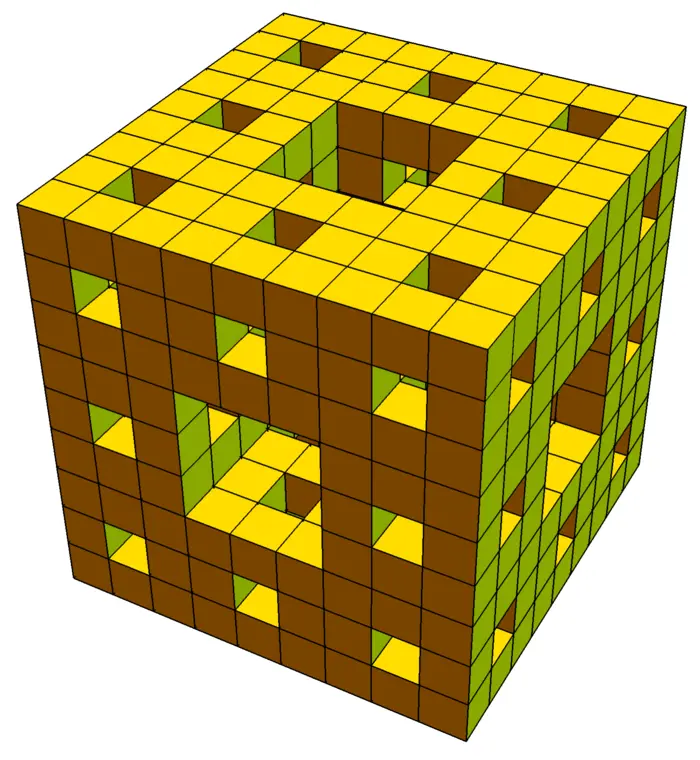
Figure 5. Approximations to the Menger sponge.

Exercise 5. Compute the flux of the vector field \[F(x, y, z, w)=\big[x+2 y^{2}, 3 x+4 z^{5}, 6 z+8 w^{9}, 7 w+9 x^{10}\big]^{T}\] through the three \(3\)-sphere \(x^{2}+y^{2}+z^{2}+w^{2}=1\) in \(\mathbb{R}^{4}\), oriented outwards.