Discrete Vector Calculus

 

33.1 INTRODUCTION

33.1.1 Discrete Calculus

In this seminar as well as the one next week, we redo calculus on finite networks. This is how multi-variable calculus of the future might look like. There is no infinity, there are no limits. The mathematics is the same. We will formulate first the fundamental theorem of line integral, Green and Stokes theorem \(\int_{G} \,d F=\int_{d G} F\) on such a world.

Figure 1. Two networks. The first one is a two dimensional surface, the second a three dimensional solid.

33.1.2 Network Calculus

A finite network is a graph \((V, E)\), where \(V\) is a finite set of nodes called vertices and where \(E\) are connections between nodes. There are no loops in that connections connect different nodes and also, there is only one connection possible between two points. One calls \((V, E)\) a finite simple graph. Now similarly as we introduce coordinate systems in our space telling what is north, south, up or down, etc, we assign when doing computations an orientation on the edges. This is pretty arbitrary but usually done any way when we implement a graph on a computer. For example \[(G, V)=\big(\{1,2,3,4\},\{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\}\big)\] is a graph with \(4\) nodes, where all nodes are connected to each other. When doing calculus, we look at functions on nodes, functions on edges, functions on triangular sugraphs as well as functions on tetrahedral subgraphs.

33.2 SEMINAR

33.2.1 Network Fields and Gradients

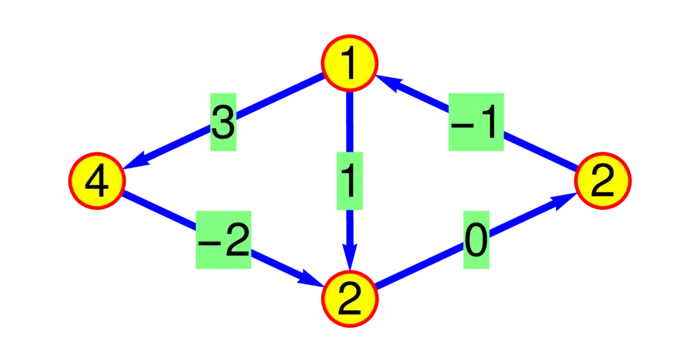
In this seminar, we replace the space \(\mathbb{R}^{n}\) with a finite graph \(G=(V, E)\), where \(V\) is a set of vertices called nodes and \(E\) is a set of edges called connections. A scalar field is a function \(f\) which assigns to every vertex \(x\) a function value \(f(x)\). We assume the vertices to be ordered leading to an order of the edges: draw an arrow \(a \rightarrow b\) if \(a. This a priori order has no effect on any of the theorems. A vector field assigns to every edge a number \(F(x)\). A curve is a list of nodes \(x_{1}, x_{2}, \ldots, x_{n}\) such that \(x_{1}\) is connected to \(x_{2}\), \(x_{2}\) is connected to \(x_{3}\), etc. The gradient \(\nabla f\) of a scalar function \(f\) is the vector field \(F(a, b)=f(b)-f(a)\). The line integral \(\int_{C} F \cdot d r\) is defined as \(\sum_{e \in C} F(e) \,d e\). We just add up the function values of \(F\) along the curve \(C\), positive \(d e=1\) if we go with the arrow, negative \(d e=-1\) if we go against the arrow.

Problem A: Check the closed loop property of the gradient field \(\nabla f\) shown in the graph of Figure (33.2).

Figure 2. We see a graph with \(4\) vertices and \(5\) edges. The scalar function \(f\) is given by the values on the round vertices. It defines a gradient vector field \(F=\nabla f\) which is a function on edges.

33.2.2 Discrete Line Integral Theorem

The discrete fundamental theorem of line integrals is:

Theorem 1. If \(F=\nabla f\) is a gradient field and \(C\) is a curve from \(a\) to \(b\), then \(\int_{C} \nabla f \cdot d r=f(b)-f(a)\).

Problem B: Prove the discrete fundamental theorem of line integrals by induction on the length of the curve \(C\).

33.2.3 Unit Spheres

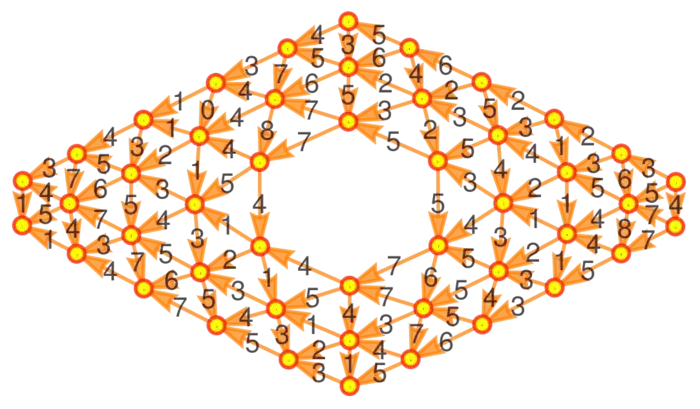
Let’s look at some terminology. Given a vertex \(x\) in a graph \(G\), the unit sphere \(S(x)\) of \(x\) is the sub-graph generated by the set of vertices directly attached to \(x\). The unit sphere of the vertex labeled \(11\) in Figure (33.3) for example is the circular graph generated by the vertices \(\{2,4,9,8,7,9\}\). It is a "circle". The unit sphere of the vertex with label \(4\) in that figure is the graph generated by the vertices \(\{11,7,1\}\). It is an linear graph, a half circle.

33.2.4 Discrete Regions

A graph is called a discrete two-dimensional region, if every unit sphere \(S(x)\) is a circular graph with \(4\) or more vertices or a linear graph with \(2\) or more vertices. The set of vertices for which the unit sphere is circular form the interior of the region. The other vertices form the boundary of the region. A two dimensional region without boundary is called closed. In Figure (33.3) for example, there are \(4\) interior points and \(9\) boundary points. In Figure (33.5), we see a closed region.

33.2.5 Discrete Curl

The curl of a vector field \(F\) is a function on the triangles \(T\) of \(G\). To get the value of the triangle \((a, b, c)\) we form the line integral of \(F\) along the curve \[C: a \rightarrow b \rightarrow c \rightarrow a.\] Each triangle is assumed to be oriented (if drawn in the plane, then counter clockwise).

33.2.6 Discrete Flux

Given a function \(F\) on the triangles of a region \(G\) which is oriented, the flux integral \(\iint_{G} F(x) \,d A\) is defined as \(\sum_{t \in T} f(t)\), where \(T\) is the set of triangles in \(G\).

Figure 3. A gradient field on a two-dimensional region with boundary. Check that the curl is zero everywhere.

33.2.7 Discrete Green’s Theorem

Here is the discrete Green’s theorem:

Theorem 2. If \(F\) is a vector field on a \(2\)-dimensional discrete region \(G\), and the boundary \(C\) is oriented in a compatible way with the region, then \[\iint_{G} \operatorname{curl}(F) \,d A=\int_{C} F \cdot d r.\]

33.2.8 Applying Green’s Theorem: Curl, Flux, and Verification

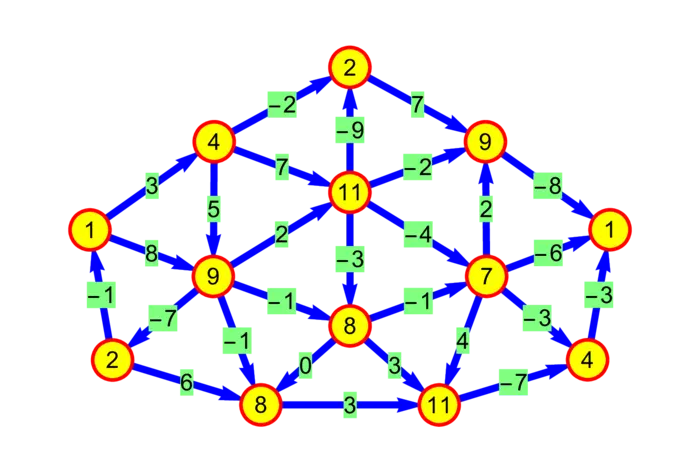
Figure (33.4) shows a region equipped with a vector field \(F\).

Problem C: Write in the curl of the vector field in Figure (33.4).

Figure 4. A vector field on a two-dimensional discrete region.

Problem D: Prove the discrete Green theorem by induction on the number of triangles.

EXERCISES

Exercise 1. Check that the curl of a gradient field is zero: \(\operatorname{curl}(\operatorname{grad}(f))=0\) for a general triangle: draw an oriented triangle. Define \(F=\nabla f\) for a scalar function \(f\), \(1\) then compute \(\operatorname{curl}(F)\).

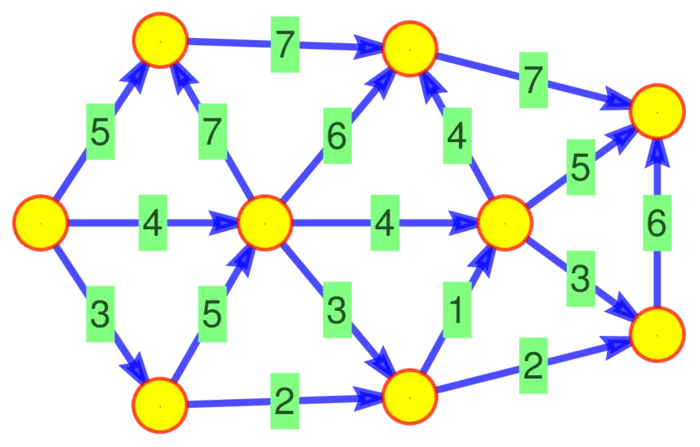
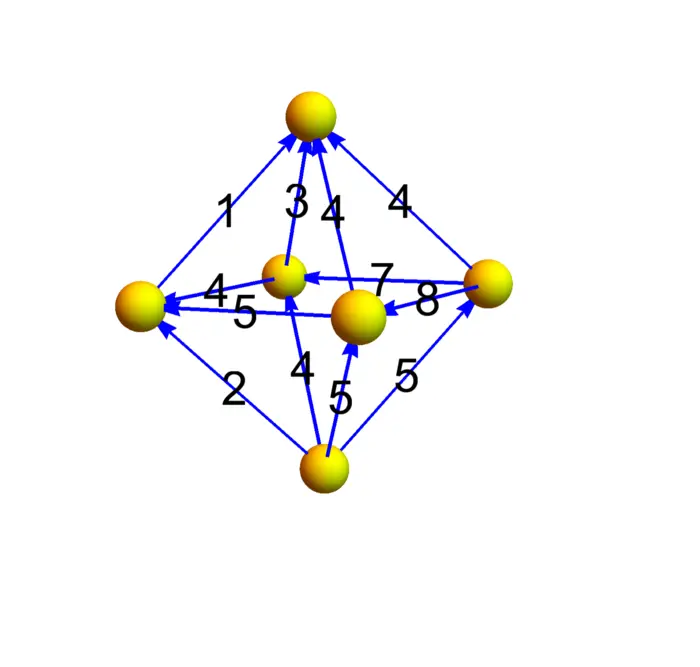
Exercise 2. Figure (33.5) shows a vector field on the octahedron a two dimensional discrete sphere. Determine all the curls and check that the sum of all curls is zero. You have checked \(\int_{S} \operatorname{curl}(F) \,d S=0\) for a closed surface.

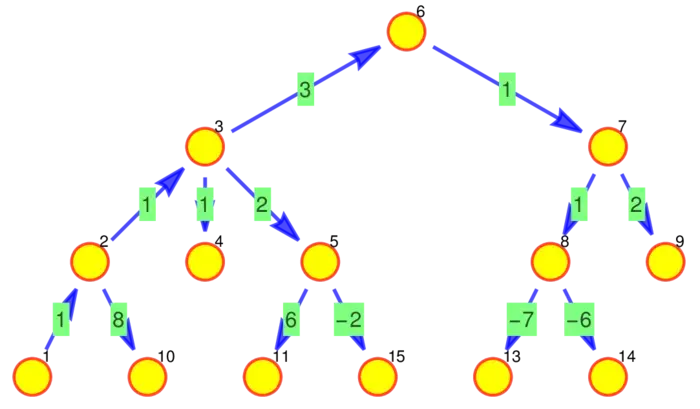
Figure 5. On a closed discrete \(2\)-dimensional region like an octahedron, the sum of the curls of a vector field are zero.

Exercise 3. Figure (33.6) shows a tree, a graph without closed loops. Find a potential function \(f\). You can assume that the value at the top node is \(0\). You see then that the function value right below is \(1\). Get all the function values of the potential.

Exercise 4. Find a vector field on a circular graph with \(5\) vertices which is not a gradient field.

Figure 6. On a tree, every vector field is a gradient field.
Figure 7. Fill in a vector field which is not a gradient field.

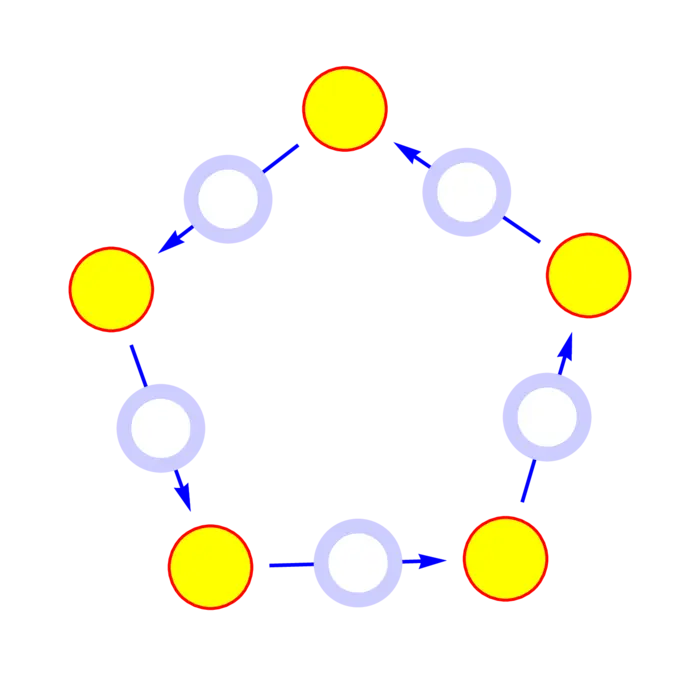
Exercise 5. Check Green’s theorem in the following annular region. Compute both the line integral \(\int_{C} F \,d r\) along the boundary (which has two components) as well as \(\iint_{G} \operatorname{curl}(F) \,d A\), the sum of the curvatures over all triangles.

Figure 8. The region for Exercise 33.5.