Cross Product

4.1 INTRODUCTION

4.1.1 Vector Multiplication Evolution

We have seen that we can multiply square matrices and get again a matrix. Wouldn’t it be nice if we could also multiply two vectors and get a vector back. The dot product, which is the matrix product of a row vector with a column vector gave us a number. The matrix product of a column vector with a row vector would give us a square matrix. How can we design a product of column vectors which again gives us a column vector? This was the question which William Rowan Hamilton pondered for many years. The story goes that every morning, when he would come down to the breakfast table, his young son would ask "Dad, can you already multiply triplets?" to which William answered: "No Son, I do not know how to do that yet".

4.1.2 Quaternions and Cross Product

Eventually, Hamilton succeeded. The legend goes that while walking with his wife along the Royal Canal in Dublin, while crossing the Brougham bridge, he suddenly got the inspiration: one has to multiply quadruplets! These numbers would be written as \(a+b i+c j+d k\) where \(i, j, k\) are symbols satisfying \(i^{2}=j^{2}=k^{2}=i j k=-1\). He was so happy that he would would devote the rest of his life with these numbers. Now it turns out that this algebra also produces a product of vectors which is called the cross product. It has a lot of nice properties like that the product of two vectors is perpendicular and that the length is related to area. It also has amazing applications in physics.

4.2 LECTURE

4.2.1 Uniqueness of \(\mathbb{R}^{3}\)

The three dimensional space \(\mathbb{R}^{3}\) is special. It is not only the only Euclidean space in which the Kepler problem is stable¹, it also features a cross product \(v \times w\) which is in the same space. Such a product can be defined in \(\mathbb{R}^{n}\) but it produces a vector in \(\mathbb{R}^{n(n-1) / 2}\). It happens that for \(n=3\) that the result is again in \(\mathbb{R}^{3}\). The problem of "multiplying triplets" has been pondered by William Hamilton in the first half of the 19th century and is related to the fascinating story of quaternions. The discovery of quaternions was simultaneously the birth place of the dot and cross product.

4.2.2 Cross Product Properties

The cross product of two vectors \(v=\left[v_{1}, v_{2}, v_{3}\right]^{T}\) and \(w=\left[w_{1}, w_{2}, w_{3}\right]^{T}\) is

\[\left[\begin{array}{l} v_{1} \\ v_{2} \\ v_{3} \end{array}\right] \times\left[\begin{array}{l} w_{1} \\ w_{2} \\ w_{3} \end{array}\right]=\left[\begin{array}{l} v_{2} w_{3}-v_{3} w_{2} \\ v_{3} w_{1}-v_{1} w_{3} \\ v_{1} w_{2}-v_{2} w_{1} \end{array}\right]\]

Take the dot product with \(v\) or \(w\) to see that \(v \times w\) is perpendicular to both \(v\) and \(w\). Obvious is also \(v \times w=-w \times v\). The product is handy for constructions in \(\mathbb{R}^{3}\). The vectors \(v, w, v \times w\) are oriented like the first three fingers on the right hand: if \(v\) is the thumb, \(w\) is the pointing finger, then \(v \times w\) is the middle finger. Let \(v \cdot w=|v||w| \cos (\alpha)\):

4.2.3 Geometric Sine Applications

Given a triangle with side lengths \(a, b, c\) and angles \(\alpha, \beta, \gamma\), where \(\alpha\) is opposite to \(a\) etc. We have the following \(\boldsymbol{\sin}\)-formula

4.2.4 Geometric Area Insights

This is useful in applications as to define the area of the parallelogram as \(|v \times w|\). That this is justified can be seen in two dimensions and:

4.2.5 Triple Scalar Product

The scalar \(u \cdot(v \times w)\) is called the triple scalar product of \(u, v, w\). Its sign defines an orientation of the three vectors. It is also the determinant of the matrix \[\left[\begin{array}{lll} u_{1} & v_{1} & w_{1} \\ u_{2} & v_{2} & w_{2} \\ u_{3} & v_{3} & w_{3} \end{array}\right].\] The absolute value of \(u \cdot v \times w\) defines the volume of the parallelepiped spanned by \(u\), \(v\) and \(w\). Without the absolute value, we also speak of signed volume.

4.2.6 Side Remark: Cross Product in Higher Dimensions

In higher dimensions, the cross product is called exterior product. One uses \(\wedge\) rather than \(\times\) which is used in three dimensions. If \(I=(i, j)\) is a choice of two elements in \(\{1,2, \ldots, n\}\) and \(v, w\) are two vectors in \(\mathbb{R}^{n}\), then \((v \wedge w)_{I}=\) \(v_{i} w_{j}-v_{j} w_{i}\). The formula \(|v \wedge w|=|v||w| \sin (\alpha)\) still holds and the proof is the same. We only need again to verify the Cauchy-Binet formula \(|v|^{2}|w|^{2}-(v \cdot w)^{2}=|v \wedge w|^{2}\). But this is better done using matrices. If \(A\) is the matrix which contains \(v, w\) as columns, then \(\operatorname{det}(A^{T} A)=\sum_{P} \operatorname{det}(A_{P})^{2}\), where the sum on the right is over all \(2 \times 2\) submatrices \(A_{P}\) of \(A\). The expression \(\operatorname{det}(A_{P})\) is called a minor. Cauchy-Binet formula is super cool². By the way, if we have \(k\) vectors and build \(A \in M(n, k)\), a matrix which has these vectors as columns. Now, \(\operatorname{det}(A^{T} A)\) is the volume of the parallelepiped spanned by these vectors. And Cauchy-Binet writes this as a sum of squares of \(k\)-dimensional volumes of projections which is in some sense a generalization of Pythagoras.

4.3 EXAMPLES

4.4 ILLUSTRATIONS

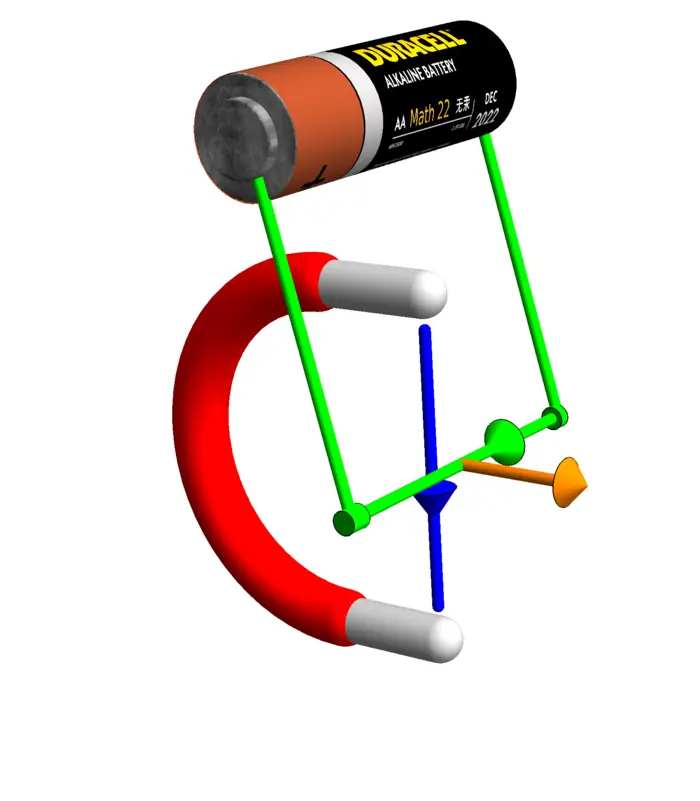
EXERCISES