Creativity
Table of Contents
- 12.1 INTRODUCTION
- 12.2 SEMINAR
- 12.2.1 Master Midterms with Mind Maps
- 12.2.2 Knowledge: The Spark of Creativity
- 12.2.3 Tricky Sticks
- 12.2.4 Unlocking Hidden Creativity: Lessons from Fritz Zwicky
- 12.2.5 Dark Matter and Dirty Jokes: The Story of Fritz Zwicky
- 12.2.6 The Morphological Box Technique
- 12.2.7 Zwicky’s Wild Space Ideas
- 12.2.8 Rethinking Zwicky’s Solar Travel Idea
- 12.2.9 From Bathroom Tiles to Cherry Puzzles
- EXERCISES
12.1 INTRODUCTION
12.1.1 How Mathematicians Find Proofs?
You have seen a couple of proofs so far. You might wonder, how was the proof found? For example, we have seen the Cauchy-Schwarz inequality \(|v \cdot w| \leq|v||w|\). How did one get to the idea to first assume \(|w|=1\) then define \(a=v \cdot w\) and look at \[0 \leq(v-a w) \cdot(v-a w)=|v|^{2}-a^{2}?\] In this case the crucial input comes from a visual picture as we can see \(v-a w\) as a vector perpendicular to the vector \(w\). If you are given the problem to prove the Cauchy-Schwarz inequality without looking up the proof, this is a very difficult task. It is difficult because it needs an idea. Getting ideas is what creativity is about.

12.2 SEMINAR
12.2.1 Master Midterms with Mind Maps
In a bit more than a week we have to start thinking about our first midterm, let us organize the knowledge accumulated so far. We can do that in various ways. One technique is a mind map. It allows on one picture to organize a vast amount of content and see connections which might otherwise be missed. In Figure (12.2) we started to build such a mind map. There are lots of branches still missing, even main ones. One could start also with one entry like "matrix", put it in the center then build connections to other objects definitions or results.
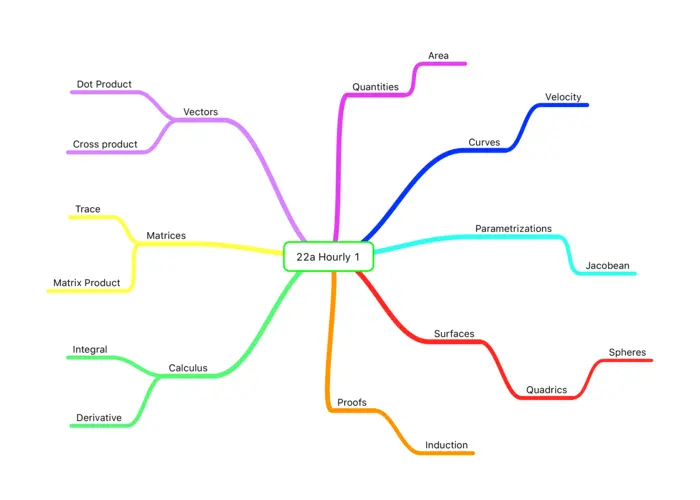
12.2.2 Knowledge: The Spark of Creativity
What does this have to do with creativity? It turns out that in order to be creative, one has to have a fertile base of knowledge. You can not assemble new building blocks before possessing and understanding some already. In order to prove the point that knowledge is important, one can also look at computer science and especially the field artificial intelligence (AI). One of the great pioneers in AI, Marvin Minsky once wrote: "the best way to solve a problem is to know how to solve it". The modern paradigms in machine learning confirm that in order to train an AI entity, one has to feed in a lot of knowledge to work with. New models come then through data fitting, gradient decent methods or more sophisticated algorithms.1
Problem A: Make a mind map of the most important facts which have appeared in the course so far. Do it on paper, a blackboard, whiteboard or using software. Figure (12.2) makes a start. Refine it as much as possible.
12.2.3 Tricky Sticks
To illustrate how difficult it can be to get a new solution, try the following problem. Of course, if you know the answer or have seen it already, it can be easy. If you have never seen it, it can be very hard. It is important that you try to find the solution for at least a half an hour even if you should not be successful.
Problem B: Given \(6\) sticks of the same length \(1\), arrange them so that you get \(4\) equilateral triangles of side length \(1\).
12.2.4 Unlocking Hidden Creativity: Lessons from Fritz Zwicky
Finding proofs of theorems needs creativity. Creativity is neither "God-given" nor inherited; it can be be trained like everything else. To back this claim up, we refer to a scientist who has demonstrated creativity by discovering new things which nobody else has thought about before. It is the Swiss scientist Fritz Zwicky who taught at Caltech and wrote a book "Everybody a genius". Why does Zwicky have "street cred"? Well, he was not only extraordinarily creative, he also developed and communicated creativity techniques that work and have been used since both in industry and academia.


12.2.5 Dark Matter and Dirty Jokes: The Story of Fritz Zwicky
First to the credentials: Fritz Zwicky proposed the existence of dark matter, supernovas (together with Walter Baade), neutron stars, galactic cosmic rays, gravitational lensing by galaxies, and galaxy clusters. He was also a pioneer in rocket technology. He proposed and realized the first shot of a human produced object to go into outer space. Each of these achievements alone would merit to be in the list of greatest astronomers of all time. Still, Zwicky is not that well known. Why? Maybe it has to do with the fact that Zwicky used to call his colleagues "spherical bastards". Why spherical? "Because they are bastards from whatever side you looked at them!" No wonder he was not that much admired...
12.2.6 The Morphological Box Technique
One of the techniques is the morphological box. It is very simple. Produce a matrix in which one has one type of objects, ideas or activities on one side and another type of objects, ideas or activities. Now, just go through the matrix and look for connections. Here is such a matrix:
| Earth | Moon | Sun | |
|---|---|---|---|
| shoot | |||
| dig | |||
| travel |
12.2.7 Zwicky’s Wild Space Ideas
Now look what Zwicky proposed: shoot onto the moon (he actually did that with used V2 rockets which had an actual gun on top. At the end of the burn the gun was fired, the bullet would travel to space), he proposed travel by large scale digging through the earth (this is now realized by a company formed by Elon Musk) travel with the sun (the proposal was to travel to a nearby star by moving the entire solar system).
12.2.8 Rethinking Zwicky’s Solar Travel Idea
The matrix entry "dig sun" might come in when realizing Zwicky’s space travel idea. We might have to target part of the sun differently to trigger asymmetric burn and so a travel. By the way there is an entire field of engineering, "macro-engineering". In 1997, I suggested in an essay (to the occasion of the 100th birthday of Zwicky) to implement Zwicky’s idea by deliberate triggering of asymmetric fusion and fission in the Sun. This is mentioned in a macro-engineering book.2
12.2.9 From Bathroom Tiles to Cherry Puzzles
Here is a beautiful problem assigned in a course Math \(101\) taught a couple of years ago taught by Sebastien Vasey. Borrowing a problem from another course does not make much of the point for creativity: but the problem is too beautiful to be missed. It is an example of an induction proof which needs some creativity. Try to solve it.
Problem C: You have bathroom tiles which have three squares arranged in an \(L\) shape. Prove that you can cover a square shaped bath room floor of length and width \(2^{n}\) with such tiles such that one square is left empty.
Problem D: Martin Gardner wrote many books with puzzles. One of them is "The mathematical magic show" (1977). On the book cover of the German edition (1988), there is a famous puzzle: you have a cherry in a glass built by \(4\) matches. Move two of the four matches to get the cherry out of the glass. The glass should have the same shape as before. You are not allowed to move the cherry. Solve the cherry puzzle.

EXERCISES
In all the following question, creativity is key. Your object has to be original. It is ok to modify a known object. And of course, use technology so that one can admire your creation.
Exercise 1. Be creative and generate your own parametrized curve. If you like it enough, you are allowed to name it with your name.
Exercise 2. Be creative and generate your own parametric surface. Again, if the surface is creative enough and the surface is indeed new, you deserve to have the surface named after you.
Exercise 3. Be creative and generate a level surface \(f(x, y, z)=c\). Also here, try to get something which has never been seen.
Exercise 4. Be creative and generate your own coordinate system \(\mathbb{R}^{2}\).
Exercise 5.
- Write a first hourly!
- take it!
- grade it!
Remark: According to the Apocrypha of Krantz (page 79), part a) and b) were once given as an algebraic geometry exam given here at Harvard. It is rumored that this was then used also at the Harvard philosophy department, where (and this is creative too), part c) was added. As far as we know, giving the homework assignment of writing an exam assignment is a first! Heureka! We were creative.