Contradiction and Deformation

 

15.1 INTRODUCTION

15.1.1 Proof by Contradiction

One of the most common fallacies which are done in logical argumentation is to reverse an implication. If \(A\) implies \(B\), then \(B\) implies \(A\). Right? If you are an idiot, you do stupid things. So, if you do stupid things, you are an idiot. This is not true. The implication \(A \Rightarrow B\) does not imply \(B \Rightarrow A\), but it implies \(\neg B \Longrightarrow \neg A\). This is called contradiction. We write \(\neg A\) for the negation of \(A\). Related to contradiction is the method of "Reductio ad absurdum". To prove a statement \(B\) from some statements \(A\), we can assume that \(B\) is false and deduce from this that \(A\) is false.

Figure 1. Reductio ad absurdum. Picture by the Scottish painter John Pettie (1839-1993). This picture is featured on the Wikipedia page about Reductio ad absurdum.

15.1.2 Reversing Implications is a Logical Fallacy: An Example

Here is an example: Let \(A\) be the statement "It rains". And let \(B\) be the statement "The street is wet". Obviously \(A\) implies \(B\). But \(B\) does not imply \(A\). It could be that the street is wet from a rain which stopped earlier or that somebody was cleaning the street. But we can conclude: if the street is not wet, then it does not rain. The statement \(A \Longrightarrow B\) indeed is equivalent to \(\neg B \Longrightarrow \neg A\).

15.1.3 The Beauty and Danger of Proof by Contradiction

Geoffrey Hardy describes as follows: "The proof is by reductio ad absurdum, and reductio ad absurdum, which Euclid loved so much, is one of a mathematician’s finest weapons." But every mathematician who has done proofs knows about the pitfalls. Here is a well formulated statement by Henry Cohn from MIT "Unfortunately, this proof technique can really cause problems for beginners. Typically, what happens is that the proof starts off quite reasonably, and then gets lost in a maze of complexity. Somewhere in the confusion, a mistake is made, which leads to a contradiction. Then it looks like the proof is done, but unfortunately the contradiction has nothing to do with the initial assumption, and comes solely from the mistake in the middle."

15.2 SEMINAR

15.2.1 Beyond Direct Proofs: Contradiction and Deformation Techniques

We have already seen one proof technique, the "method of induction". Other proofs were done either by direct computations or by combining already known theorems or inequalities. Today, we look at two new and fundamentally different proof techniques. The first is the method "by contradiction". The second method is the "method of deformation". Both methods are illustrated by a theorem.

15.2.2 Pythagorean Surprise

The first theorem is one of the earliest results in mathematics. It is the Hypassus theorem from 500 BC. It was a result which shocked the Pythagoreans so much that Hypassus got killed for its discovery. That is at least what the rumors tell.

Theorem 1. The diagonal of a unit square has irrational length.

Proof. \(\fbox{Assume}\) the statement is false and the diagonal has rational length \(p / q\). Then by Pythagoras theorem \(2=p^{2} / q^{2}\) or \(2 q^{2}=p^{2}\). By the fundamental theorem of arithmetic, the left hand side has an odd number of factors 2 , the right hand side an even number. This is a \(\fbox{contradiction}\). The assumption must have been wrong. ◻

Problem A: Prove that the cube root of \(2\) is irrational.

15.2.3 Completing a Geometric Proof of the Irrational Diagonal

Note that the proof relied on the fundamental theorem of arithmetic which assured that every integer has a unique prime factorization.

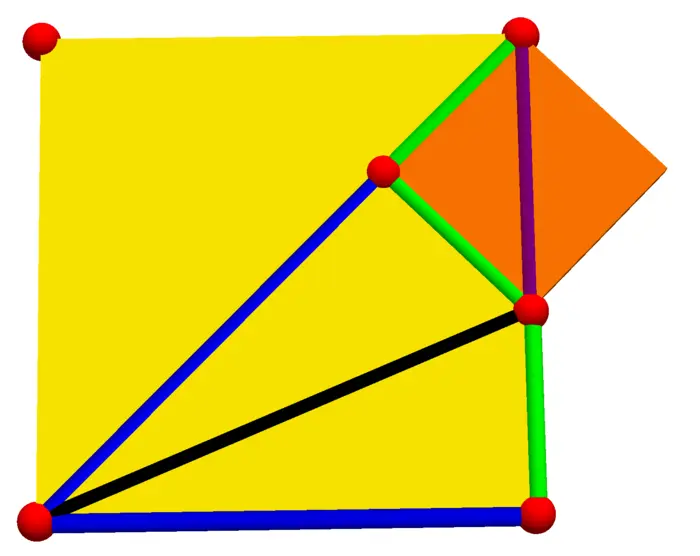
Problem B: Figure (15.2) is a geometric proof by contradiction which does not need the fundamental theorem of arithmetic. Complete the proof.1

Figure 2. \(\sqrt{2}\) is irrational. Start by assuming the side length and diagonal of the large yellow square are integers. Conclude that for the strictly smaller orange square, the side length and diagonal are integers.

15.2.4 Beyond Contradiction

Proofs by contradiction can be dangerous. A flawed proof can "\(\fbox{assume}\) the contrary, mess around with arguments, make a mistake somewhere and get a \(\fbox{contradiction}\). QED". Better than a proof by contradiction is a constructive proof.

15.2.5 A Non-Constructive Proof of Rational Powers of Irrational Numbers

Here is a non-constructive proof which is amazing:

Theorem 2. There exist two irrational \(x\), \(y\) such that \(x^{y}\) is rational.

Proof. There are two possibilities. Either \(z=\sqrt{2}^{\sqrt{2}}\) is irrational or not. In the first case, we have found an example where \(x=y=\sqrt{2}\). In the second case, take \(x=z\) and take \(y=\sqrt{2}\). Now \(x^{y}=\sqrt{2}^{2}=2\) is rational and we have an example. ◻

15.2.6 Exploring Curvature and the Hopf Umlaufsatz

The second proof technique we see today is a deformation argument. To illustrate it, take a closed \(C^{2}\) curve in \(\mathbb{R}^{2}\) without self intersections. We have defined its curvature \(\kappa(t)\) already. For curves in \(\mathbb{R}^{2}\), define the signed curvature \(K(t)\). If the curve parametrized so that \(|r^{\prime}(t)|=1\) and \(T(t)=[\cos (\alpha(t)), \sin (\alpha(t))]\), then \(K(t)=\alpha^{\prime}(t)\). Note that \[\kappa(t)=|T^{\prime}(t)|=\big|[-\sin (\alpha(t)), \cos (\alpha(t))] \alpha^{\prime}(t)\big|=|K(t)|.\] Now if we have a curve \(r:[a, b] \rightarrow \mathbb{R}^{2}\), we can define the total curvature as \(\int_{a}^{b} K(t) \,d t\). By the fundamental theorem of calculus, this total curvature is the change of the angle \(\alpha(b)-\alpha(a)\). Now, if the curve is closed, the initial and final angles have to differ by a multiple of \(2 \pi\). The Hopf Umlaufsatz tells that

Theorem 3. The total curvature of a simple closed curve is \(2 \pi\) or \(-2 \pi\).

Figure 3. Four simple closed curves for which it is not obvious that the total curvature is \(2 \pi\).

Problem C:

  1. Why is the total curvature not always \(2 \pi\)?
  2. Formulate out what happens in in Figure (15.4).
Figure 4. Hopf’s deformation proof: each picture shows the line through \(r(s)\), \(r(t)\) and to the right the parameter \((s, t)\). In the left column, where \(s=t\), we deal with the tangent turning. We have to show it turns by \(2 \pi\). The next columns deform the situation where the path through the parameter square is changed. In the very right column, we twice turn the segment by \(\pi\), in total \(2 \pi\).

EXERCISES

Exercise 1. Prove by contradiction that \(\sqrt{12}\) is irrational.

Exercise 2. Prove by contradiction that \(\log_{10}(2)\) is irrational. \(\log_{10}\) is the logarithm with respect to the base \(10\).

Exercise 3. Prove by contradiction that there are infinitely many primes of the form \(4 k-1\).

Hint: If \(p_{i}\) are of the form \(4 k-1\) then \(4 \prod_{j} p_{i}-1\) is again of the form \(4 k-1\).

Exercise 4. Verify the Hopf Umlaufsatz for a circle of radius \(5\), where \[r(t)=\left[\begin{array}{c}5 \cos (t) \\ 5 \sin (t)\end{array}\right].\] Optional: what does the Umlaufsatz say for a triangle?

Figure 5. Can you adapt the Hopf Umlaufsatz for triangles?

Exercise 5. There is a variant of proof by contradiction which is proof by infinite descent. It was used in proving a special case of Fermat’s Last Theorem. This special result tells that the equation \(r^{2}+s^{4}=t^{4}\) has no solution with positive \(r\), \(s\), \(t\). Look up and write down the proof of this theorem.

Figure 6. Pierre de Fermat: cropped from Foto by Didier Descouens: showing the Monument to Pierre de Fermat by Alexandre Falguière in Beaumont-de-Lomagne, Tarn-et-Garonne France.
  1. For more explanation, see https://www.youtube.com/watch?v=Ih16BIoR9eM↩︎