Constraints

 

20.1 INTRODUCTION

20.1.1 Gradients for Optimal Solutions with Constraints

There is rarely a "free lunch". If we want to maximize a quantity, we often have to work with constraints. Obstacles might prevent us to change the parameters arbitrarily. The gradient can still be used as a guiding principle. While we can not achieve \(\nabla f\) to be zero, we can look for points where the gradient is perpendicular to the constraint. This gives us an optimal point under the confinement. If you hike on a path in the mountains, you often reach a local maximum without being on top of the mountain. What happens at such points \(x\) is that \(\nabla f(x)\) is perpendicular to the curve meaning that \(\nabla f(x)\) is parallel to \(\nabla g(x)\).

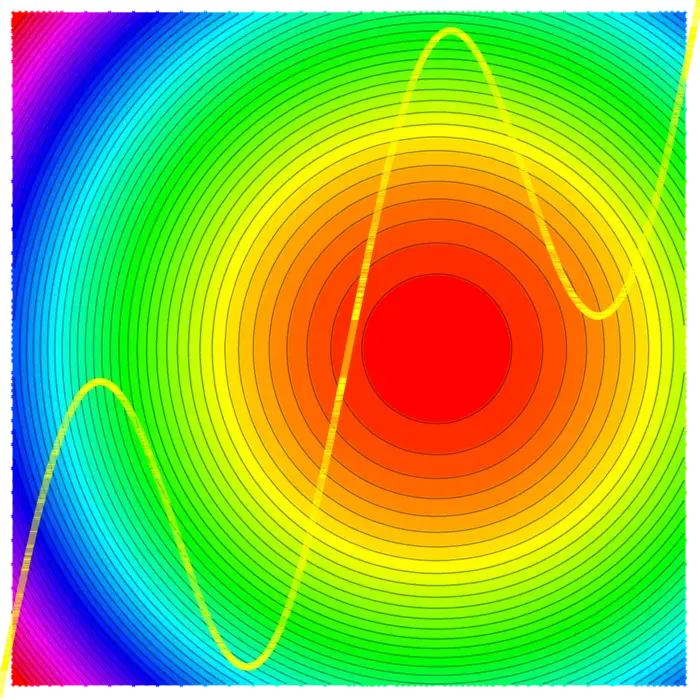
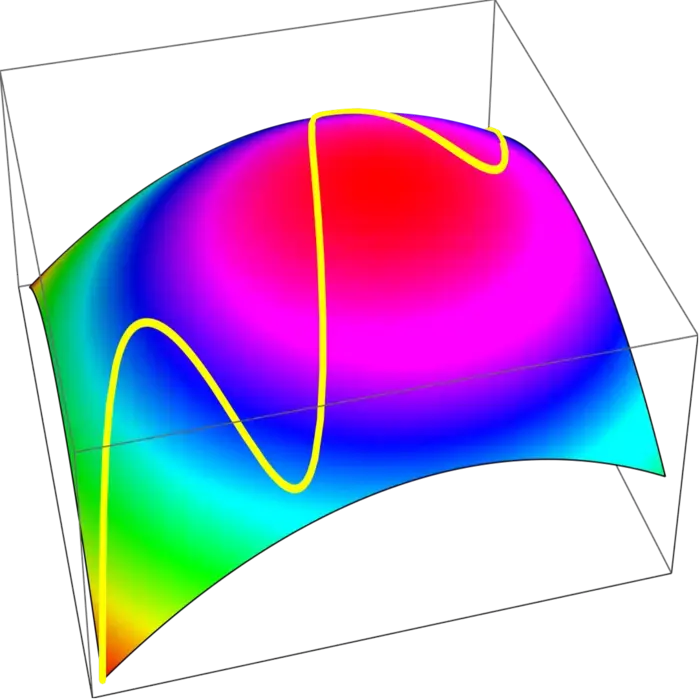
Figure 1. The situation, where a function \(f(x, y)\) is optimized along a curve \(g(x, y)=c\) is a frame-work which can be tackled with Lagrange. The condition of being maximal means that the gradient of \(f\) is perpendicular to the curve. This means that the gradients of \(f\) and \(g\) are parallel. \(\nabla f=\lambda \nabla g\).

20.1.2 Lagrange’s Magic: Many Constraints, One Solution

The method of Lagrange is much more general. We can work with arbitrary many constraints and still use the same principle. The gradient of \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) is then perpendicular to the constraint surface which means that is a linear combination of the gradients of all the \(m\) constraints: these are \(n\) equations \(\nabla f=\sum_{j=1}^{m} \lambda_{j} \nabla g_{j}\) because the vectors have \(n\) components. Together with the \(m\) equations \(g_{j}=c_{j}\) we have \(n+m\) equations for \(n+n\) variables \(x_{1}, \ldots, x_{n}\), \(\lambda_{1}, \ldots, \lambda_{m}\).

20.2 LECTURE

20.2.1 Finding the Maximum in Confined Spaces

If we want to maximize a function \(f: \mathbb{R}^{m} \rightarrow \mathbb{R}\) on the constraint \[S=\left\{x \in \mathbb{R}^{m} \mid g(x)=c\right\},\] then both the gradients of \(f\) and \(g\) matter. We call two vectors \(v\), \(w\) parallel if \(v=\lambda w\) or \(w=\lambda v\) for some real \(\lambda\). The zero vector is parallel to everything. Here is a variant of Fermat:

Theorem 1. If \(x_{0}\) is a maximum of \(f\) under the constraint \(g=c\), then \(\nabla f(x_{0})\) and \(\nabla g(x_{0})\) are parallel.

Proof. By contradiction: assume \(\nabla f(x_{0})\) and \(\nabla g(x_{0})\) are not parallel and \(x_{0}\) is a local maximum. Let \(T\) be the tangent plane to \(S=\{g=c\}\) at \(x_{0}\). Because \(\nabla f(x_{0})\) is not perpendicular to \(T\) we can project it onto \(T\) to get a non-zero vector \(v\) in \(T\) which is not perpendicular to \(\nabla f\). Actually the angle between \(\nabla f\) and \(v\) is acute so that \(\cos (\alpha)>0\). Take a curve \(r(t)\) in \(S\) with \(r(0)=x_{0}\) and \(r^{\prime}(0)=v\). We have \[\begin{aligned} d / d t f(r(0))&=\nabla f(r(0)) \cdot r^{\prime}(0)\\ &=|\nabla f(x_{0})||v| \cos (\alpha)\\ &>0. \end{aligned}\] By linear approximation, we know that \(f(r(t))>f(r(0))\) for small enough \(t>0\). This is a contradiction to the fact that \(f\) was maximal at \(x_{0}=r(0)\) on \(S\). ◻

Figure 2. A Lagrange problem

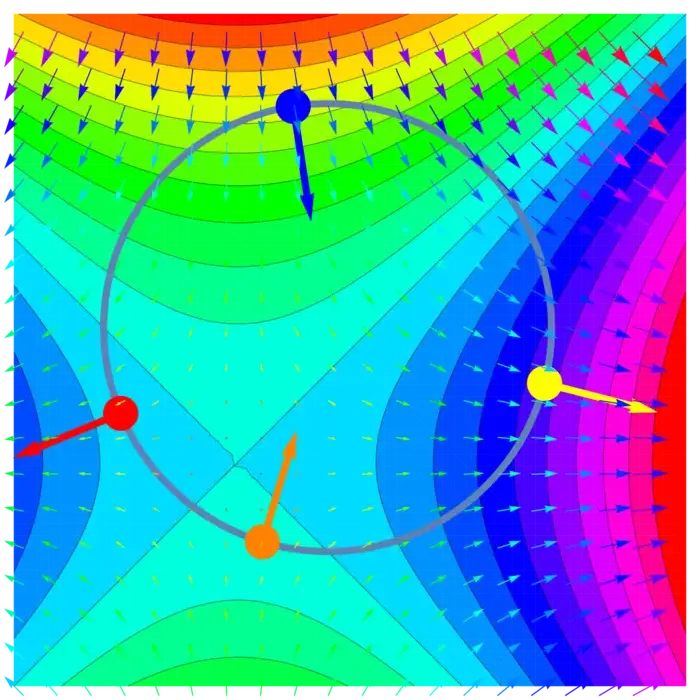
20.2.2 Exploring Lagrange Multipliers and Necessary Conditions

This immediately implies: (distinguish \(\nabla g \neq 0\) and \(\nabla g=0\))

Theorem 2. For a maximum of \(f\) on \(S=\{g=c\}\) either the Lagrange equations \(\nabla f(x_{0})=\lambda \nabla g(x_{0})\), \(g=c\) hold, or then \(\nabla g(x_{0})=0\), \(g=c\).

For functions \(f(x, y), g(x, y)\) of two variables, this means we have to solve a system with three equations and three unknowns: \[\begin{aligned} f_{x}(x_{0}, y_{0}) & =\lambda g_{x}(x_{0}, y_{0}) \\ f_{y}(x_{0}, y_{0}) & =\lambda g_{y}(x_{0}, y_{0}) \\ g(x, y) & =c \end{aligned}\]

20.2.3 Finding the True Maximum

To find a maximum, solve the Lagrange equations and add a list of critical points of \(g\) on the constraint. Then pick a point where \(f\) is maximal among all points. We don’t bother with a second derivative test. But here is a possible statement: \[\frac{d^{2}}{d t^{2}} D_{t v} D_{t v} f(x_{0})\big|_{t=0}<0\] for all \(v\) perpendicular to \(\nabla g(x_{0})\), then \(x_{0}\) is a local maximum.

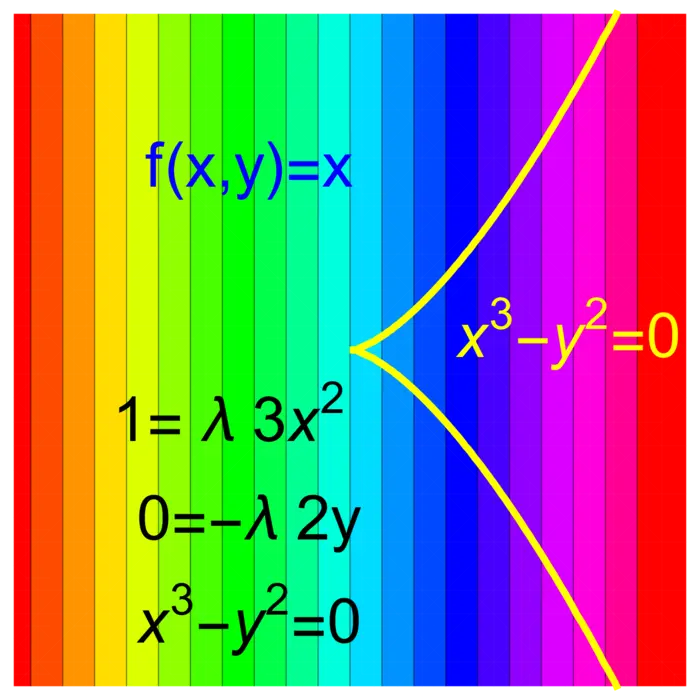
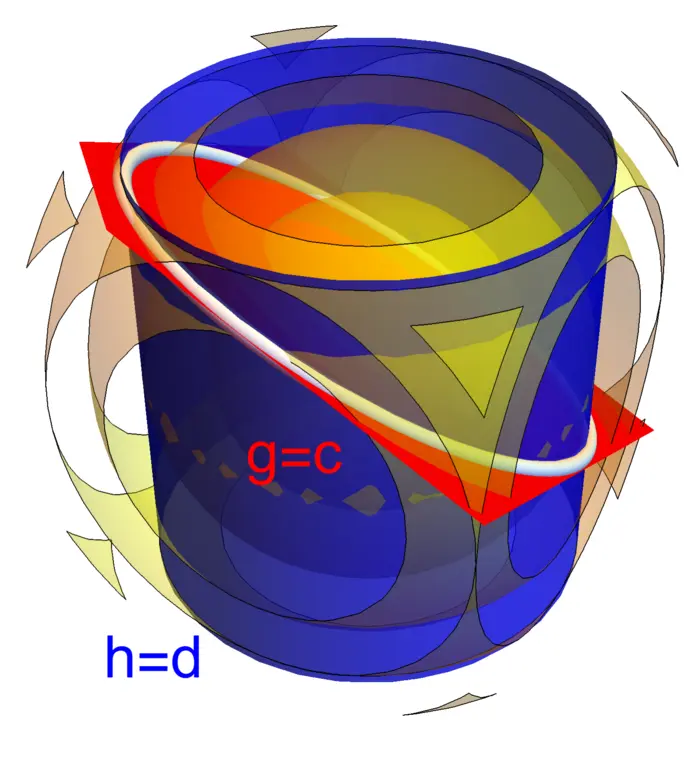
Of course, the case of maxima and minima are analog. If \(f\) has a maximum on \(g=c\), then \(-f\) has a minimum at \(g=c\). We can have a maximum of \(f\) under a smooth constraint \(S=\{g=c\}\) without that the Lagrange equations are satisfied. An example is \(f(x, y)=x\) and \(g(x, y)=x^{3}-y^{2}\) shown in Figure (20.3).

Figure 3. An example of a function, where the Lagrange equations do not give the minimum, here \((0,0)\). It is a case, where \(\nabla g=0\).

20.2.4 Lagrange’s Climb: Maximizing with Multiple Constraints

The method of Lagrange can maximize functions \(f\) under several constraints. Lets show this in the case of a function \(f(x, y, z)\) of three variables and two constraints \(g(x, y, z)=c\) and \(h(x, y, z)=d\). The analogue of the Fermat principle is that at a maximum of \(f\), the gradient of \(f\) is in the plane spanned by \(\nabla g\) and \(\nabla h\). This leads to the Lagrange equations for \(5\) unknowns \(x, y, z, \lambda, \mu\). \[\begin{aligned} f_{x}(x_{0}, y_{0}, z_{0}) & =\lambda g_{x}(x_{0}, y_{0}, z_{0})+\mu h_{x}(x_{0}, y_{0}, z_{0}) \\ f_{y}(x_{0}, y_{0}, z_{0}) & =\lambda g_{y}(x_{0}, y_{0}, z_{0})+\mu h_{y}(x_{0}, y_{0}, z_{0}) \\ f_{z}(x_{0}, y_{0}, z_{0}) & =\lambda g_{z}(x_{0}, y_{0}, z_{0})+\mu h_{z}(x_{0}, y_{0}, z_{0}) \\ g(x, y, z) & =c \\ h(x, y, z) & =d \end{aligned}\]

For example, if \[\begin{aligned} f(x, y, z)&=x^{2}+y^{2}+z^{2},\\ g(x, y, z)&=x^{2}+y^{2}=1,\\ h(x, y, z)&=x+y+z=4, \end{aligned}\] then we find points on the ellipse \(g=1\), \(h=4\) with minimal or maximal distance to \(0\).

Figure 4. We see a situation where we try to maximize a function \(f\) under two constraints. In this case the intersection \(g=c\), \(h=d\) is an ellipse.

20.3 EXAMPLES

Example 1. Problem: Minimize \(f(x, y)=x^{2}+2 y^{2}\) under the constraint \(g(x, y)=x+y^{2}= 1\).
Solution: The Lagrange equations are \(2 x=\lambda\), \(4 y=\lambda 2 y\). If \(y=0\) then \(x=1\). If \(y \neq 0\) we can divide the second equation by \(y\) and get \(2 x=\lambda\), \(4=\lambda 2\) again showing \(x=1\). The point \(x=1\), \(y=0\) is the only solution.

Example 2. Problem: Which cylindrical soda can of height \(h\) and radius \(r\) has minimal surface \(A\) for fixed volume \(V\)?
Solution: We have \(V(r, h)=h \pi r^{2}=1\) and \(A(r, h)=\) \(2 \pi r h+2 \pi r^{2}\). With \(x=h \pi\), \(y=r\), you need to optimize \(f(x, y)=2 x y+2 \pi y^{2}\) under the constrained \(g(x, y)=x y^{2}=1\). We will do that in class.

Example 3. Problem: If \(0 \leq p_{k} \leq 1\) is the probability that a dice shows \(k\), then we have \(g(p)=p_{1}+p_{2}+\cdots+p_{6}=1\). This vector \(p\) is called a probability distribution. The Shannon entropy of \(p\) is defined as \[\begin{aligned} S(p)&=-\sum_{i=1}^{6} p_{i} \log (p_{i})\\ &=-p_{1} \log (p_{1})-p_{2} \log (p_{2})-\cdots-p_{6} \log (p_{6}) \end{aligned}\]

Find the distribution \(p\) which maximizes entropy \(S\).
Solution: \[\nabla f=\big(-1-\log (p_{1}), \ldots,-1-\log (p_{n})\big), \quad \nabla g=(1, \ldots, 1).\] The Lagrange equations are \[-1-\log (p_{i})=\lambda, \quad p_{1}+\cdots+p_{6}=1,\] from which we get \(p_{i}=e^{-(\lambda+1)}\). The last equation \[1=\sum_{i} \exp (-(\lambda+1))=6 \exp (-(\lambda+1))\] fixes \(\lambda=-\log (1 / 6)-1\) so that \(p_{1}=p_{2}=\cdots=p_{6}=1 / 6\). It is the fair dice that has maximal entropy. Maximal entropy means least information content.

Example 4. Assume that the probability that a physical or chemical system is in a state \(k\) is \(p_{k}\) and that the energy of the state \(k\) is \(E_{k}\). Nature minimizes the free energy \[F(p_{1}, \ldots, p_{n})=-\sum_{i}\left[p_{i} \log (p_{i})-E_{i} p_{i}\right]\] if the energies \(E_{i}\) are fixed. The probability distribution \(p_{i}\) satisfying \(\sum_{i} p_{i}=1\) minimizing the free energy is called a Gibbs distribution. Find this distribution in general if \(E_{i}\) are given.
Solution: \[\nabla f=(-1-\log (p_{1})-E_{1}, \ldots,-1-\log (p_{n})-E_{n}), \quad \nabla g=(1, \ldots, 1).\] The Lagrange equation are \(\log (p_{i})=-1-\lambda-E_{i}\), or \(p_{i}=\exp (-E_{i}) C\), where \(C=\exp(-1-\lambda)\). The constraint \(p_{1}+\cdots+p_{n}=1\) gives \(C\big(\sum_{i} \exp \left(-E_{i}\right)\big)=1\) so that \(C=1 /\left(\sum_{i} e^{-E_{i}}\right)\). The Gibbs solution is \(p_{k}=\exp (-E_{k}) / \sum_{i} \exp (-E_{i})\).1

Example 5. If \(f\) is a quadratic function on \(\mathbb{R}^{m}\) and \(g\) is linear that is \(f(x)=B x \cdot x / 2\) with \(B \in M(m, m)\) and if the constraint \(g(x)=A x=c\) is linear \(A \in M(1, m)\), then \(\nabla f(x)=B x\) and \(\nabla g(x)=A^{T}\). Lets call \(b=A^{T} \in M(m, 1) \sim \mathbb{R}^{m}\). The Lagrange equations are then \(B x=\lambda b\), \(A x=c\). We see in general that for quadratic \(f\) and linear \(g\), we end up with a linear system of equations.

Example 6. Related to the previous remark is the following observation. It is often possible to reduce the Lagrange problem to a problem without constraint. This is a point of view often taken in economics. Let us look at it in dimension \(2\), where we extremize \(f(x, y)\) under the constraint \(g(x, y)=0\). Define \(F(x, y, \lambda)=f(x, y)-\lambda g(x, y)\). The Lagrange equations for \(f, g\) are now equivalent to \(\nabla F(x, y, \lambda)=0\) in three dimensions.

EXERCISES

Exercise 1. Find the cylindrical basket which is open on the top has has the largest volume for fixed area \(\pi\). If \(x\) is the radius and \(y\) is the height, we have to maximize \(f(x, y)=\pi x^{2} y\) under the constraint \[g(x, y)=2 \pi x y+\pi x^{2}=\pi.\] Use the method of Lagrange multipliers.

Exercise 2. Given a \(n \times n\) symmetric matrix \(B\), we look at the function \(f(x)=x \cdot B x\). and look at extrema of \(f\) under the constraint that \(g(x)=x \cdot x=1\). This leads to an equation \[B x=\lambda x.\] A solution \(x\) is called an eigenvector. The Lagrange constant \(\lambda\) is an eigenvalue. Find the solutions to \(B x=\lambda x\), \(|x|=1\) if \(B\) is a \(2 \times 2\) matrix, where \[f(x, y)=a x^{2}+(b+c) x y+d y^{2}, \quad g(x, y)=x^{2}+y^{2}.\] Then solve the problem with \(a=4\), \(b=1\), \(c=1\), \(d=4\).

Exercise 3. Which pyramid of height \(h\) over a square \([-a, a] \times[-a, a]\) with surface area is \(4 a \sqrt{h^{2}+a^{2}}+4 a^{2}=4\) has maximal volume \(V(h, a)=\) \(4 h a^{2} / 3\)? By using new variables \((x, y)\) and multiplying \(V\) with a constant, we get to the equivalent problem to maximize \(f(x, y)=y x^{2}\) over the constraint \[g(x, y)=x \sqrt{y^{2}+x^{2}}+x^{2}=1.\] Use the later variables.

Exercise 4. Motivated by the Disney movie "Tangled", we want to build a hot air balloon with a cuboid mesh of dimension \(x\), \(y\), \(z\) which together with the top and bottom fortifications uses wires of total length \[g(x, y, z)=6 x+6 y+4 z=32.\] Find the balloon with maximal volume \(f(x, y, z)=x y z\).

Exercise 5. A solid bullet made of a half sphere and a cylinder has the volume \(V=2 \pi r^{3} / 3+\pi r^{2} h\) and surface area \(A=2 \pi r^{2}+2 \pi r h+\pi r^{2}\). Doctor Manhattan designs a bullet with fixed volume and minimal area. With \(g=3 V / \pi=1\) and \(f=A / \pi\) he therefore minimizes \(f(h, r)=3 r^{2}+2 r h\) under the constraint \[g(h, r)=2 r^{3}+3 r^{2} h=1.\] Use the Lagrange method to find a local minimum of \(f\) under the constraint \(g=1\).

Appendix: Data illustration: Cobb Douglas

20.3.1 Cobb-Douglas: A Formula for Economic Growth

The mathematician and economist Charles W. Cobb at Amherst college and the economist and politician Paul H. Douglas who was also teaching at Amherst, found in 1928 empirically a formula \(F(K, L)=L^{\alpha} K^{\beta}\) which fits the total production \(F\) of an economic system as a function of the capital investment \(K\) and the labor \(L\). The two authors used logarithms variables and assumed linearity to find \(\alpha, \beta\). Below are the data normalized so that the date for year 1899 has the value \(100\).

Year\(K\)\(L\)\(P\)
1899100100100
1900107105101
1901114110112
1902122118122
1903131123124
1904138116122
1905149125143
1906163133152
1907176138151
1908185121126
1909198140155
1910208144159
1911216145153
1912226152177
1913236154184
1914244149169
1915266154189
1916298182225
1917335196227
1918366200223
1919387193218
1920407193231
1921417147179
1922431161240
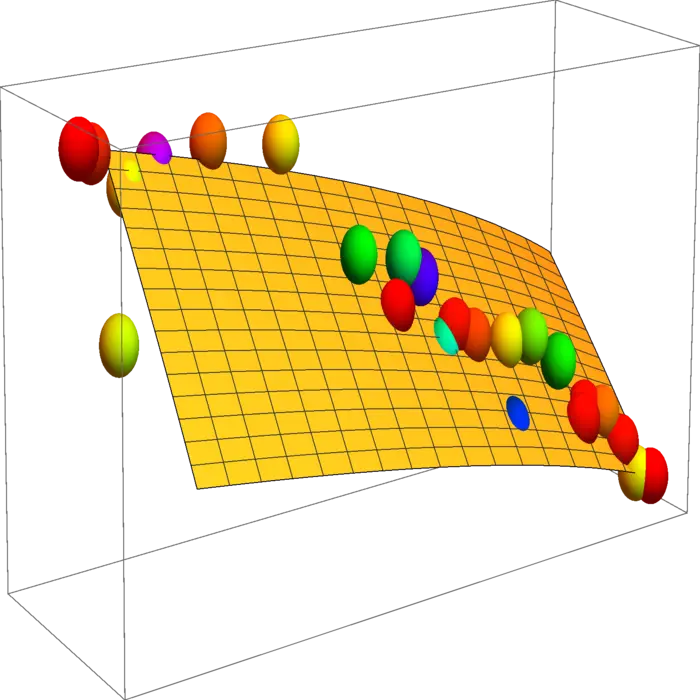
Figure 5. The graph of \(F(L, K)=L^{3 / 4} K^{1 / 4}\) fits pretty well that data set. You can see in the data that there is an out-layer.

20.3.2 Visualizing Production Limits

Assume that the labor and capital investment are bound by the additional constraint \(G(L, K)=L^{3 / 4}+K^{1 / 4}=50\). (This function \(G\) is unrelated to the function \(F(L, K)\) as we are in a Lagrange problem.) Where is the production \(P\) maximal under this constraint? Plot the two functions \(F(L, K)\) and \(G(L, K)\).

  1. This example is from Rufus Bowen, Lecture Notes in Math, 470, 1978↩︎