A Visit by Archimedes

 

27.1 INTRODUCTION

27.1.1 A Meeting of Minds Across Millennia

Drum rolls... Here is Archimedes (287 BC - 212 BC). He is considered the father of integral calculus. He is also considered a "polymath", somebody who mastered and innovated several topics: mathematics, physics, engineering and astronomy.

Figure 1. Archimedes working on some exam problem!

27.2 SEMINAR

27.2.1 Welcome, Archimedes!

In this review lecture we have the honor to have Archimedes as a special guest. Before the event, we talked to him using a technology called "quantum forward tunneling" which allows to interact with part of the past without running into a causality paradox. The actual Archimedes did not know about the interview. It is his "quantum spirit" which does it for us. How does it work? Quantum space-time produces sometimes tiny wormhole constellations in which a wave function can be trapped. By harvesting many of those trapped waves, we can rebuild and interact with an object or person from a previous time. The so established "time tunnel" is sustainable only for a short time as the trapped waves will fade within a half an hour. It is enough time however for a short interview. We take the opportunity and ask him about his theorems.

27.2.2 Eureka! Unveiling the Secrets of the Sphere

Math 22b: What a pleasure to have you here. Welcome!
Archimedes: I’m glad to find myself in this lovely place. It must be a dream. I don’t recognize the town but it feels like a ’Alexandria in the future’.
Math 22b: yes, it is also a hot spot for science, but there are many now. We are eager to learn a bit about your proof expertise.

27.2.3 Archimedes and the Wooden Models: Unveiling Volume Ratios

Math 22b: What result of yours do you consider the most important one?
Archimedes: Definitely the formula for the volume of the sphere!
Math 22b: Why?
Archimedes: It was much harder to get this than the circumference of the circle or the surface area of the sphere. It was also harder to test the result experimentally.
Math 22b: How did you measure?
Archimedes: We build wood models of cylinders, cones and spheres of the same base radius and height and measured their volume ratios.

Problem A: Explain how Archimedes can using wooden models measure their volumes. If you don’t know, take a bath. Given a cylinder \(C\), a cone \(O\) and a sphere \(S\) of base length \(1\). What ratios \(|C| /|S|\), \(|O| /|S|\) do the measurements show?

27.2.4 The Slicing Trick: A Historical First Proof for the Sphere’s Volume?

Math 22b: Was the comparison of the sphere with the complement of a cone in the cylinder historically the first proof?
Archimedes: The relation had been conjectured before. It had been suspected that the ratio between the volume of a sphere and the volume of a cylinder is the fraction \(2 / 3\) but nobody had been able to prove this relation before I could see the slicing trick.

Problem B: Explain why slicing the unit sphere at height \(z\) gives the same area as a ring of radius \(1\) in which a hole of size \(z\) has been has been drilled.

27.2.5 A Discovery in the Tub

Math 22b: Do you remember the precise moment, when the discovery stuck?
Archimedes: I don’t recall directly but it must have been one of these "hot tub ideas".

27.2.6 Archimedes and the Circle: A Journey to Pi

Math 22b: This discovery must have occurred after you got the circle circumference computed. How difficult was the later?
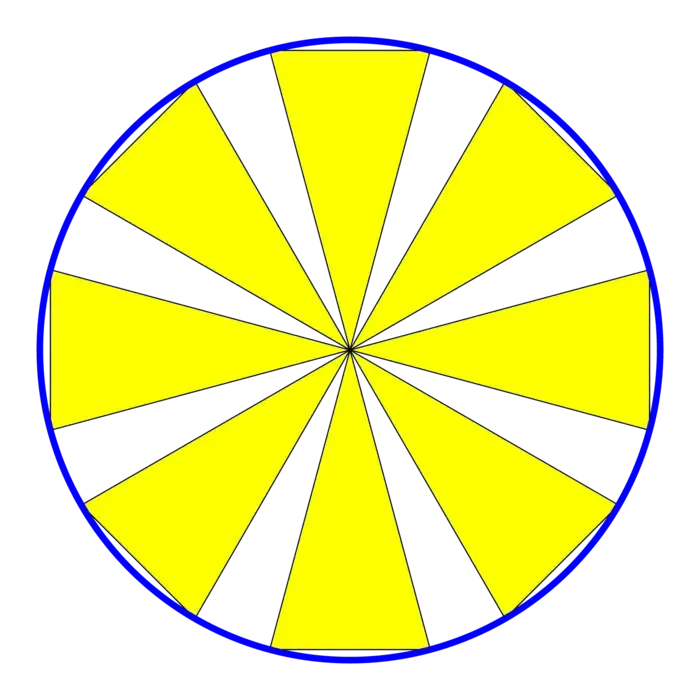
Archimedes: also this needed some time. It emerged pretty early that the circumference is somehow proportional to the radius. The measurement of the constant was then a bit trickier even so it remained open what fraction it is. \(22/7\) was close. I got first the diameter/area ratio. I did that using the following picture.

Problem B: How does the picture below prove that the area \(A\), radius \(R\) and diameter \(D\) of a circle satisfies \(2 A=R D\)? How can you make this precise as in reality the circular sector does not have the same area as the triangle. (Hint: you can use modern tools like L’Hôpital’s rule if you like).

Figure 2. The circle proof.

27.2.7 The Curious Hoof: Unraveling its Volume

Math 22b: We also wonder about your computation of the volume of the "hoof" which is the solid bound by the cylinder \(x^{2}+y^{2}=1\) and \(z=x\) and \(z=0\).
Archimedes: I don’t recognize the symbols you just spelled out but I know what object you are talking about. It was exciting to see a solid bound partly by round parts to have a rational volume, which is \(2\) third of the height. One can see that the result is \(2 / 3\) in various ways.

Problem C:

  1. Take a hoof of height \(1\) and cut in triangular pieces which are obtained if \(y\) is constant. Show that the area of the triangle is \((1-y^{2}) / 2\) and conclude from this the volume is \(2 / 3\).
  2. Cut the same hoof into rectangular pieces which are obtained if \(x\) is constant. Show that the area of the rectangle is \((1-x^{2})\) and conclude that the volume is \(2 / 3\).

27.2.8 Cylinders and Spheres: Relating Surface Areas

Math 22b: Also very impressive is your computation of the surface area of the sphere by relating it with the surface area of a cylinder. What was the intuition there?
Archimedes: Actually, a drawing which is accurate enough shows this pretty well. As both situations have circular symmetry, we only need to understand what happens with the lengths on a sphere when it is projected on the cylinder. There are similar triangles. Take a stick of some length and place it onto the sphere pointing to the north pole. As it gets closer to the pole and its height-length is one half of the actual length. then the radius of that position is also half etc. As the area of a small sphere strip is height times radius times about \(22 / 7\), this is also the area of a cylinder. In the sphere case, the factor one-half is applied to the radius. In the cylinder case it is applied to the height.

Problem C: Explain this in more modern terms. We have a unit sphere and a cylinder of radius \(1\). Look what the surface area of a strip \(z\), \(z+d z\) is in both cases. You can use the spherical angle \(\phi\) which you know from spherical coordinates.

27.2.9 The Birth of Functions: Archimedes Enters a New World

Math 22b: A last question: What is a function in mathematics?
Archimedes: I don’t know this expression: for me, mathematics deals with geometric objects and numbers which characterize those objects like length, area or volume.
Math 22b: we interpret your formula for the volume of a sphere as \(V(r)=4 \pi r^{3} / 3\) which is a rule assigning to the radius \(r\) a number. We also have rules which tell how to compute rates of change. For the function \(V(r)\) for example, its rate of change is \(4 \pi r^{2}\), the surface area of the sphere. The reason is that if we decrease the radius by a small unit, then this essentially means taking away a layer of area \(4 \pi r^{2}\).
Archimedes: This is cool. Let me see: does this also work for the area and circumference of a disc?
Math 22b: Certainly. Go ahead.
Archimedes: Well, with this new language, we would say that a disc of radius \(r\) is \(f(r)=\pi r^{2}\). I assume that for any integer \(n\) the rate of change of \(r^{n}\) is \(n r^{n-1}\).
Math 22b: Yes, that is correct.
Archimedes: In that case the rate of change of \(\pi r^{2}\) is \(2 \pi r\) and indeed this is my formula for the circumference of a circle. This is "Phaidros".

27.2.10 A Meeting of Minds Ends

Math 22b: Thank you very much for the interview. It will inspire us for the second midterm exam. Maybe you can visit and take the exam on Tuesday or review on Sunday?
Archimedes: ’It will be my pleasure."

EXERCISES

Exercise 1. Find a solid which has the property that if you project it on the \(x y\)-plane it is a half circle, if you project it on the \(y z\) plane it is a triangle and if you project it onto the \(x z\)-plane, it is a rectangle.

Exercise 2. There are regions in the plane which have the property that their thickness is constant \(1\) but which are not circles. Find some. These curves are also known under the name curve of constant width.

Exercise 3. There is a beautiful theorem of Pappus which gives the formula of a solid obtained by taking all points in distance \(d\) from a given curve \(r(t)\) provided the thickened curve does not intersect: the formula is \(L \pi d^{2}+4 \pi d^{3} / 3\), where \(L\) is the length of the curve. Archimedes designed a spiral pump in which a spiral \(r(t)=[10 \cos (t), 10 \sin (t), t]\) plays an important role. Assume \(0 \leq t \leq 100 \pi\), what is the volume of the solid consisting of all points in distance \(1\) to the curve? You just need to compute that volume and not prove the formula.

Exercise 4. Let \(A\) be the solid obtained by intersecting three perpendicular solid cylinders \(x^{2}+y^{2} \leq 1\), \(x^{2}+z^{2} \leq 1\), \(y^{2}+z^{2} \leq 1\). What is its volume?

Exercise 5. Archimedes had another picture for the volume of a sphere. It is seen in the picture above to the right and was mentioned in lecture \(24\). Please explain in your own words.

Figure 3. The "Archimedes screw" and another sphere proof.
Figure 4. The intersection of three cylinders is a classical problem which Archimedes solved already.