Vectors

In physics, one often refers to a vector as a quantity with length and direction, and represents it by an arrow ↗. This can hardly be called a definition, since almost all the terms used are undefined. To make it precise, observe that the “arrow” is determined if we specify: a) its initial point (the tail of the arrow); b) its end point (the head of the arrow).

Thus we are led to define a vector in n-space to be an ordered pair of points in n-space, therefore an ordered pair of n-tuples of numbers. The first point will be called the initial point, the second the end point.

It is likewise customary to regard two vectors as equal if they have the same length and the same direction, thus if their “arrows” satisfy these conditions. Let us look at this in 2-space:

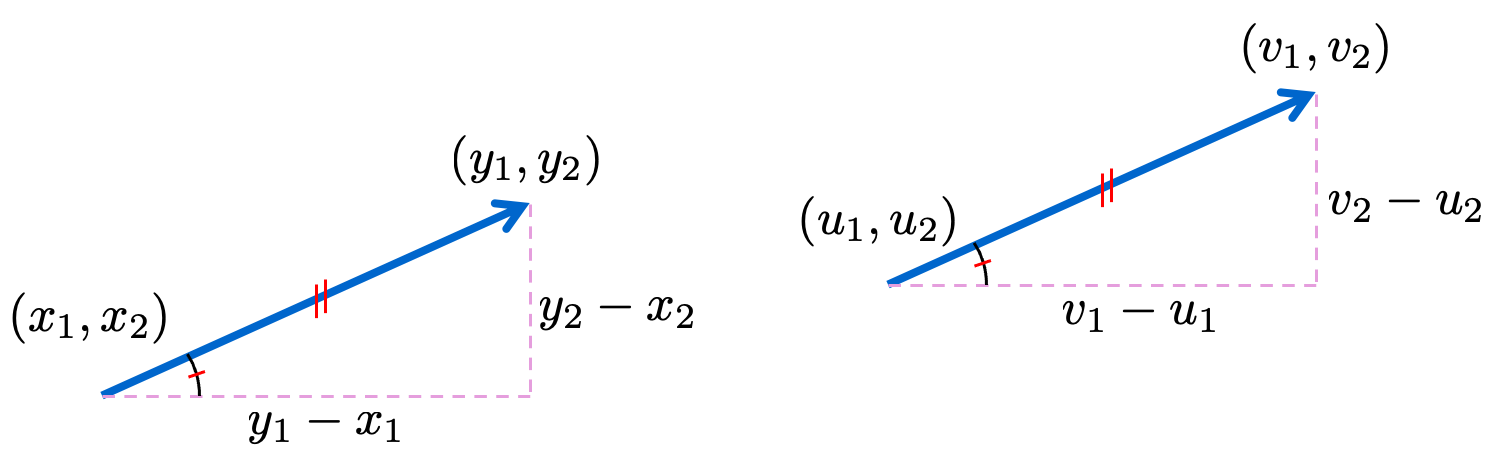
If these two vectors are to be equal in this sense, it means that the two right triangles shown have their hypotenuse and one acute angle equal, therefore are congruent. In particular, the other sides are equal, i.e., \[ y_{1}-x_{1}=v_{1}-u_{1}, \quad y_{2}-x_{2}=v_{2}-u_{2} \]

Therefore let \[ \left(\left(x_{1}, x_{2}, \ldots, x_{n}\right), \quad\left(y_{1}, y_{2}, \ldots, y_{n}\right)\right) \] and \[ \left(\left(u_{1}, u_{2}, \ldots, u_{n}\right), \quad\left(v_{1}, v_{2}, \ldots, v_{n}\right)\right) \] be two vectors. We define them to be equal if \(y_{1}-x_{1}=v_{1}-u_{1}\), \(y_{2}-x_{2}=v_{2}-u_{2}, \ldots, y_{n}-x_{n}=v_{n}-u_{n}\)

It is seen, then, that a vector is determined to within equality by the numbers \(a_{1}=y_{1}-x_{1}, a_{2}=y_{2}-x_{2}, \ldots, a_{n}=y_{n}-x_{n}\). Thus one is led to consider a quantity which one writes as \(\left[a_{1}, a_{2}, \ldots, a_{n}\right]\). The numbers \(a_{1}, a_{2}, \ldots, a_{n}\) are called components of the vector, and the expression \(A=\left[a_{1}, a_{2}, \ldots, a_{n}\right]\) is called the free vector determined by the vector \[ \left(\left(x_{1}, x_{2}, \ldots, x_{n}\right), \quad\left(y_{1}, y_{2}, \ldots, y_{n}\right)\right] \] (or by any vector equal to this one).

Now we see how to find the free vector determined by any (ordered pair of points, and also how to find, for a given free vector and a given point, a second point such that the vector with the first point as initial point and the second as end point determines the given free vector. Given \(A=\left[a_{1}, a_{2}, \ldots, a_{n}\right]\) and initial point \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\), the desired end point is of course \(\left(x_{1}+a_{1}, x_{2}+a_{2}, \ldots, x_{n}+a_{n}\right)\). We shall often use the term located vector to refer to a pair of points, and the term “vector” will rapidly be usurped by the free vector.

The principle of addition of vectors is familiar from the parallelograms of forces used in physics. For the moment, let \(A=\left[a_{1}, a_{2}\right]\) and \(B=\left[b_{1}, b_{2}\right]\) be two vectors in 2-space. Let \(A\) be located with initial point \(\left(x_{1}, x_{2}\right)\), end point \(\left(y_{1}, y_{2}\right)\). Then we have \(y_{1}=x_{1}+a_{1}\), \(y_{2}=x_{2}+a_{2}\). We form \(A+B\) by locating \(B\) with initial point \(\left(y_{1}, y_{2}\right)\). Let \(\left(z_{1}, z_{2}\right)\) be the end point of \(B\). Then \(A+B\) is the vector determined by the pair of points \(\left(\left(x_{1}, x_{2}\right),\left(z_{1}, z_{2}\right)\right)\).

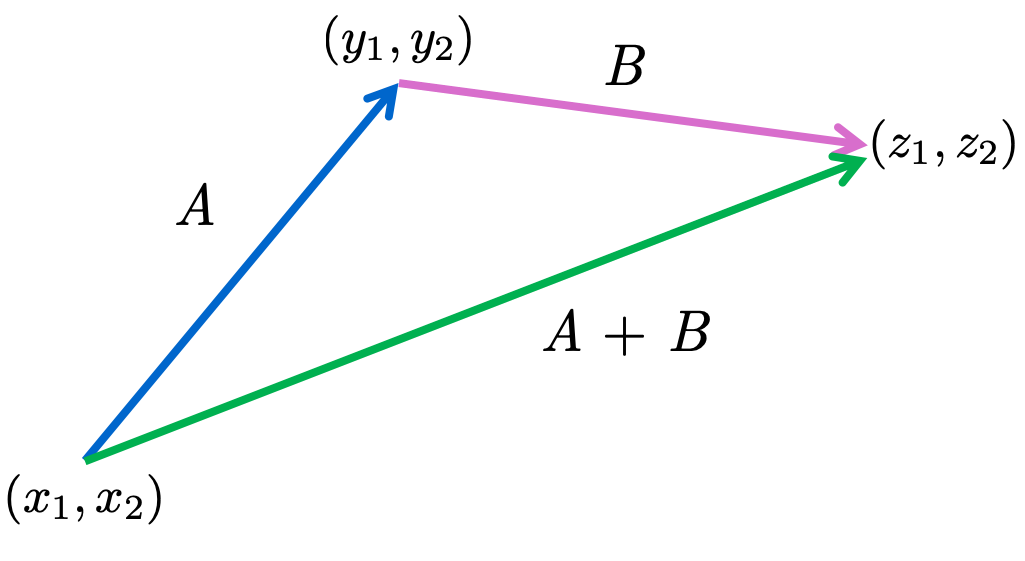
But \(z_{1}=y_{1}+b_{1}=x_{1}+a_{1}+b_{1}\), \(z_{2}=y_{2}+b_{2}=x_{2}+a_{2}+b_{2}\). Thus we have, for the free vectors, \[ A+B=\left[a_{1}+b_{1}, a_{2}+b_{2}\right] \]

This leads us to define, for arbitrary \(n\) \[ \left[a_{1}, a_{2}, \ldots, a_{n}\right]+\left[b_{1}, b_{2}, \ldots, b_{n}\right]=\left[a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{n}+b_{n}\right] \]

Please note that this is a definition, so that it requires no proof. The things that do require proof are the elementary properties of this operation, and they are given as exercises:

Let \(A=\left[a_{1}, a_{2}, \ldots, a_{n}\right]\) be a vector in n-space. We define the length of \(A\) to be the distance between its initial point and its end point when it is located at some point. Let \(A\) be located with initial point \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\), end point \(\left(y_{1}, y_{2}, \ldots, y_{n}\right)\). Then \[ y_{1}=x_{1}+a_{1}, y_{2}=x_{2}+a_{2}, \ldots, y_{n}=x_{n}+a_{n} \] The length of \(A\) is thus \[ \sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}+\ldots+\left(y_{n}-x_{n}\right)^{2}}=\sqrt{a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}} \]

From this we see that the point at which we located the vector \(A\) does not affect its length. We shall denote this number (not a vector) by \(|A|\). It is sometimes called the absolute value of A. We thus have the rule \[ |A|=\sqrt{a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}} \]

We now have means of calculating witا two categories of objects; vectors and numbers (or scalars). We shall introduce more operations, which will mix these two categories. It should, however, be remembered that the two are distinct, and that an equation \(A=2\), for instance, is as meaningless as the equation " \(x\) sheep \(=2\) oranges". Due to convention and the lack of suitable symbols, we use 0 to represent both the number zero and the zero-vector of iii). No confusion should arise from equations involving this symbol, however, because the rest of the equation will enable us to interpret the category correctly.

Next we define multiplication of vectors by numbers; if \(A=\left[a_{1}, a_{2}, \ldots, a_{n}\right]\) and \(b\) is a number, we define \[ b A=\left[b a_{1}, b a_{2}, \ldots, b a_{n}\right] \]

Note, for example, that for \(b=3\), we have \(3 A=A+A+A\), as in the case of numbers. Again some properties are given as exercises:

Consider two (located) vectors \(\left(\left(x_{1}, x_{2}\right),\left(y_{1}, y_{2}\right)\right)\) and \(\left(\left(u_{1}, u_{2}\right),\left(v_{1}, v_{2}\right)\right)\) in 2-space. When do we say that they have the same direction? In the following diagram this amounts to saying that the two angles indicated by \(\angle\) are equal; that is, they are equal in magnitude and also in sign, where they are measured counterclockwise from the positive \(x\)-axis (i.e., the horizontal axis). Thus the tangents of these angles are equal, or \[ \frac{y_{2}-x_{2}}{y_{1}-x_{1}}=\frac{v_{2}-u_{2}}{v_{1}-u_{1}} \]

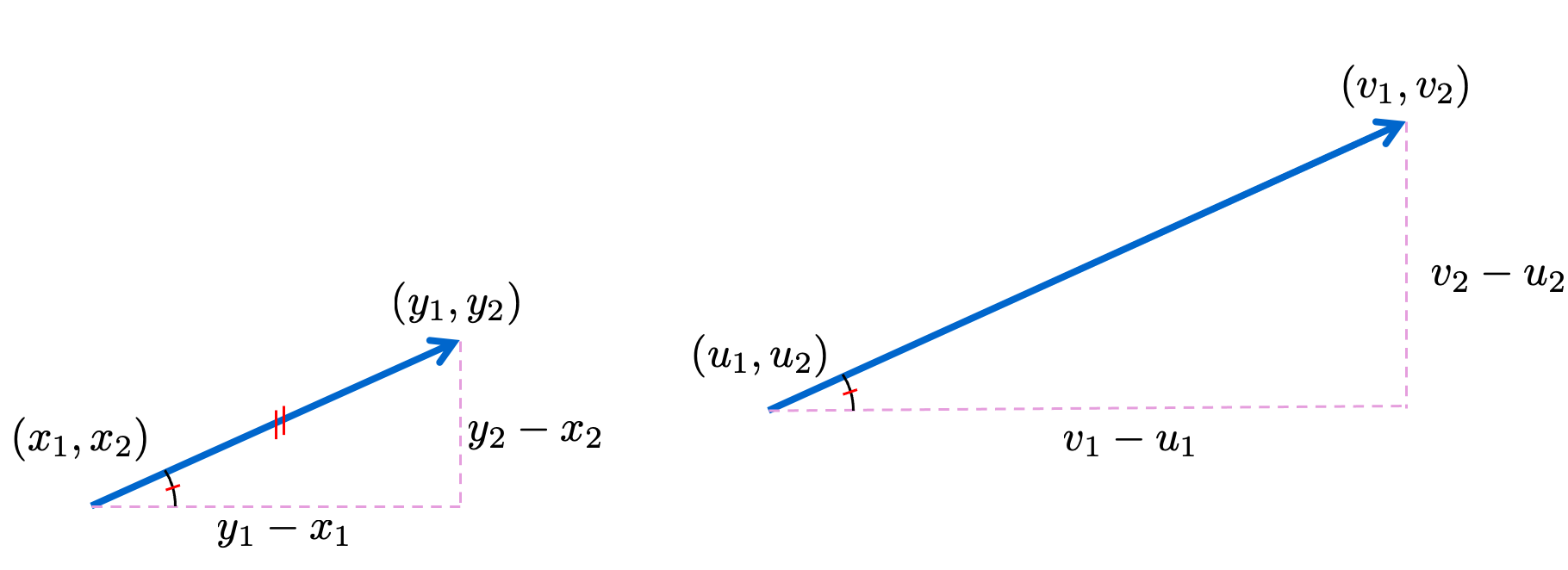
Multiplying by \[ \frac{y_{1}-x_{1}}{v_{2}-u_{2}} \] gives \[ \frac{y_{2}-x_{2}}{v_{2}-u_{2}}=\frac{y_{1}-x_{1}}{v_{1}-u_{1}} \]

Let us call this number \(b\). Then \(\left[y_{1}-x_{1}, y_{2}-x_{2}\right]=b\left[v_{1}-u_{1}, v_{2}-u_{2}\right]\). Moreover, \(b>0\) (i.e., \(b\) is positive), as is evident from the diagram. (We have assumed in performing divisions that the vectors are neither vertical nor horizontal; it is left as an exercise to show that the same type of result holds in these cases.) Thus we are led to make the following definitions:

Let \(A, B\) be non-zero vectors in n-space. We say that \(A\) and \(B\) have the same direction if \(B=b A\) for some number \(b>0\). We say that \(A\) and \(B\) have opposite directions if \(B=b A\) for some number \(b<0\). We say \(B\) is parallel to \(A\) if \(A\) and \(B\) either have the same direction or have opposite directions, therefore if \(B=b A\) for some number \(b \neq 0\). (Note that then \(A\) is also parallel to \(B\).)