Straight Lines

We have written two types of n-tuples of numbers: the n-tuple \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) is a point in n-dimensional space, while the n-tuple \(A=\left[a_{1}, a_{2}, \ldots, a_{n}\right]\) is a free vector in n-space. We now drop the notation of the square brackets and write \(A=\left(a_{1}, a_{2}, \ldots, a_{n}\right)\). The apparent confusion resulting between points and free vectors is eliminated as follows. Given the point \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\), consider the free vector determined by the located vector with initial point \((0,0, \ldots, 0)\) and end point \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\). In our new notation, this vector is also \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\). Thus one may consider the n-tuple \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) as representing a point in n-space, or as representing the vector with \((0,0, \ldots, 0)\) as initial point and this point as end point. By this identification, we may use vector addition to add objects which are ostensibly points, and then identify the resulting vector with a point.

Now we shall define a line in n-space. This is an object of a different category, neither point nor vector nor number. It is of the same category as the whole of n-dimensional space, in that it is a set, or collection of points. Thus to determine a line, we must give a rule which will enable us to decide whether a given point is on that line, or as we say, is a member of that set of points.

It is a familiar property of plane geometry that a line is determined by giving a point on it and a direction (say another line, or a vector) parallel to it. It is of course also determined by giving two distinct points on it, but this property is less convenient for our purposes. Let \(P=\left(p_{1}, p_{2}\right)\) be a point in 2-space, and let \(A=\left(a_{1}, a_{2}\right)\) be a vector, \(A \neq 0\). The question we must then answer is: Given a point \(X=\left(x_{1}, x_{2}\right)\), when is it on the line through \(P\) and parallel to \(A\) ? It is clear that the line segment \(\overline{P X}\), or, rather, the vector with initial point \(P\) and end point \(X\), must be parallel to \(A\).

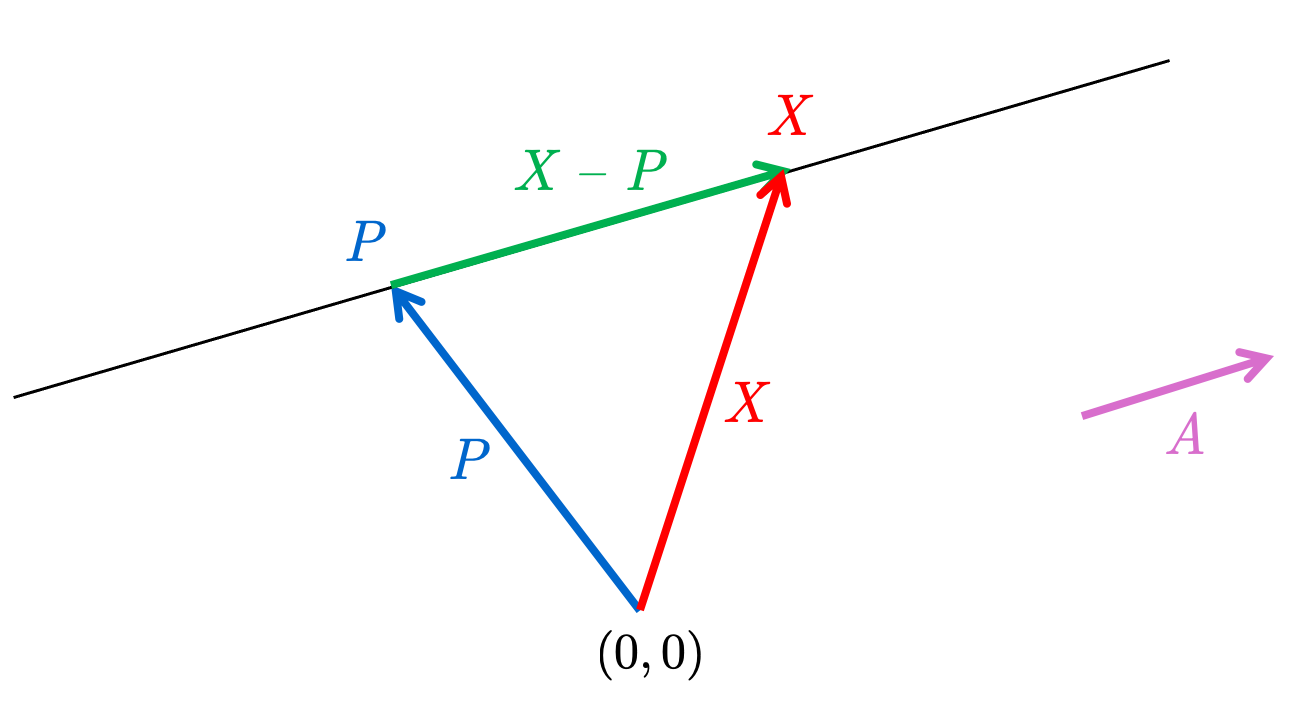
It is evident from the diagram that this vector, when added to the vector \(P\) (using our identification of points and vectors), gives the vector \(X\). Hence the vector with initial point \(P\) and end point \(X\) is the vector \(X-P\) (meaning \(X+(-P)\); see the exercises on vector addition). Thus we must have \(X-P=t A\), where \(t\) is some non-zero number. Of course, if we set \(t=0\), then \(X=P\) is on the line. Thus \(X=P+t A\), where \(t\) is some number. Moreover, if \(t\) is any number, the point \(X=P+t A\) has the property that either \(X=P\) or \(X-P\) is parallel to \(A\), i.e., \(X\) lies on the desired line.

In 2-space, this takes the form \(\left(x_{1}, x_{2}\right)=\left(p_{1}+t a_{1}, p_{2}+t a_{2}\right)\). Since \(A \neq 0\), either \(a_{1} \neq 0\) or \(a_{2} \neq 0\). Let us assume \(a_{1} \neq 0\). Then \[ x_{1}=p_{1}+t a_{1}, \quad \text { or } \quad t=\frac{x_{1}-p_{1}}{a_{1}} \] and \[ x_{2}=p_{2}+t a_{2}=p_{2}+\left(\frac{x_{1}-p_{1}}{a_{1}}\right) a_{2}=\frac{a_{2}}{a_{1}} x_{1}+\left(p_{2}-p_{1} \cdot \frac{a_{2}}{a_{1}}\right) \]

If we change our notation and write \(x\) for \(x_{1}, y\) for \(x_{2}, m\) for \(\frac{a_{2}}{a_{1}}\) and \(b\) for \(p_{2}-p_{1} \frac{a_{2}}{a_{1}}\), we obtain \[ y=m x+b \] which is the ordinary “slope-intercept” equation of a line. It means that the point ( \(x, y\) ) is on the line if and only if \(y=m x+b\), where \(m\) and \(b\) are the numbers defined above. The form \(P+t A\) for the equation of a line is customarily called the parametric form. It is used in this course because of its complete generality for all dimensions and for all vectors \(A \neq 0\).

Now let \(P=\left(p_{1}, p_{2}, \ldots, p_{n}\right)\) and \(Q=\left(q_{1}, q_{2}, \ldots, q_{n}\right)\) be two points. What is the line through \(P\) and \(Q\) ? We have a point, say \(P\), on the line, and a vector parallel to the line, namely the vector determined by the initial point \(P\) and end point \(Q\). But we have seen that this vector is just \(Q-P\). Thus the desired line is the set of points \[ X=P+t(Q-P) \] where \(t\) ranges through all numbers, or the set of points \[ X=(1-t) P+t Q \] where \(t\) ranges through all numbers.