Scalar Products

The next definition we shall make is that of scalar product, whereby two vectors are combined to give a number.

It is left as an exercise to prove the following:

1. \(A\boldsymbol{\cdot}(B+C)=A\boldsymbol{\cdot} B+A\boldsymbol{\cdot} C\)
2. \(A\boldsymbol{\cdot} B=B\boldsymbol{\cdot} A\)
3. \(a(B\boldsymbol{\cdot} C)=(a B)\boldsymbol{\cdot} C=B\boldsymbol{\cdot}(a C)\)

In particular, we define \(A^{2}=A\boldsymbol{\cdot} A\). Thus \(A^{2}=a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}\). But if we recall that \[ |A|=\sqrt{a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}} \] we have \[ A^{2}=|A|^{2}. \]

(Note that this equation makes sense, since both sides are numbers. Note also that if \(A \neq(0,0, \ldots, 0), A^{2}>0\).)

Now let us try to express, in terms of the language we have developed, what is to be meant by saying that two vectors are perpendicular. Suppose that \(A\) and \(B\) of the diagram are perpendicular. In particular, this means that if we lay off a segment of length \(|B|\) to the left of their common initial point, the two line segments marked || are of equal length. But if we consider the broken line segment as a vector directed to the left, we observe that this vector is \(-B\), and that the two equal line segments, directed as indicated by the arrows, are \(A-B\) and \(A-(-B)=A+B\). Thus a necessary condition for perpendicularity is \(|A-B|=|A+B|\).

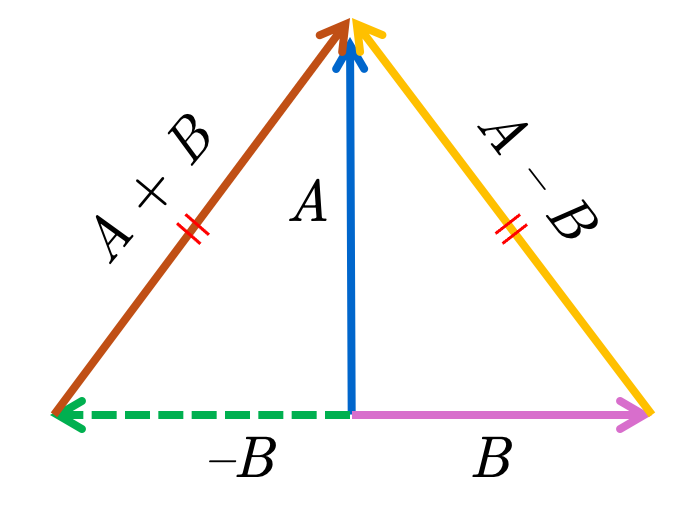
Conversely, if this is the case, then \(A\) is perpendicular to \(B\) in the sense of plane geometry. Squaring both sides of this equation and using the fact that \(A^{2}=|A|^{2}\) for any vector \(A\), we have \[ (A-B)^{2}=|A-B|^{2}=|A+B|^{2}=(A+B)^{2} \] Using the rules developed in the exercises, \[ (A-B)^{2}=A^{2}-2 A\boldsymbol{\cdot} B+B^{2},(A+B)^{2}=A^{2}+2 A\boldsymbol{\cdot} B+B^{2} \]

Thus \(A^{2}-2 A\boldsymbol{\cdot} B+B^{2}=A^{2}+2 A\boldsymbol{\cdot} B+B^{2}\), or

\[ -2 A \boldsymbol{\cdot} B=2 A \boldsymbol{\cdot} B, \quad \text { i.e., } \quad A\boldsymbol{\cdot} B=0 \]

Conversely, if \(A\boldsymbol{\cdot} B=0\), we see that \(|A-B|^{2}=|A+B|^{2}\). But since both \(|A-B|\) and \(|A+B|\) are non-negative, this means that \(|A-B|=|A+B|\), or that \(A\) and \(B\) are perpendicular.

Thus we may regard this result as our definition of perpendicularity in \(n\) dimensions:

Now suppose \(A\) and \(B\) are non-zero vectors (recalling that the zero vector is \((0,0, \ldots, 0)\) ). Then the quantity \[ |B| A-|A| B \] is a vector. Therefore the number \((|B| A-|A| B)^{2}\) is either positive or zero, and is zero only if \(|B| A-|A| B=0\) (vector), i.e., only if \[ |B| A=|A| B \] Now \[ \begin{aligned} (|B| A-|A| B)^{2} &=|B|^{2} A^{2}-2|A||B| A \boldsymbol{\cdot} B+|A|^{2} B^{2} \\ &=|B|^{2}|A|^{2}-2|A||B| A \boldsymbol{\cdot} B+|A|^{2}|B|^{2} \\ &=2|A||B|(|A||B|-A\boldsymbol{\cdot} B) \end{aligned} \] and this is \(\geq 0\). Since \(2|A||B|\) is positive, we can cancel it and get \(|A||B|-A B \geq 0\), or \[ A \boldsymbol{\cdot} B \leq|A||B| \] The two are equal only if \(|B| A=|A| B\), i.e., only if \(A\) and \(B\) have the same direction.

Likewise, \((|B| A+|A| B)^{2} \geq 0\), and is zero only if \(|B| A=-|A| B\), i.e., only if \(A\) and \(B\) have opposite directions. But \[ (|B| A+|A| B)^{2}=2|A||B|(|A||B|+A \boldsymbol{\cdot} B) \geq 0 \] giving \[ |A||B|+A \boldsymbol{\cdot} B \geq 0, \quad \text { or } \quad-|A||B| \leq A \boldsymbol{\cdot} B \]

Equality holds only if \(A\) and \(B\) have opposite directions. Combining the two results, we have in general \[ -|A||B| \leq A \boldsymbol{\cdot} B \leq|A||B| \] and we know exactly when one or the other of the inequalities becomes an equality. This result is known as Schwarz’s inequality.

Dividing the inequality through by \(|A||B|\) (which is positive), we have

\[ -1 \leq \frac{A \boldsymbol{\cdot} B}{|A||B|} \leq 1 \]

Therefore the number \(\dfrac{A \boldsymbol{\cdot} B}{|A||B|}\) can be the cosine of some angle. If we require that this angle \(\theta\) be between \(0^{\circ}\) and \(180^{\circ}\) (or in radians, between 0 and \(\pi\) ), then \(\theta\) is uniquely determined by giving \(\cos \theta\). Thus we define the angle between \(A\) and \(B\) to be that angle \(\theta\) between \(0^{\circ}\) and \(180^{\circ}\) such that \[ \cos \theta=\frac{A \boldsymbol{\cdot} B}{|A||B|}. \]

Observe that \(\theta=0^{\circ}\) if and only if \(A\) and \(B\) have the same direction, \(\theta=180^{\circ}\) if and only if they have opposite directions. So our terminology is consistent in this respect. Plane trigonometry will provide a more complete justification of our choice of definitions. Consider the triangle shown. The law of cosines tells us that \[ |A-B|^{2}=|A|^{2}+|B|^{2}-2|A||B| \cos \theta \]

Using what we know about vectors, this means that \[ (A-B)^{2}=A^{2}+B^{2}-2|A||B| \cos \theta \] or \[ \begin{gathered} A^{2}-2 A\boldsymbol{\cdot} B+B^{2} \\ =A^{2}+B^{2}-2|A||B| \cos \theta \end{gathered} \] i.e., \[ -2 A \boldsymbol{\cdot} B=-2|A||B| \cos \theta \] and finally \[ \bbox[5px,border:1px solid black;background-color:#f2f2f2]{A \boldsymbol{\cdot} B=|A||B| \cos \theta} \] which agrees with our definition of \(\theta\).