Points
In high school, one learns to think of a point as something which has no size but to which one can assign a definite location. But this concept is so idealized that we cannot realize it in nature. For certainly any dot we draw on the blackboard has dimensions, and the principles of modern physics tell us that the determination of a precise location for an object is impossible. Therefore, the things which we shall call points must come from an ideal world, and that will be the world of numbers.
Let us analyze for a moment the procedure of making a graph. For example, we might be measuring the temperature at various times, say hourly, on a certain day. Then we would describe our data graphically as shown:
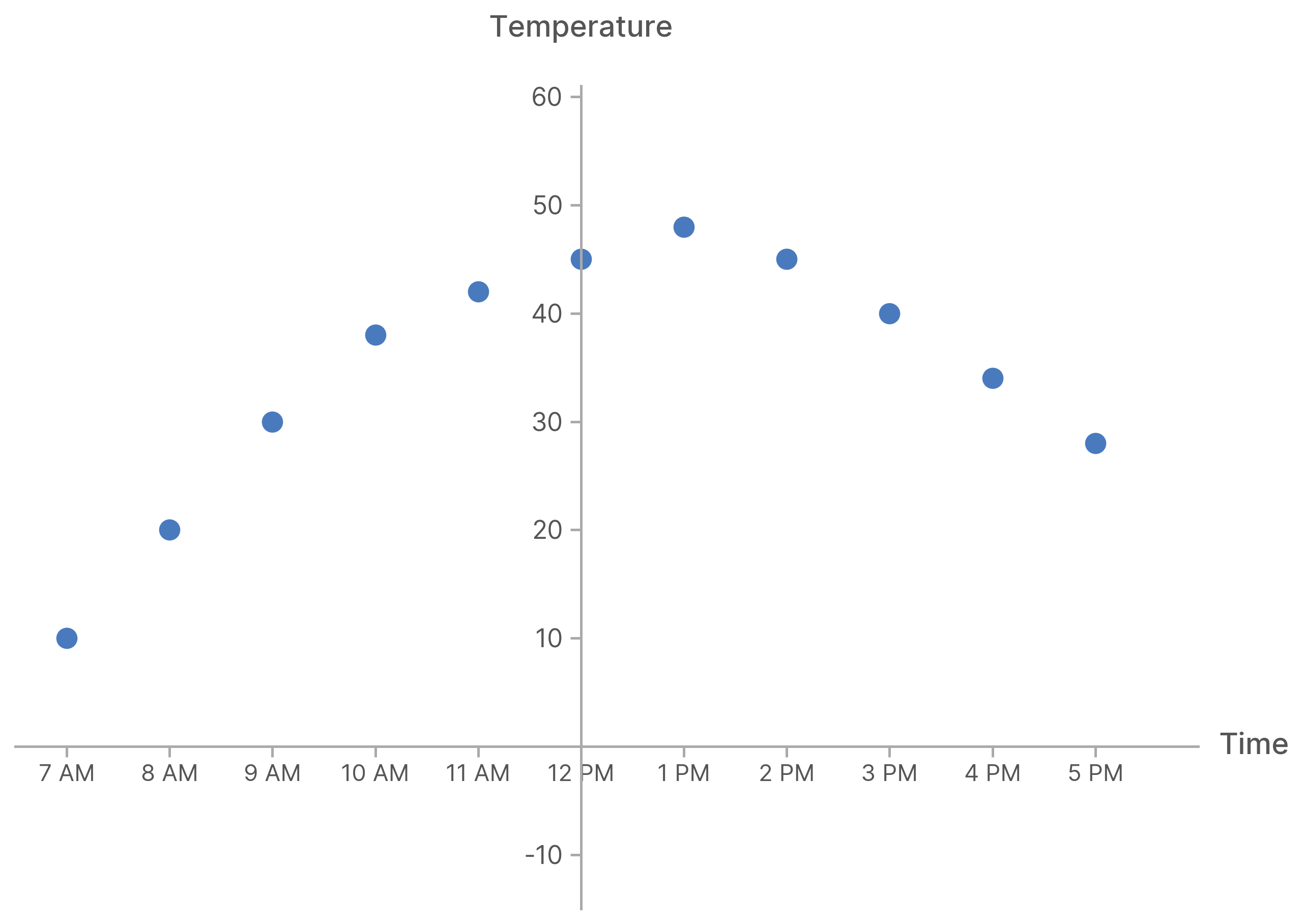
Each of the dots we have indicated, or each point of our graph, corresponds to a pair of numbers, e.g., (9 A.M., $30^{\circ}$ ). The first number indicates the (signed) distance from a fixed vertical line of reference; this point is -3 hours from the noon-line. Similarly the second number indicates the distance above the zero-degree line, in this case +30 degrees.
If we could extend indefinitely the range of available times and temperatures, it is evident that we could represent every point in the plane of the paper by a pair of numbers, and by only one such pair. For instance a point well off to the right and well below the zero-degree line might be represented by (noon two days later, $-379^{\circ}$ ), or simply (48, - 379). It is seen, then, that once a pair of reference lines (or axes) has been chosen, we can consider a point in the plane simply as a pair of numbers, representing its distances from the reference lines.
Likewise in space, we take three lines which intersect in a point. They then determine three planes, and we can identify every point in space with the triple of numbers consisting of its signed distances from these planes. Proceeding from this motivation, we define a point in n-dimensional space to be an n-tuple
$
\left(x_{1}, x_{2}, \ldots, x_{n}\right) \quad \text { of numbers. }
$
Then n-dimensional space is defined to be the totality, or set, of all n-tuples $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ of numbers.