Planes

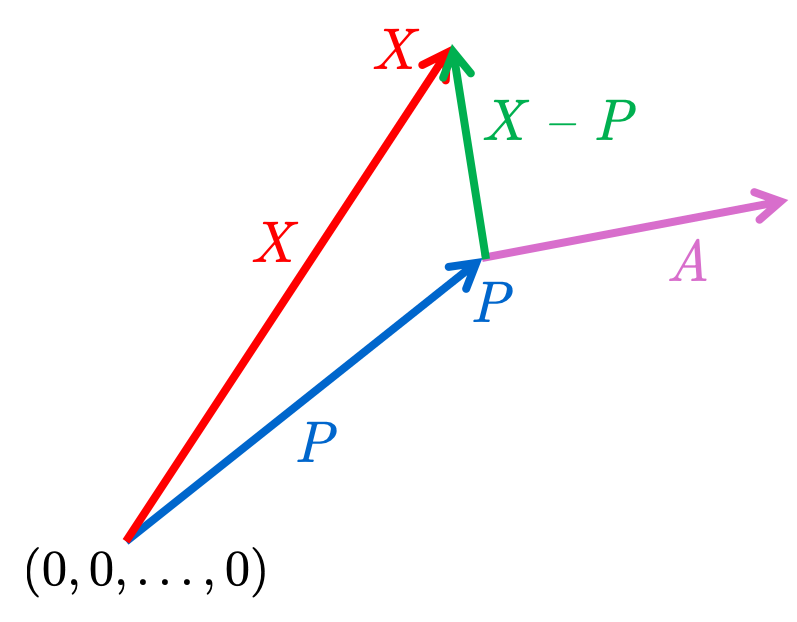
We shall next define another geometrical configuration in n-space; its category is again that of a set of points. It will be called a plane, and once again it is determined by giving a point and a vector. Our experience in geometry tells us that in ordinary 3-space a plane is completely determined if we know a point on the plane and a direction (i.e., a vector or a line segment) perpendicular to the plane. We shall find an equation which will provide a rule for deciding whether a given point is on our plane. For a given point \(P\) and a given vector \(A\), the set of points whose coordinates satisfy this equation will then be called the plane through \(P\) and perpendicular to \(A\).

Suppose \(X=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) is any point on such a plane. Then the line segment joining \(X\) and \(P\) must lie in this plane and therefore must itself be perpendicular to A. Considering this segment as a vector \(X-P\), as indicated in the diagram, we see that \((X-P)\boldsymbol{\cdot} A=0\), or that \[ \boxed{A\boldsymbol{\cdot} X=A \boldsymbol{\cdot} P} \] This is then the desired equation, and the plane is the set of all points \(X=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) satisfying this relation.

For example, the equation of a plane in 3-space would look like \[ 4 x-7 y+3 z=13 \] where we use \(X=(x, y, z)\) instead of \(\left(x_{1}, x_{2}, x_{3}\right)\). This is of the form \(A \boldsymbol{\cdot} X=A \boldsymbol{\cdot} P\), where \(A=(4,-7,3)\). The point \((1,0,3)\) is a point of the plane, which we could take as our P. We see from this how to recover a vector perpendicular to a plane from the equation: we simply form a vector whose components are the coefficients of \(x, y\) and \(z\), in this notation.

It is also evident how to determine from a pair of equations of this form whether the planes they define are parallel. For this question is equivalent to the question of parallelism for two vectors perpendicular to the planes. Since such vectors are given by reading off the coefficients of \(x, y\) and \(z\), we see that the two planes are parallel if and only if these coefficients are proportional.