Distance

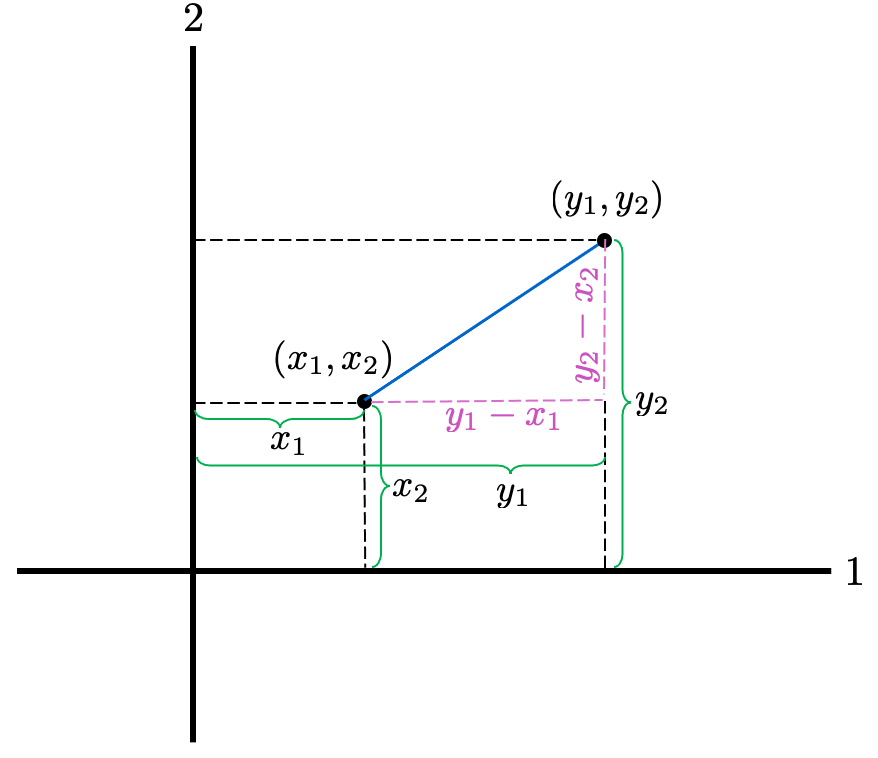
Now we return to two-dimensional space, where the notion of distance is a familiar one. In the figure below, $\left(x_{1}, x_{2}\right)$ and $\left(y_{1}, y_{2}\right)$ are two points in the plane, and the distance between them is the hypotenuse of the triangle with vertices
$
\left(x_{1}, x_{2}\right),\left(y_{1}, x_{2}\right) \text { and }\left(y_{1}, y_{2}\right)
$
or
$
\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}}
$
by the theorem of Pythagoras.

It is of some interest to give a very simple and often unfamiliar proof of the theorem of Pythagoras, as follows: We wish to prove that if $a$ and $b$ are the legs of a right triangle and $c$ is its hypotenuse, then $a^{2}+b^{2}=c^{2}$. Let us form a square of side $a+b$, and decompose it in two ways:

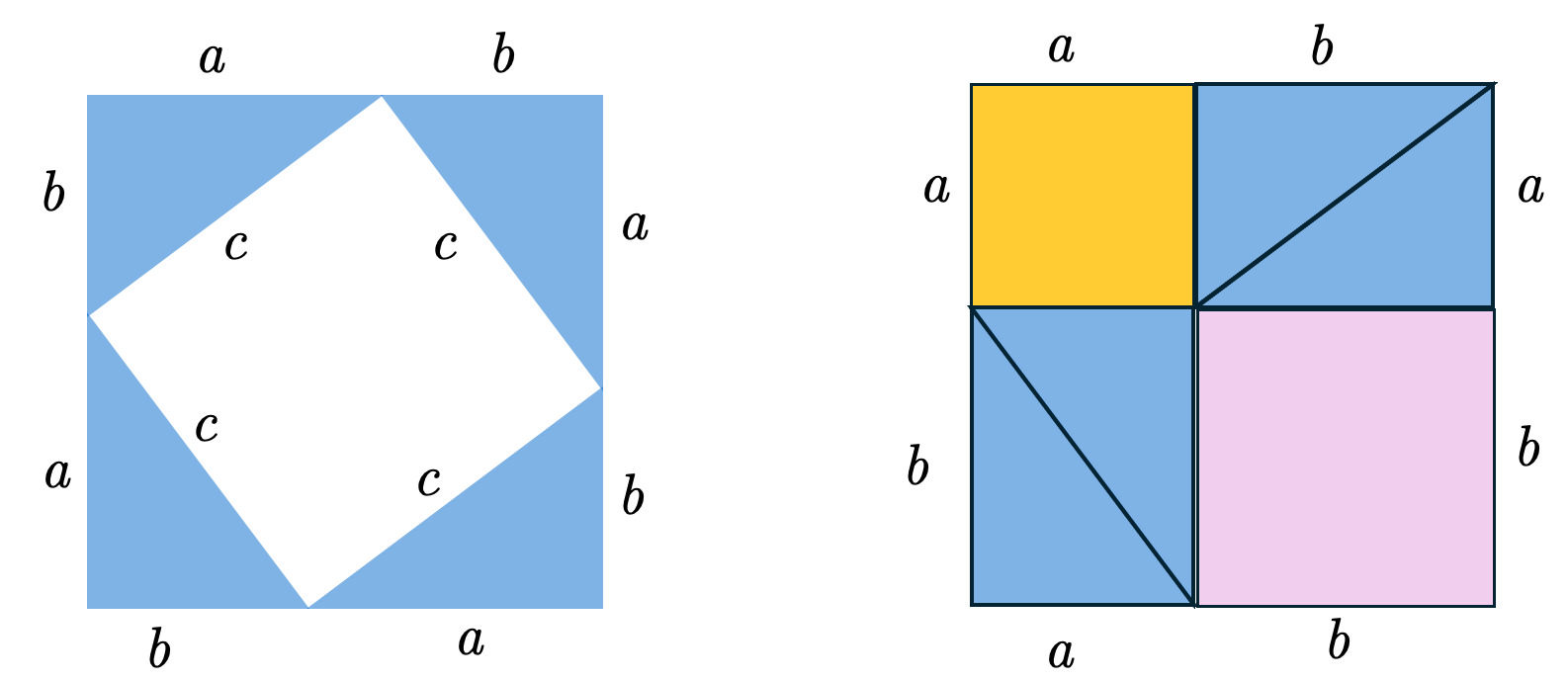
From (1), the area of the square is
$
c^{2}+4 \Delta
$
where $\Delta$ is the area of a right triangle with legs a and b. From (2), its area is
$
a^{2}+b^{2}+4 \Delta
$
Thus
$
a^{2}+b^{2}+4 \Delta=c^{2}+4 \Delta
$
or$
a^{2}+b^{2}=c^{2}
$
which was to be proved.

By applying the theorem of Pythagoras twice, we see that the distance between two points $\left(x_{1}, x_{2}, x_{3}\right)$ and $\left(y_{1}, y_{2}, y_{3}\right)$ in 3-space is
$
\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}+\left(y_{3}-x_{3}\right)^{2}}
$

Thus we are led to define the distance between two points $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ and $\left(y_{1}, y_{2}, \ldots, y_{n}\right)$ in n-space to be$
\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}+\ldots+\left(y_{n}-x_{n}\right)^{2}}
$

We observe that this is equal to
$
\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\ldots+\left(x_{n}-y_{n}\right)^{2}}
$

We also note that the distance between two points is 0 only if the points are not actually distinct, i.e., only if $x_{1}=y_{1}, x_{2}=y_{2}, \ldots, x_{n}=y_{n}$. (Why?)