Applications and Problems
We shall present a few applications of the technique of vectors to geometry, followed by some problems of more than routine interest. This list should be supplemented by a number of the problems to be found in any of the standard texts on analytic geometry of two and three dimensions.
Intersection of Two Planes in 3-Space
Consider the problem of finding the intersection of two planes in 3-space. In general, this will be a line; we can derive its equation from those of the planes in several ways:
- We could solve simultaneously the equations of the planes.
- We could find two points which are common to both planes, for instance by choosing two different fixed values for their third coordinates. We then obtain in each case a system of two linear equations in two unknowns (the first and second coordinates), which we solve. Then we find the connecting line.
- We could find one point \(P\) common to both planes, and then find a vector parallel to the line of intersection. The latter is accomplished by observing that any such vector \(A\) must be perpendicular to each of the known vectors \(B, C\) perpendicular to the individual planes. From the exercises on vector products, we see that we can take as our vector \(A\) the vector product \(B \times C\). The formula \(P+t A\) gives the line.
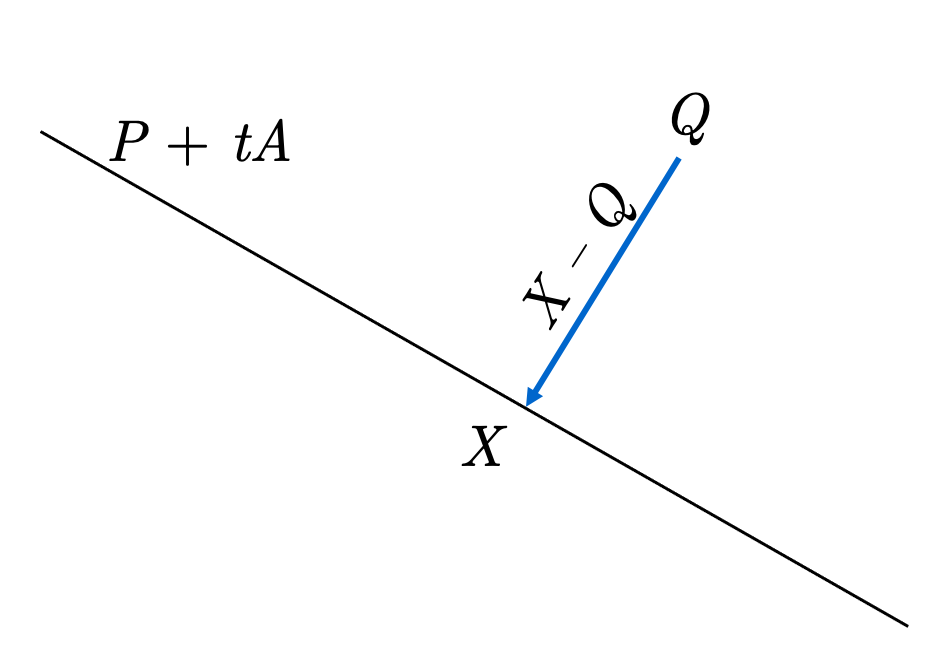
Distance from a Point to a Line in n-Space
Let \(P+t A\) be a line in n-space, \(Q\) a point not on the line; let us find the foot of the perpendicular from \(Q\) to this line.
If \(X\) is this point, then \(X=P+t_{0} A\) for some \(t_{0}\). Moreover, the segment connecting \(X\) with \(Q\), or the vector \(X-Q\), is to be perpendicular to the line \(P+t A\), therefore to the vector \(A\). Now \(X-Q=P+t_{0} A-Q\), giving \[ \left(P+t_{0} A-Q\right)\boldsymbol{\cdot} A=0 \]
This is a linear equation, which we solve for \(t_{0}\). The desired point is then found by substituting this value for \(t_{0}\) in \(X=P+t_{0} A\). The distance between \(Q\) and the line is simply \(|X-Q|\).
Distance Between Two Lines
Now let \(P+t A\) and \(Q+s B\) be two non-intersecting lines. Let \(X=P+t_{0} A\) and \(Y=Q+s_{0} B\) be the endpoints of their common perpendicular. Then \((X-Y)\boldsymbol{\cdot} A=0\) and \((X-Y)\boldsymbol{\cdot} B=0\). These give us two linear equations which we solve for \(s_{0}\) and \(t_{0}\). The resulting points \(X\) and \(Y\) determine the common perpendicular. The distance between the two lines is \(|X-Y|\).
Angle Between Two Planes
The angle between two planes is found by using the angle between two vectors, i.e., by reading off two vectors perpendicular to the planes from their equations and finding the angle between these vectors. Since two vectors having opposite directions determine the same plane, there are two possible answers, consisting of supplementary angles. We agree to take the angle between \(0^{\circ}\) and \(90^{\circ}\).
PROBLEMS
1. If a is a number, define its absolute value |a| by \(|a|=\sqrt{a^{2}}\). Show that \(|a A|=|a||A|\), where \(A\) is a vector.
2. If \(A\) and \(B\) are vectors, show that \((|A|+|B|)^{2}-(A+B)^{2} \geq 0\). Use this to prove the triangle inequality: \[ |A+B| \leqq|A|+|B|. \] When can this be an equality?
3. In n-space, let \(A_{1}=(1,0, \ldots, 0), A_{2}=(0,1,0, \ldots, 0), \ldots, A_{n}=(0, \ldots, 0,1)\). Show the following: a) If \(a_{1}, a_{2}, \ldots, a_{n}\) are numbers such that \(a_{1} A_{1}+a_{2} A_{2}+\ldots+a_{n} A_{n}=0\), then \(a_{1}=a_{2}=\ldots=a_{n}=0\). b) If \(B\) is any vector in n-space, there are numbers \(c_{1}, c_{2}, \ldots, c_{n}\) such that \(B=c_{1} A_{1}+c_{2} A_{2}+\ldots+c_{n} A_{n}\). How many such sets of numbers are there for a given \(B\) ? c) \(A_{1}^{2}=1\) and \(A_{1} A_{j}=0\) if \(1 \neq j\), for all 1 and \(j\). d) If \(B\) is any vector in n-space and \(B A_{1}=B A_{2}=\ldots=B A_{n}=0\), then \(B=0\). e) If \(A\) is any vector in n-space, and if \(A=a_{1} A_{1}+a_{2} A_{2}+\ldots+a_{n} A_{n}\), then \(|A|^{2}=a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}\) and each \(a_{1}=A A_{1}\).
4. Show by vectors that the diagonals of a rhombus are perpendicular.
5. Show that the medians of the triangle with vertices \(P, Q\), \(R\) meet in \(\frac{1}{2}(P+Q+R)\). (Observe that the midpoint of the side \(\overline{P Q}\) is \(\frac{1}{2}(P+Q)\).
6. What is the plane through \((-1,2,-3)\) such that any vector perpendicular to the plane forms equal angles with the vectors \((1,0,0),(0,1,0)\) and \((0,0,1)\) ?
7. Show that the planes \(x-y+2 z=4\) and \(2 y-2 x-4 z+7=0\) are parallel. Find the distance between them.
8. Let \(A\) and \(B\) be non-zero vectors in 3-space. Prove that \(A\) and \(B\) are parallel if and only if \(A \times B=0\).
9. Prove the law of sines using vectors in 3-space.
10. What is the set of points \(X\) in 3-space such that the vector from \(X\) to \((1,3,5)\) is perpendicular to the vector from \((-5,-1,3)\) to \(X\) ? Show that this is the equation of a sphere with center \((-2,1,4)\) and radius \(\sqrt{ } 14\).
11. Let \(B\) and \(W\) be vectors, different from 0 . Show that there exist vectors \(B_{1}\) and \(B_{2}\) such that
- \(B_{1}\) is parallel to \(W\),
- \(B_{2}\) is perpendicular to \(W\),
- \(B_{1} \cdot B_{2}=0\), and
- \(B=B_{1}+B_{2}\) Show that \(B_{1}\) and \(B_{2}\) are unique.
12. Let \(R\) and \(S\) be the points \((1,2,3,4)\) and \((4,3,2,1)\); let \(A\) be the vector \((1,1,1,1)\); let \(M\) be the line through \(R\) parallel to \(A\); and notice that \(S\) does not lie on \(M\).
- Given a point \(Q\) on \(M\), compute the distance between \(S\) and \(Q\) and show that it is \(\geq 2 \sqrt{5}\).
- Show that the distance between \(S\) and \(Q\) is precisely \(2 \sqrt{5}\) for just one \(Q_{0}\), being actually \(>2 \sqrt{5}\) for all other points \(Q\). Compute the coordinates of this \(Q_{0}\).
- Show that the vector \(S-Q_{0}\) is perpendicular to the vector A.
13. Keeping the results of (2) in mind, consider (in n-space) a point \(R\) and a vector \(A\) whose length \(|A|\) is \(>0\); let \(M\) be the line through \(R\) parallel to \(A\); and let \(S\) be a point not on \(M\).
- Show that there is just one point \(Q_{0}\) on \(M\) such that the vector \(S-Q_{0}\) is perpendicular to \(A\) and compute its coordinates.
- Given a point \(Q\) on \(M\), compute the distance from \(S\) to \(Q\) and show that it is \(\geq\left|S-Q_{0}\right|\). Show that the distance from \(S\) to \(Q\) is precisely \(\left|S-Q_{0}\right|\) if and only if \(Q=Q_{0}\).
14. Compute (in 3-space) the equation of the plane which passes through the points \((1,0,0),(0,1,0)\), and \((0,0,1)\).
- Compute the distance \(|S-Q|\) between the point \(S=(2,2,2)\) and a point \(Q\) in this plane.
- Compute the minimum distance and call it \(\Delta\).
- Show that there is just one point \(Q_{0}\) in the plane such that the distance \(\left|S-Q_{0}\right|=\Delta\). Compute the coordinates of \(Q_{0}\).
- Show that the vector \(S-Q_{0}\) is perpendicular to the plane.
Given three vectors \(A, B\), and \(C\) (in n-space) show that the relation \((A \cdot B) C=A(B \cdot C)\) is not, in general, true.
A cube in n-dimensional space is a set of points ( \(x_{1}, \ldots\), \(x_{n}\) ) satisfying \[ a_{1} \leqq x_{1} \leqq a_{1}+d, a_{2} \leqq x_{2} \leqq a_{2}+d, \ldots, a_{n} \leqq x_{n} \leqq a_{n}+d, \] for some set of \(n\) numbers \(a_{1}, \ldots, a_{n}\) and some \(d>0\). Then the vertices of the cube are the points of the form \(\left(b_{1}, \ldots, b_{n}\right)\), where each \(b_{i}\) is either \(a_{i}\) or \(a_{i}+d\). An edge of the cube is a line segment joining two vertices \(\left(b_{1}, \ldots, b_{n}\right)\) and \(\left(c_{1}, \ldots, c_{n}\right)\), where \(b_{i}=c_{i}\) for all except one of the \(i\)’s.
How many vertices and edges has a cube in 2-space? in 3-space? in 4-space? in n-space? How would you define a 2-dimensional face of an n-dimensional cube ( \(n \geq 2\) )? a k-dimensional face ( \(n \geq k\) )? How many of these are there?