Series
A. Power Series
Problem: Prove \[ 1+x+x^2+x^3+\cdots = \dfrac{1}{1-x} \]
Hint
Recall the sum of a geometric sequence (progression): \[ a+aq+aq^2+\cdots+aq^{n-1}=\frac{a(1-q^n)}{1-q} \]
Problem: Sum \[ 1+a\cos\theta + a^2\cos 2\theta + a^3\cos 3\theta + \cdots \]
Hint
Notice that \((e^{i\theta})^n=\cos n\theta + i \sin n\theta\).
B. Summation by Integration and Differentiation
Consider the following series \[ 1(x) - \dfrac{1}{2}(x^2) + \dfrac{1}{3}(x^3) - \dfrac{1}{4}(x^4) + \cdots = S(x) \]
Explanation
This line defines an infinite series as a function, which we’ll call S(x). This type of series, which involves powers of x, is known as a power series. The goal is to find a more common function (like sin(x) or ln(x)) that is equal to this infinite sum.
\[ 1 - x + x^2 - x^3 + x^4 + \dots = S'(x) \]
Explanation
Here, you’ve taken the derivative of the series S(x) term by term.
- The derivative of x is 1.
- The derivative of -(1/2)x² is -x.
- The derivative of (1/3)x³ is x².
Taking the derivative often simplifies a series into a more recognizable pattern. The result is labeled S’(x), the derivative of S(x).
\[ S'(x) = \dfrac{1}{1+x} \]
Explanation
This step recognizes that the new series (1 - x + x² - …) is a well-known pattern called a geometric series. The formula for a geometric series is a / (1 - r), where a is the first term and r is the common ratio. In this case, the first term a=1 and the ratio r = -x. Plugging this into the formula gives 1 / (1 - (-x)), which simplifies to 1 / (1+x).
\[ S(x) = \ln(1+x)+C \]
Explanation
To get back to the original function S(x) from its derivative S’(x), you need to do the opposite of differentiating: integrating. The integral of 1 / (1+x) is ln(1+x). Whenever you find an indefinite integral, you must add a constant of integration, written as + C, because the derivative of any constant is zero.
evaluate constant for \(x=0\) \[ S(0) = \ln 1 + C \] \[ 0=0+C \]
Explanation
- On the right side, we know that ln(1) = 0.
- On the left side, we plug x=0 into the very first line of our notes: S(0) = 1(0) - (1/2)(0)² + …. Every term becomes zero, so S(0) = 0.
This gives us the simple equation 0 = 0 + C, which means C must be 0.
\[ S(1) = \ln 2 = .69315 \]
[From calculus, recall the following theorem: ]
Convergence: Ratio Test If the \(\lim_{n\to\infty} x_{n+1}/x_n < 1\) the series converges.
C. Abel Summability.
Consider the series \[ 1-2+3-\cdots \] Convert it into a power series in x as follows: \[ S(x) = 1-2x+3x^2-\cdots \] Sum this power series: \[ \int S(x)dx = x-x^2+x^3-\dots = \dfrac{x}{1+x} \] \[ S(x) = \dfrac{d}{dx}\left(\dfrac{x}{1+x}\right) = \dfrac{1}{(1+x)^2} \] The Abel sum of the original series is defined as the \(\lim_{x\to 1} S(x)\) \[ \text{Abel sum} = \lim_{x\to 1} \left[\dfrac{1}{(1+x)^2}\right] = \dfrac{1}{4} \] In general, oscillating series can be summed, but the order of the terms must not be changed.
Explanation
While the series \(1 - 2 + 3 - \dots\) is divergent in the usual sense, it is Abel summable to \(\frac{1}{4}\). This is a different notion of convergence based on taking a limit of a related power series as \(x \to 1^-\). For more details, see Abel summability.
D. Summation of Series by Integration and Differentiation.
\[ S = 1+\dfrac{1}{4}+\dfrac{1}{9}+\dfrac{1}{16}+\cdots \]
Explanation
This is the infinite series we want to understand or potentially find a sum for. It’s the sum of the reciprocals of perfect squares, which can be written as \(\sum_{n=1}^{\infty} \frac{1}{n^2}\). This specific series is known as the Basel Problem, and its sum is famously \(\frac{\pi^2}{6}\).
\[ S(x) = x+x^2/4+x^3/9+\cdots \]
Explanation
To use calculus, we convert the sum into a power series function, \(S(x)\). Notice that if you substitute \(x=1\) into this function, you get the original series \(S\). So, the goal is to find a closed-form expression for \(S(x)\) and then evaluate it at \(x=1\). This particular power series can be written as \(\sum_{n=1}^{\infty} \frac{x^n}{n^2}\).
\[ S'(x) = 1+x/2+x^2/3+\cdots \]
Explanation
Here, you’ve taken the derivative of \(S(x)\) term by term.
\[ S'(x)= -\dfrac{\ln(1-x)}{x} \]
Explanation
This is the crucial step where you recognize the simplified series as a known function. The series \(1 + \frac{x}{2} + \frac{x^2}{3} + \dots\) is exactly the expansion of \(-\frac{\ln(1-x)}{x}\).
(This comes from the Taylor series expansion of \(\ln(1-x) = -x - \frac{x^2}{2} - \frac{x^3}{3} - \dots\), and then dividing by \(x\). For the expansion of \(\ln(1-x)\) see below.)
\[ S(x) = -\int\dfrac{\ln(1-x)}{x}dx \]
Explanation
To get back to the original function \(S(x)\) from its derivative \(S'(x)\), you perform the antidifferentiation (integration). So, \(S(x)\) is the indefinite integral of the expression you found for \(S'(x)\).
One should know and recognize the series for the following expressions: (1) \[\dfrac{1}{1-x} = 1+x+x^2+x^3+\cdots\] (2) \[-\ln(1-x) = x+\dfrac{x^2}{2}+\dfrac{x^3}{3}+\cdots\] (3) \[\tan^{-1}x = x-\dfrac{x^3}{3}+\dfrac{x^5}{5}-\dfrac{x^7}{7}+\cdots\] (4) \[e^x = 1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots\] (5) \[\sin x = x-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\cdots\] (6) \[\cos x = 1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\cdots\] (7) \[\dfrac{1}{(1+x)^2} = 1-2x+3x^2-\cdots\] (8) \[\dfrac{1}{(1+x)^{1/2}} = 1-\dfrac{1}{2}x+\dfrac{3}{8}x^2-\dfrac{5}{16}x^3+\cdots\] A useful relation \(e^{i\theta} = \cos\theta + i\sin\theta\)
Problem: Sum: \[ \dfrac{1}{2!} + \dfrac{2}{3!} + \dfrac{3}{4!} + \cdots \] \[ \dfrac{1}{1\cdot 2} + \dfrac{1}{2\cdot 3} + \dfrac{1}{3\cdot 4} + \dots \]
E. Summation of Series by Adding Terms.
Consider the series \[ 1+\dfrac{1}{4}+\dfrac{1}{9}+\cdots \] We can sum it as follows: 1.000+ .250 +.111 + .0625 + …
By taking enough terms we can obtain any desired accuracy. If the series is slow to converge it is sometimes possible to replace the higher terms by an integral:
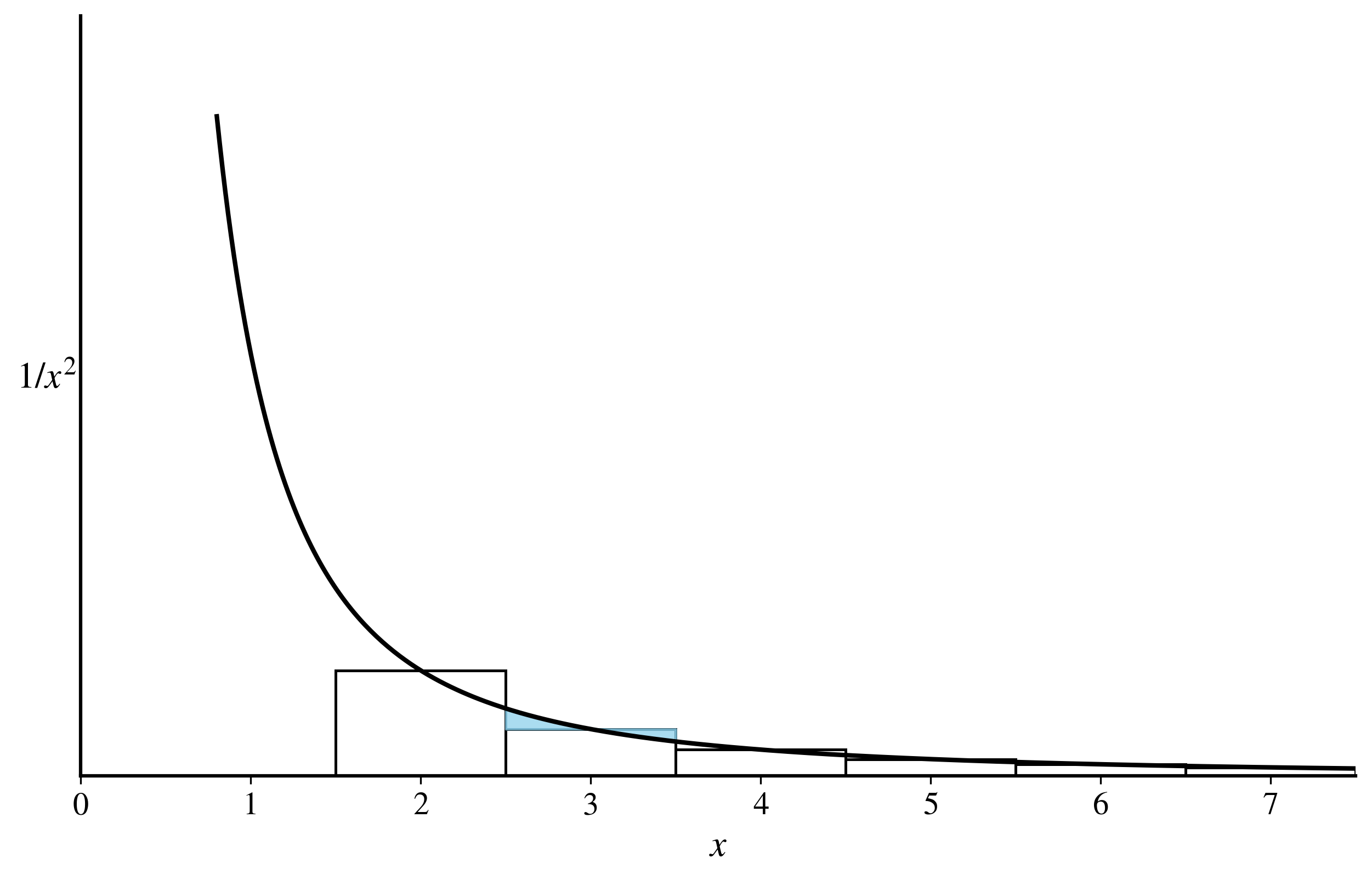
Examination of the above diagram shows that \[ \dfrac{1}{3^2}+\dfrac{1}{4^2}+\dots \approx \int_{2.5}^\infty \dfrac{dx}{x^2} \] \[ \approx \dfrac{1}{2.5} = .4 \] The sum of our series is then 1.000+ .250 + .400 = 1.650
Explanation
Here we are trying to find the sum of the series: \[ S = 1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \dots = \sum_{n=1}^{\infty} \frac{1}{n^2} \]
There are two methods to find this sum:
- Direct Summation: The first method is to simply start adding the terms one by one (
1.000 + 0.250 + 0.111 + ...). We note that for a “slow to converge” series, this is inefficient. You would have to add thousands of terms to get an accurate answer. - Integral Approximation: The second, more clever method is to add the first few terms directly and then approximate the rest of the sum (the “tail” of the series) with an integral. This works because the sum of the series can be visualized as the area of a set of rectangles, which can be closely approximated by the area under a smooth curve.
** Why the Integral Starts at 2.5 (Using the Diagram)**
The core of the technique is approximating the sum of the “higher terms” with an integral. In this example, the author decides to calculate the first two terms exactly and approximate the rest:
\[ S = \underbrace{1 + \frac{1}{4}}_{\text{Calculated Exactly}} + \underbrace{\left( \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + \dots \right)}_{\text{To be Approximated}} \]
This “tail” of the series can be written as: \[ \text{Tail} = \sum_{n=3}^{\infty} \frac{1}{n^2} \]
Now, let’s look at the diagram to understand the approximation for this tail.
- The Rectangles Represent the Sum: The diagram shows the function
y = 1/x². The rectangles represent the terms of the series.- The rectangle at
x=3has a width of 1 and a height of1/3² = 1/9. Its area is 1/9. - The rectangle at
x=4has a width of 1 and a height of1/4² = 1/16. Its area is 1/16. - Therefore, the sum of the tail,
1/9 + 1/16 + ..., is equal to the total area of all the rectangles starting from x=3.
- The rectangle at
- The Integral Represents the Area Under the Curve: The integral
∫(1/x²) dxcalculates the area under the smooth curvey = 1/x². Finding the Best Approximation: We want to find an integral whose area is very close to the area of the rectangles from
x=3onwards.- If we started the integral at
x=3(i.e.,∫ from 3 to ∞), the curve would run under the top of the rectangles. This would give us an underestimate of the true sum. - If we started the integral at
x=2(i.e.,∫ from 2 to ∞), the curve would run above the top of the rectangles. This would give us an overestimate.
So we choose
x = 2.5as the starting point. This is a very clever choice based on the midpoint rule of approximation.By starting the integral at 2.5, you are assuming that the area of the rectangle at
x=3is best approximated by the area under the curve on the interval[2.5, 3.5].As you can see in this enhanced diagram, the small bit of area the integral misses on the left side of the rectangle (the white region with red outline) is almost perfectly canceled out by the extra area the integral includes on the right side (the shaded region).
This logic extends to all the other terms. The area of the rectangle at
x=4is approximated by the integral from3.5to4.5, and so on. Therefore, the entire sum of the tail is approximated by the integral starting from2.5: \[ \sum_{n=3}^{\infty} \frac{1}{n^2} \approx \int_{2.5}^{\infty} \frac{1}{x^2} dx \]- If we started the integral at
** The Final Calculation**
The notes complete the process:
- Calculate the integral: \[ \int_{2.5}^{\infty} \frac{1}{x^2} dx = \left[ -\frac{1}{x} \right]_{2.5}^{\infty} = \left( -\frac{1}{\infty} \right) - \left( -\frac{1}{2.5} \right) = 0 + \frac{1}{2.5} = 0.4 \]
- Add the parts together: \[ S \approx 1 + 0.250 + 0.400 = 1.650 \]
This is an excellent approximation. The true sum of this series (the Basel Problem) is known to be π²/6 ≈ 1.6449, so this simple method is remarkably accurate.
Since the error will be principally in the first terms some idea of its magnitude may be gotten by looking at the next best approximation: \[ \dfrac{1}{4^2}+\dfrac{1}{5^2}+\cdots \approx \int_{3.5}^\infty \dfrac{dx}{x^2} \] \[ \approx .286 \] The new sum is: 1.000+ .250 + .111 + .286 = 1.647 we see that we have made an error of only .003. We can guess from this that the third figure is probably about 6.