Equations
The simplest way to solve any equation - except linear or quadratic equations - is by trial and error.
A. Interpolation
To solve \[ \dfrac{1}{1+x^2} = 2x \]
Let:
| x | LHS | RHS | DIFF | |
|---|---|---|---|---|
| 0 | 1 | 0 | 1 | } 2.5 |
| 1 | .5 | 2 | -1.5 | |
| .4 | .862 | .8 | .062 | |
| .5 | …. | …. | …. |
Explanation
This document explains how to solve the equation \(1 / (1 + x²) = 2x\) using a numerical method of trial and error, often called interpolation. To find the solution, we create a table to compare the Left-Hand Side (LHS) and Right-Hand Side (RHS) of the equation, aiming to find a value of \(x\) where their difference (DIFF) is zero. We first test x=0, which gives a difference of +1, and then x=1, which gives a difference of -1.5. Since the sign of the difference changes between these two points, we know the solution must lie between 0 and 1. Because the absolute difference for x=0 (which is 1) is less than the difference for x=1 (which is 1.5), we can guess that the solution is closer to x=0, prompting our third guess of x=0.4. This trial yields a very small positive difference of +0.062. With a positive difference at x=0.4 and a negative one at x=1, we conclude that the solution is between 0.4 and 1. However, since the difference for x=0.4 is very small, we guess the solution is much closer to 0.4, so our fourth guess is x=0.5 to further narrow the interval and pinpoint the exact answer.
B. Iteration
Solve the equation for \(x\): \[ x = \dfrac{1}{2}\left(\dfrac{1}{1+x^2}\right) \]
| trial \(x\) | result \(x\) |
|---|---|
| 0 | \(\to .5\) |
| .5 | \(\to .4\) |
| .4 | \(\to .431\) |
| … | … |
Explanation
This example demonstrates another powerful numerical technique, known as Fixed-Point Iteration, to solve an equation. Notice that, this is the same equation as in the previous example (1 / (1 + x²) = 2x), just rearranged to isolate x on one side: \[ x = \frac{1}{2}\frac{1}{1+x^2} \] The core idea of this method is to find a value for x (a “fixed point”) that remains unchanged when we plug it into the expression on the right. We do this by starting with an initial guess and then iteratively feeding the result back into the equation until the numbers stop changing significantly.
Here is a step-by-step breakdown of the process shown:
- Initial Guess (Trial 1): We start with an initial guess of
trial x = 0. We plug this into the right side of the equation:- Result =
1/2 * (1 / (1 + 0²)) = 1/2 * (1) = 0.5This result,0.5, becomes our next trial value.
- Result =
- First Iteration (Trial 2): Now, we use this result as our new
trial x = 0.5:- Result =
1/2 * (1 / (1 + 0.5²)) = 1/2 * (1 / 1.25) = 0.5 * 0.8 = 0.4
- Result =
- Second Iteration (Trial 3): We repeat the process with
trial x = 0.4:- Result =
1/2 * (1 / (1 + 0.4²)) = 1/2 * (1 / 1.16) ≈ 0.5 * 0.862 = 0.431
- Result =
The process continues this way. We would next use 0.431 as our trial x and calculate a new result. With each step, the “trial x” and “result x” get closer to each other. The solution is found when the value we put in is the same as the value that comes out (i.e., when the sequence converges).
If the equation is solved in the form \(x = \sqrt{\dfrac{1}{2x}-1}\), however, the results diverge. If the results do diverge solving the equation in the inverse manner will make them converge.
C. Newton’s Method
Solve the equation in the form \(f(x)=0\). Let \(x_1\) be the first trial, then the second trial is given by the relation \[ x_2 = x_1 - \dfrac{f(x_1)}{f'(x_1)} \] This procedure is equivalent to extrapolating back along the tangent. If the curve is full of wiggles things may diverge.
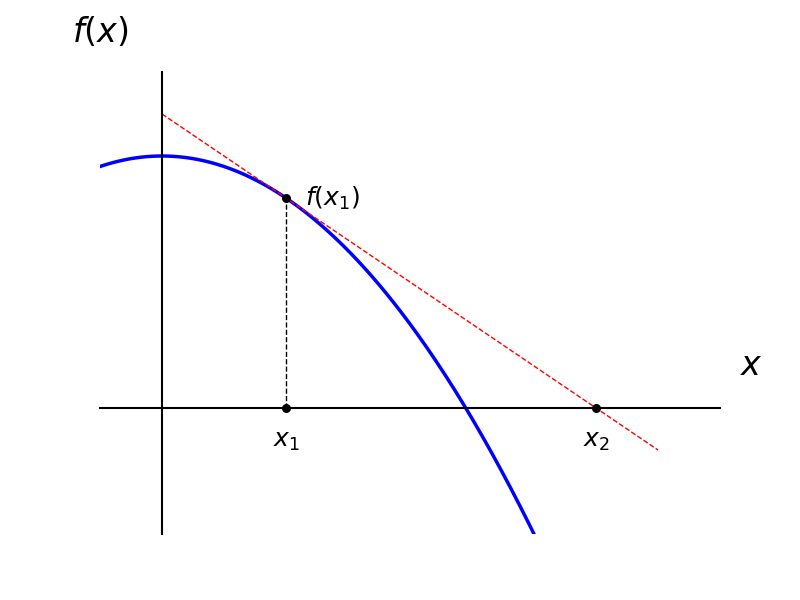
[Let’s go back to the previous example]
\[ f(x) = \dfrac{1}{1+x^2} - 2x = 0 \] \[ f'(x) = \dfrac{-2x}{(1+x^2)^2} - 2 \]
| x | f(x) | f’(x) |
|---|---|---|
| 0 | 1 | -2 |
| .5 | .2 | …. |
| … | …. | …. |
Explanation
The table shows the step-by-step process of applying the method.
- First Guess: You start with a simple initial guess: x₁ = 0.
- Plug in the Guess: At x=0, you calculate the values of the function and its derivative:
- f(0) = 1/(1+0²) - 2(0) = 1
- f’(0) = -2(0)/(1+0²)² - 2 = -2
- Calculate the Next Guess (x₂): Now, you use the Newton’s Method formula: \[x_2=x_1-\frac{f(x_1)}{f'(x_1)}=0-\frac{1}{-2}=0.5\]
- The Next Step (Row 2): Your new, improved guess is x₂ = 0.5. The second row of the table would use this value to calculate f(0.5) and f’(0.5) in order to find an even better guess, x₃. This process continues until f(x) is extremely close to zero.
Problem: Find first positive root of \(e^{-x} = \cos x\) by all three methods to 2 decimals. Estimate higher roots.