To multiply two polynomials, apply the distributive property by multiplying each term of the first polynomial by each term of the second. Then use the exponent rule \[ax^{n}\cdot bx^{m}=ab\ x^{m+n},\] add the resulting products and collect any like terms.
The Product of Two Monomials
To multiply two monomials, multiply the coefficients and add the exponents. For example: \[(-4y^3)(5y^6) = -20y^{9}.\] The Product of a Monomial and a Polynomial
Use the distributive property to multiply a monomial by each term of a polynomial. For example: \[3x^2(2x^3 - 4x + 5) = 6x^5 - 12x^3 + 15x^2.\]
Multiplying Two Polynomials
When multiplying two polynomials, distribute each term of the first polynomial across all terms of the second. For example: \[(3x - 2)(2x^2 - 3x + 4).\] Distribute \(3x\) across the trinomial: \[3x(2x^2 - 3x + 4) = 6x^3 - 9x^2 + 12x.\] Distribute \(-2\) across the trinomial: \[-2(2x^2 - 3x + 4) = -4x^2 + 6x - 8.\] Combine like terms: \[6x^3 - 13x^2 + 18x - 8.\]
Example 1.9 . Multiply: \((4x^{2}-3x+5)(2x^{3}-x)\)
Solution
\[\begin{align} (4x^{2}-3x+5)(2x^{3}-x) & =4x^{2}(2x^{3}-x)-3x(2x^{3}-x)+5(2x^{3}-x)\\ & =8x^{5}-4x^{3}-6x^{4}+3x^{2}+10x^{3}-5x\\ & =8x^{5}-6x^{4}+(10-4)x^{3}+3x^{2}-5x\\ & =8x^{5}-6x^{4}+6x^{3}+3x^{2}-5x \end{align}\]
It is clear that if \(A\) is a polynomial of degree \(n\) and \(B\) is a polynomial of degree \(m\) , then the product \(A\cdot B\) is a polynomial of degree \(n+m\) .
\[\text{deg}(A\cdot B)=\text{deg}(A)+\text{deg}(B)\]
In the above example, the first one is a polynomial of degree 2 and the second one is a polynomial of degree 3, and the product is a polynomial of \(5=2+3\) .
Table of Contents
Long Multiplication
When dealing with polynomials that have three or more terms, using a structured approach similar to long multiplication for numbers is often simpler and more reliable. Here is how to proceed:
- Select a Polynomial : Start with one of the polynomials (preferably the longer one) as your main reference.
- Multiply by Each Term :
- Multiply the first term of the second polynomial by every term in the first polynomial, and write the results in a row.
- Move to the second term of the second polynomial, repeat the process, and write the new results directly beneath the first row, aligning terms by their degree.
- Repeat for All Terms : Continue this process for all terms in the second polynomial.
- Add the Results : Once all the rows are written, add them together by combining like terms.
Key Tip : Keeping your work neatly aligned in columns based on the degree of the terms makes it easier to combine like terms and reduces mistakes.
Example 1.10 . Multiply \(2x^3-x^2+5\) by \(x-3+x^2\) .
Solution
We arrange the given polynomials in descending (or ascending) powers of \(x\) and place the multiplier under multiplicand.
We then write in separate rows the "partial products" corresponding to the several terms of the multiplier, placing them so that like terms, that is, terms of the same degree, are in the same column.
\[\begin{align} \phantom{2x^5-3x^4-3x^3+}2x^3-x^2+\phantom{x}+5&\\\times \phantom{2x^5-3x^4-3x^3-2x^2}(x^2+x-3)&\\[-6pt] \rule{5cm}{0.4pt}\\ -6x^3-3x^2\phantom{+3x}-15& &&{\color{blue}\leftarrow -3(2x^3-x^2+5)}\\ \phantom{-}2x^4-\phantom{2}x^3+\phantom{2x^2}+5x\phantom{+15}& &&{\color{blue}\leftarrow x(2x^3-x^2+5)}\\ 2x^5-\phantom{2}x^4~\phantom{-6x^3}+5x^2\phantom{+5x-15}& &&{\color{blue}\leftarrow x^2(2x^3-x^2+5)}\\ \end{align}\]
Finally, add these like terms by columns: \[\begin{align} \phantom{2x^5-3x^4-3x^3+}2x^3-x^2+\phantom{x}+5&\\\times \phantom{2x^5-3x^4-3x^3-2x^2}(x^2+x-3)&\\[-6pt] \rule{5cm}{0.4pt}\\[-2pt] -6x^3-3x^2\phantom{+3x}-15& &&{\color{blue}\leftarrow -3(2x^3-x^2+5)}\\ \phantom{-}2x^4-\phantom{2}x^3+\phantom{2x^2}+5x\phantom{+15}& &&{\color{blue}\leftarrow x(2x^3-x^2+5)}\\ 2x^5-\phantom{2}x^4~\phantom{-6x^3}+5x^2\phantom{+5x-15}& &&{\color{blue}\leftarrow x^2(2x^3-x^2+5)}\\[-6pt] \rule{5cm}{0.4pt}\\ 2x^5-3x^4-7x^3+2x^2+5x-15& &&{\color{blue}\leftarrow \text{combine like terms}} \end{align}\]
Therefore,
\[(2x^3-x^2+5)(x-3+x^2)=2x^5-3x^4-7x^3+2x^2+5x-15.\]
Example 1.11 . Multiply \((4x^2-3x+5)\) by \((2x^3-x)\) .
Solution
\[\begin{align} & &4x^2&-3x&+5\\ \times\qquad &(2x^3&&-x)\\ \hline &-4x^3&-3x^2&-15x\\ -8x^5-6x^4&-5x^3\\ \hline -8x^5-6x^4&-9x &-3x^2&-15x \end{align}\]
Therefore, \[(4x^2-3x+5)(2x^3-x)=-8x^5-6x^4-9x-3x^2-15x,\] as before .
FOIL Method for Multiplying Binomials
When multiplying two binomials, we can use a helpful mnemonic device called FOIL to remember the distributive property. FOIL stands for F irst, O uter, I nner, L ast. It outlines the steps to ensure we multiply each term in the first binomial by each term in the second binomial.
Let’s consider two binomials: \((a + b)\) and \((c + d)\) . To multiply them using the FOIL method, we follow these steps:
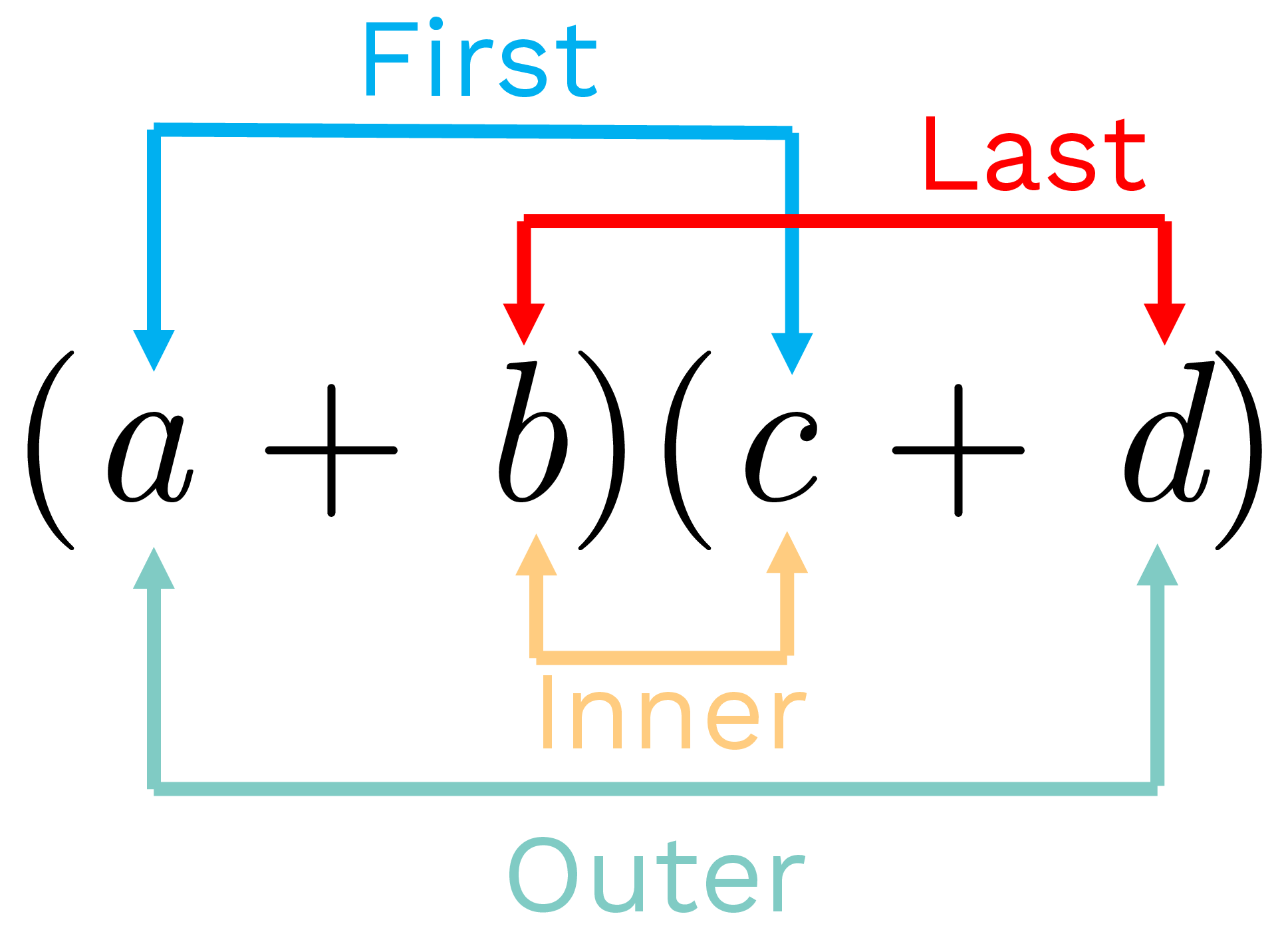
- F (First): Multiply the first terms of each binomial: \(a \times c = ac\) .
- O (Outer): Multiply the outer terms of the binomials: \(a \times d = ad\) .
- I (Inner): Multiply the inner terms of the binomials: \(b \times c = bc\) .
- L (Last): Multiply the last terms of each binomial: \(b \times d = bd\) .
Finally, we add the results of these four multiplications: \(ac + ad + bc + bd\) . So, \((a + b)(c + d) = ac + ad + bc + bd\) .
Example 1.12 . Multiply \((x + 2)(x - 3)\) using the FOIL method.
Solution
- F: \(x \times x = x^2\)
- O: \(x \times (-3) = -3x\)
- I: \(2 \times x = 2x\)
- L: \(2 \times (-3) = -6\)
Adding these terms together, we get: \(x^2 - 3x + 2x - 6\) .
Simplifying by combining like terms, we have: \[x^2 - x - 6.\]
Example 1.13 . Multiply \((2y - 5)(3y + 1)\) using the FOIL method.
Solution
- F: \((2y) \times (3y) = 6y^2\)
- O: \((2y) \times 1 = 2y\)
- I: \((-5) \times (3y) = -15y\)
- L: \((-5) \times 1 = -5\)
Adding these terms together: \(6y^2 + 2y - 15y - 5\) .
Simplifying by combining like terms: \[6y^2 - 13y - 5.\]
While FOIL is a useful mnemonic for multiplying binomials, remember that it is simply a way to visualize the distributive property. The core principle is to multiply every term in the first polynomial by every term in the second polynomial. This principle extends to multiplying polynomials with more terms as well, though the FOIL acronym no longer directly applies. You can think of it as applying the distributive property repeatedly.
Determining Coefficients in the Product of Polynomials
Consider the product: \[\begin{align} (a_3 x^3+a_2 x^2&+a_1 x+a_0)(b_2 x^2+b_1 x+b_0)\\ =a_3b_2 x^5&+(a_3b_1+a_2b_2)x^4+(a_3b_0+a_2b_1+a_1b_2)x^3\\ &+(a_2b_0+a_1b_1+a_0b_2)x^2+(a_1b_0+a_0b_1)x+a_0b_0 \end{align}\]
The product is a polynomial in \(x\) whose degree is the sum of the degrees of the factors. The coefficient of each term can be obtained by the following rule:
For a term \(x^i\) , consider all possible products \(a_jb_k\) where \(a_j\) is the coefficient of \(x^j\) in the first polynomial and \(b_k\) is the coefficient of \(x^k\) in the second polynomial. The coefficient of \(x^i\) is the sum of all such products \(a_jb_k\) where \(j + k = i\) .
Thus, to obtain the coefficient of \(x^3\) , we find all products \(a_jb_k\) where \(j + k = 3\) . These are \(a_3b_0\) , \(a_2b_1\) , and \(a_1b_2\) . The coefficient of x³ is then \(a_3b_0+a_2b_1+a_1b_2\) .
This rule applies to the product of any two polynomials in x of the form \[a_mx^m+a_1x^{m-1}+\cdots +a_0\quad\text{and}\quad b_nx^n+b_{n-1}x^{n-1}+\cdots+b_0\] It also indicates how to obtain any particular coefficient of the product when the factors have numerical coefficients.
Example 1.14 . Find the coefficient of \(x^{100}\) in the product \[(a_{75}x^{75}+a_{74}x^{74}+\cdots+a_0)(b_{60}x^{60}+b_{59}x^{59}+\cdots+b_0)\]
Solution
The degree of the product is \(75 + 60 = 135\) . For the term \(x^{100}\) , we need \(j + k = 100\) . Since the powers in the first polynomial range from 0 to 75 and the powers in the second range from 0 to 60, the possible combinations for \(j+k = 100\) are: \(j=75\) and \(k=25\) , \(j=74\) and \(k=26\) ,..., \(j=40\) and \(k=60\) . Hence, the coefficient of \(x^100\) is \[a_{75}b_{25}+a_{74}b+{26}+\cdots+a_{40}b_{60}.\]
Similarly, the coefficient of \(x^{135}\) is \(a_{75}b_{60}\) .
Example 1.15 . Find the coefficient of \(x^3\) in the product \[(3x^4-2x^3+x^2-8x+7)(2x^3+5x^2+6x-3).\]
Solution
We look for \(j\) ( \(0\leq j\leq 4\) ) and \(k\) ( \(0\leq k\leq 3\) ) such that \(j+k=3\) . We have
| \(j\) | \(k\) | \(a_j b_k\) |
|---|---|---|
| \(3\) | \(0\) | \(a_3b_0=(-2)(-3)=6\) |
| \(2\) | \(1\) | \(a_2 b_1=(1)(6)=6\) |
| \(1\) | \(2\) | \(a_1 b_2=(-8)(5)=-40\) |
| \(0\) | \(3\) | \(a_0 b_3=(7)(2)=14\) |
The required coefficient is thus \[(-2)(-3) + (1)(6) + (-8)(5) + (7)(2)=-14.\]