Let \(A=x^{3}+2x^{2}-1\) and \(B=x^{2}-x+1\) . Then we can write \[A=BQ+R\] where \(Q=x+3\) and \(R=2x-4\) are called the quotient and the remainder, respectively. You may verify the above equation by expanding and simplifying the right hand side.
In general, if \(A\) and \(B\) are two polynomials such that the degree of \(A\) is greater than or equal to the degree of \(B\) , the process of finding two polynomial \(Q\) and \(R\) such that \[A=BQ+R\] and \(R\) is of lower degree than \(B\) , is called the process of dividing \(A\) by \(B\) . In this process, \(A\) is called the dividend, \(B\) the divisor, \(Q\) the quotient, and \(R\) the remainder. If \(R=0\) , we say \(A\) is divisible by \(B\) .
How the quotient is obtained is best explained in the following example.
Example 1.16 . Divide \(2x^{3}-32x-15\) by \(x-3\) and find the quotient and the remainder.
Solution
First we make sure that the dividend and the divisor are written in descending powers of \(x\) . Next we divide the first term of the dividend by the first term of the divisor \[\frac{2x^{3}}{x}=2x^{2}\] then multiply \(2x^{2}\) by the divisor and subtract the result from the dividend \[\begin{align} (2x^{3}-32x-15)-2x^{2}(x-3) & =\cancel{2x^{3}}-32x-15\cancel{-2x^{3}}+6x^{2}\\ & =6x^{2}-32x-15 \end{align}\] or using the long division we have 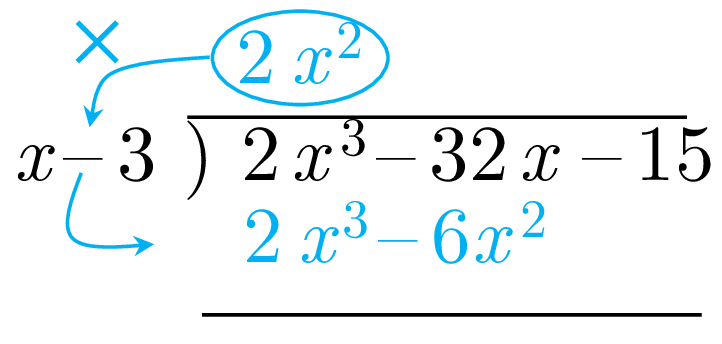
To simplify calculations, we can reverse the signs of the product of the multiplication and then add it to the dividend; namely 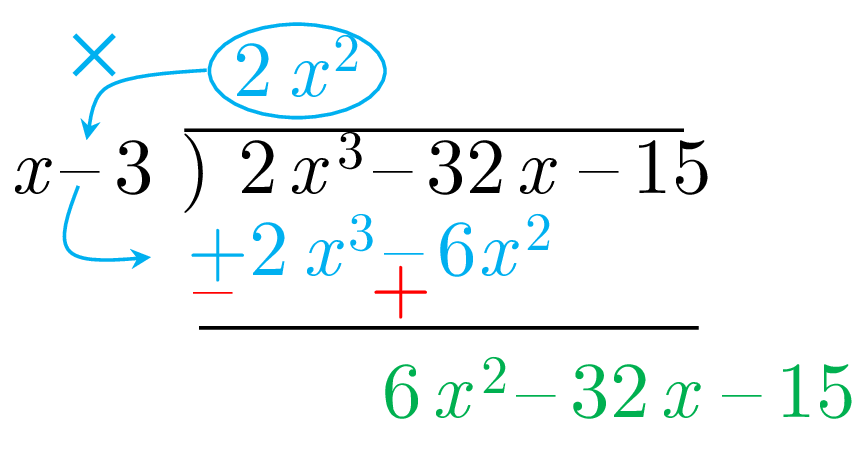
Now we divide \(6x^{2}-32x-15\) by \(x-3\) and follow the same steps; that is, we write it in descending power of \(x\) and divide its first term, \(6x^{2}\) , by the first term of the divisor, \(x\) : \(6x^{2}/x=6x\) 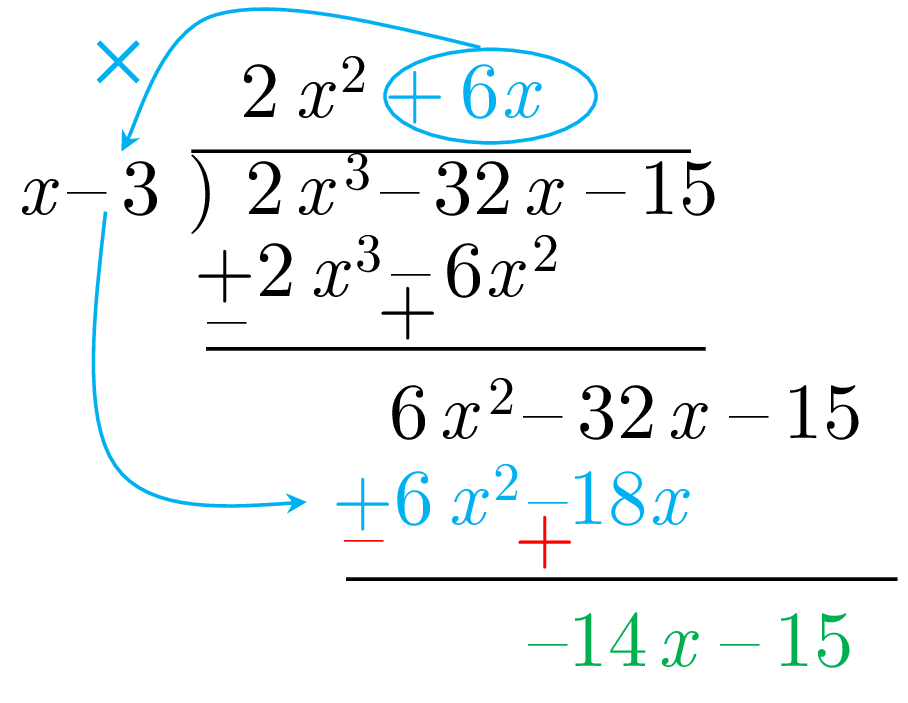
and again repeat until the degree of the remainder becomes less than the degree of the divisor 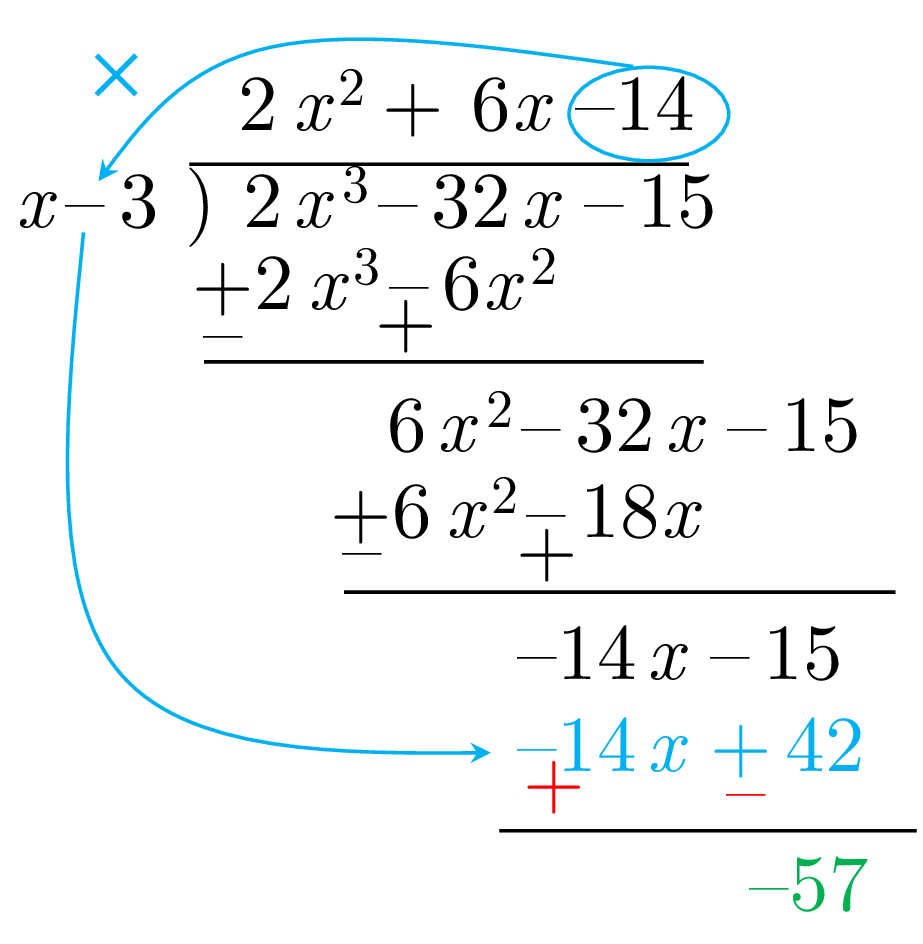
Therefore \[2x^{3}-32x-15=(x-3)(2x^{2}+6x-14)-57.\] Here the quotient is \(Q=2x^{2}+6x-14\) and the remainder is \(R=-57.\)
Example 1.17 . Divide \(x^{5}-4x^{3}+x^{2}+1\) by \(x^{2}+2x-1\) and find the quotient and the remainder
Solution
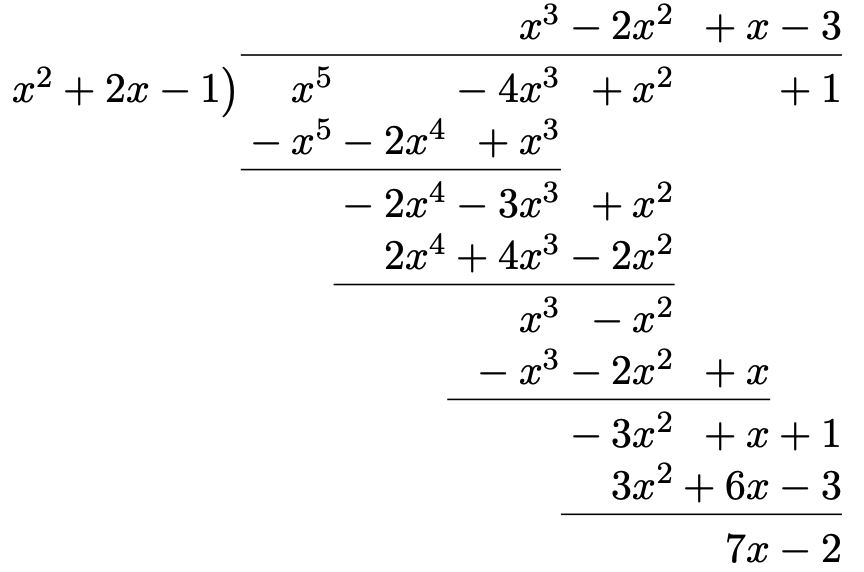
The quotient and the remainder are \(Q=x^{3}-2x^{2}+x-3\) and \(R=7x-2\) , respectively.