To solve nonlinear inequalities, we follow these steps:
- Transfer all terms to one side of the inequality sign and express the inequality in the form \[P>0,\qquad\text{or}\qquad P<0\] or \[P\geq0,\qquad\text{or}\qquad P\leq0\] where \(P\) is an expression in the variable (usually \(x\) ) [to indicate its dependence on \(x\) , we may write it as \(P(x)\) if we wish]
- Factor \(P\) \[P=Q_{1}Q_{2}\cdots Q_{n}\] where \(Q_{1},...,Q_{n}\) are expressions in \(x\) .
- Determine the zeros of each factor of \(P\) (find the values for which each \(Q_{i}\) is zero). These values divide the real line into intervals.
- Make a sign diagram (or sign table). Determine the sign of each factor in each interval.
- Determine the sign of \(P\) in each interval using the sign table. Recall that a product (or a quotient) that involves an even number of negative factors is positive and one that involves an odd number of negative factors is negative. If the inequality sign is \(\geq\) or \(\leq\) , pay attention to the endpoints of the intervals and check if they satisfy the inequality.
- For fractions; that is, when \[P=\frac{Q_{1}}{Q_{2}}\] we follow the same steps.
Table of Contents
How to Determine the Sign of Each Factor
To determine the sign of each factor, we can choose an arbitrary number (called a test value ) in that interval and find the sign of the factor. Alternatively you can use the following facts:
- If we have a factor of the form \(ax+b\)

- If we have a factor of the form \(ax^2+bx+c\) , then there are two cases:
If the equation \(ax^{2}+bx+c=0\) has two real solutions (or roots) \(r_{1}\) and \(r_{2}\) , then when \(x\) is between \(r_{1}\) and \(r_{2}\) , its sign is the opposite of the sign of \(a\) and outside that interval, its sign is the same as the sign of \(a\)
[ Because when \(ax^{2}+bx+c=0\) has two real solutions, then \[ax^{2}+bx+c=a(x-r_{1})(x-r_{2})\]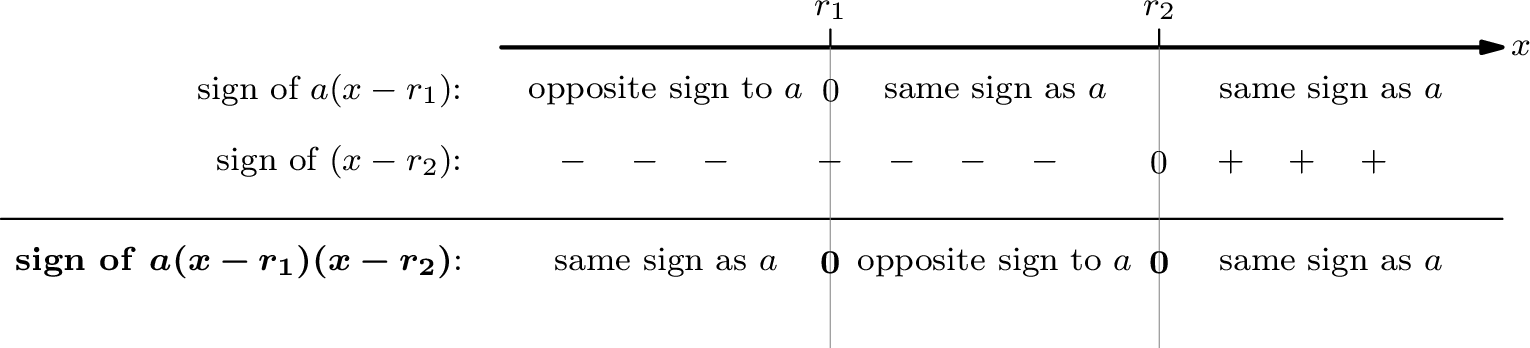
- If \(ax^{2}+bx+c=0\) does not have any real solutions (also known as roots), then its sign is always the same as the sign of \(a\)
Algebraic proof for why the sign of \(ax^2+bx+c\) is the same as \(a\) if there is no zeros
- Given : The quadratic equation \(ax^2 + bx + c = 0\) has no real solutions.
- Implication : The discriminant \(D = b^2 - 4ac\) satisfies \(D < 0\) .
- Objective : Show that \(ax^2 + bx + c\) is always positive if \(a > 0\) , and always negative if \(a < 0\) .
- Rewrite the Quadratic in Vertex Form : \[\begin{align} ax^2 + bx + c &= a\left(x^2 + \frac{b}{a}x\right) + c \\ &= a\left[\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a^2}\right] + c \\ &= a\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a} + c \\ &= a\left(x + \frac{b}{2a}\right)^2 + \left(c - \frac{b^2}{4a}\right). \end{align}\]
- Analyze the Components : The expression \(ax^2 + bx + c\) is now expressed as: \[a\underbrace{\left(x + \frac{b}{2a}\right)^2}_{\geq 0} + \underbrace{\left(c - \frac{b^2}{4a}\right)}_{\text{Constant}}.\]
- The term \(\left(x + \frac{b}{2a}\right)^2\) is always non-negative (a square is \(\geq 0\) ).
- The constant term \(c - \frac{b^2}{4a}\) is influenced by the discriminant \(D\) .
- Use the Discriminant Condition \(D < 0\) : From \(D = b^2 - 4ac < 0\) , we derive: \[b^2 < 4ac \quad \Rightarrow \quad c > \frac{b^2}{4a} \quad \text{if \( a > 0 \),} \quad \text{or} \quad c < \frac{b^2}{4a} \quad \text{if \( a < 0 \)}.\]
- Case 1 : If \(a > 0\) , then \(c - \frac{b^2}{4a} > 0\) . The quadratic becomes: \[a\left(\text{non-negative term}\right) + \text{positive constant} > 0 \quad \text{for all \( x \)}.\]
- Case 2 : If \(a < 0\) , then \(c - \frac{b^2}{4a} < 0\) . The quadratic becomes: \[a\left(\text{non-negative term}\right) + \text{negative constant} < 0 \quad \text{for all \( x \)}.\]
- Conclusion :
- When \(a > 0\) , the expression \(ax^2 + bx + c\) is a sum of non-negative and positive terms, so it is always positive .
- When \(a < 0\) , the expression is a sum of non-positive and negative terms, so it is always negative .
Summary The absence of real roots ( \(D < 0\) ) ensures the quadratic expression \(ax^2 + bx + c\) never crosses zero. Its sign is governed by the leading coefficient \(a\) , as shown by completing the square and analyzing the discriminant’s constraint. Thus: \[\text{Sign}(ax^2 + bx + c) = \text{Sign}(a) \quad \text{when \( D < 0 \)}.\]
Example 1. Solve \(x^{2}+6>5x\)
Solution
\[x^{2}+6>5x\] \[x^{2}-5x+6>0\tag{subtract $5x$}\] \[(x-2)(x-3)>0\tag{factor }\] Because the sign of a product depends on the signs of its factors, we need to determine where each factor is positive or negative. We identify that the zeros of these factors are \(x=2\) and \(x=3\) and using these values we construct the following sign table. Because the product is positive where both factors are positive or both are negative, the solutions are the real numbers in the union \((-\infty,2)\cup(3,\infty)\) or \[\{x|\ x<2\ \text{or}\ x>3\},\] as illustrated in the last row of the following sign table.
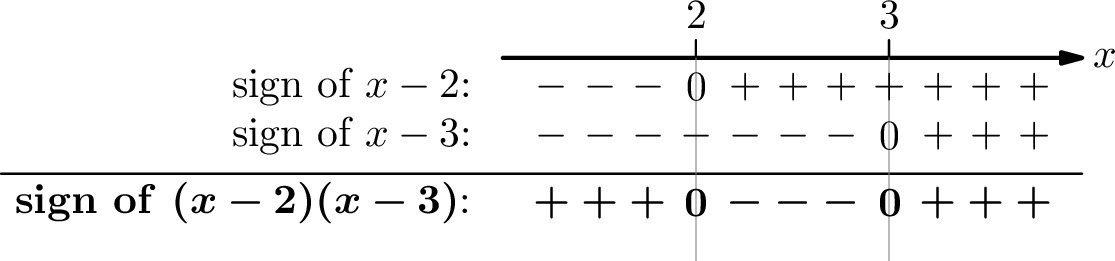
Alternatively because the multiple of \(x^{2}\) ( \(a=1\) ) is positive, as discussed above we know that when \(2
Example 2. Solve \(x^{3}+2x^{2}\le x+2\)
Solution
\[\begin{align} x^{3}+2x^{2} & \le x+2\tag{given inequality}\\ x^{3}+2x^{2}-x-2 & \le0\tag{move all terms to one side} \end{align}\] Now we need to factor \(x^{3}+2x^{2}-x-2\) . We can do that by grouping terms as follows \[\begin{align} x^{3}+2x^{2}-x-2 & =(x^{3}+2x^{2})-(x+2)\\ & =x^{2}(x+2)-(x+2)\\ & =(x+2)(x^{2}-1)\tag{factor out $(x+2)$}\\ & =(x+2)(x-1)(x+1)\tag{use the Difference of Squares formula in Section: Factorization} \end{align}\] So we need to find \(x\) such that \[(x+2)(x-1)(x+1)\le0\] To determine the sign, first we identify the zeros that are \(x=-2\) , \(x=-1\) , and \(x=1\) , and then construct the following sign table

The last row of the sign table is obtained from the fact that the polynomial is the product of the three factors. We read from this table that \((x+2)(x-1)(x+1)\) or \(x^{3}+2x^{2}-x-2\) is negative or zero on the interval \((-\infty,-2]\) and \([-1,1]\) . We have included \(x=-2\) and \(x=\pm1\) because at these points, the polynomial is zero and the inequality is satisfied. The solution set can be expressed as \[\{x|\ x\leq-2\quad\text{or}\quad-1\le x\leq1\}=(-\infty,2]\cup[-1,1].\]
Example 3. Solve \(\dfrac{x}{x+1}\leq2\) .
Solution
Recall that if we multiply both sides by a positive quantity, the direction of the inequality will be preserved but if we multiply both sides by a negative quantity, the direction of the inequality will be reversed. We do not know the sign of \(x+1\) , so if we wanted to multiply both sides by \(x+1\) , we would not be sure about the direction of the inequality. \[\begin{align} \frac{x}{x+1} & \leq2\tag{given inequality}\\ \frac{x}{x+1}-2 & \leq0\tag{subtract 2 from both sides}\\ \frac{x}{x+1}-\frac{2(x+1)}{x+1} & \leq0\tag{common denominator $(x+1)$}\\ \frac{x-2x-2}{x+1} & \le0\tag{combine fractions}\\ \frac{-x-2}{x+1} & \leq0\tag{simplify} \end{align}\] The sign of \((-2-x)/(x+1)\) is solely determined by the signs of \((-x-2)\) and \((x+1)\) . To construct the sign table, we need to identify the zeros of the numerator and denominator: \(x=-1\) and \(x=-2\) . These are the only values at which the fraction may change sign. Now we construct the following sign table.
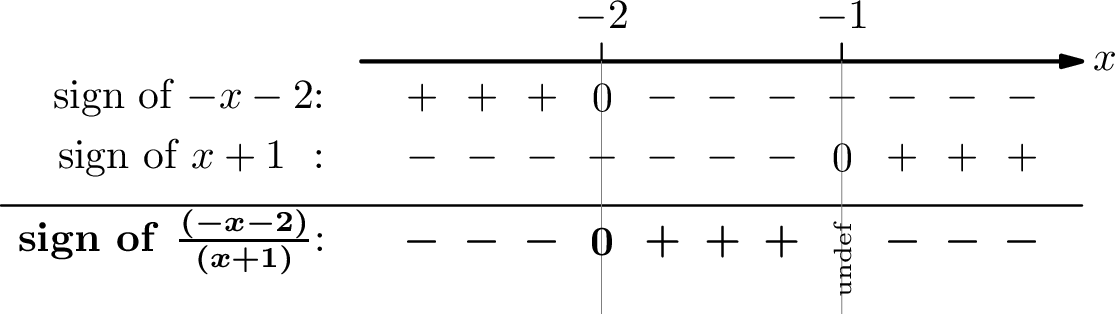
For \(x=-1\) , the denominator becomes zero, and because division by zero is not defined, we must eliminate \(x=-1\) from the set of acceptable solutions.
From the sign table, we read that \((-x-2)/(x+1)\leq0\) when \[x\le-2\qquad\text{or}\qquad x>-1\] and the solution set is \[(-\infty,-2]\cup(-1,\infty)\] We have included \(x=-2\) because for \(x=-2\) the numerator and hence the fraction are zero and the inequality is satisfied.
Example 4. Solve \(\dfrac{x+1}{x^{2}+1}>1\) .
Solution
\[\begin{align} \frac{x+1}{x^{2}+1} & >1\tag{given inequality}\\ \frac{x+1}{x^{2}+1}-1 & >0\tag{subtract $-1$ from both sides}\\ \frac{x+1}{x^{2}+1}-\underbrace{\frac{x^{2}+1}{x^{2}+1}}_1 & >0\tag{common denominator $(x^{2}+1)$}\\ \frac{x-x^{2}}{x^{2}+1} & >0\tag{combine fractions}\\ \frac{x(1-x)}{x^{2}+1} & >0\tag{factor} \end{align}\] Because \(x^{2}+1>0\) , the sign of the fraction is the same as the sign of the numerator \(x(1-x)\) . The zeros of the numerator are \(x=0\) and \(x=1\) that divide the real line into three intervals. Then we construct the sign table as follows.
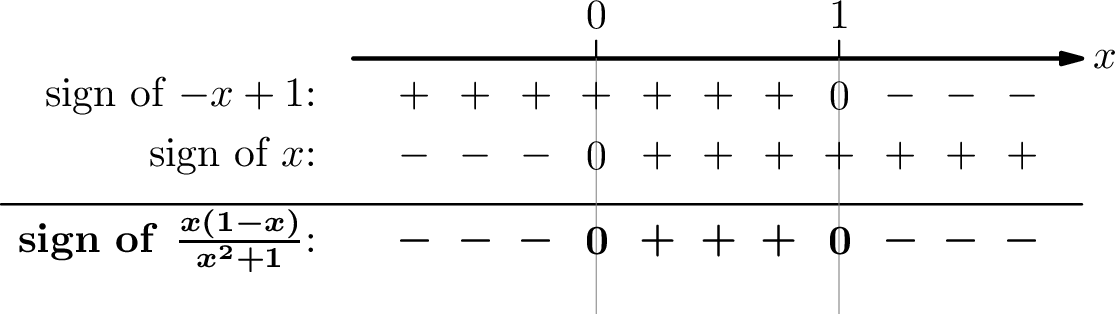
The sign table shows that \(x(1-x)/(x^{2}+1)>0\) when \(0