Let’s study the easiest type of curves in the plane: straight lines.

Slope of a Line

Consider a straight line \(L\) and two distinct points \(P(x_{1},y_{1})\) and \(Q(x_{2},y_{2})\) on it (the following figure). The slope of the line, often denoted by \(m\) , is defined to be the ratio \[\bbox[5px,border:1px solid black;background-color:#f2f2f2]{m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}.}\] 

• The slope of a line is independent of which two points on the line we choose.

If \(Q\) is one unit to the right of \(P\) such that \(x_{2}-x_{1}=1\) then \(m=y_{2}-y_{1}\) . This shows if we move one unit to the right from any point on a line, the signed distance that we have to go up or down to get back on the line is the slope of the line. This is why sometimes slope is written as \[\bbox[5px,border:1px solid black;background-color:#f2f2f2]{\text{slope}=\frac{\text{rise}}{\text{run}}.}\] 

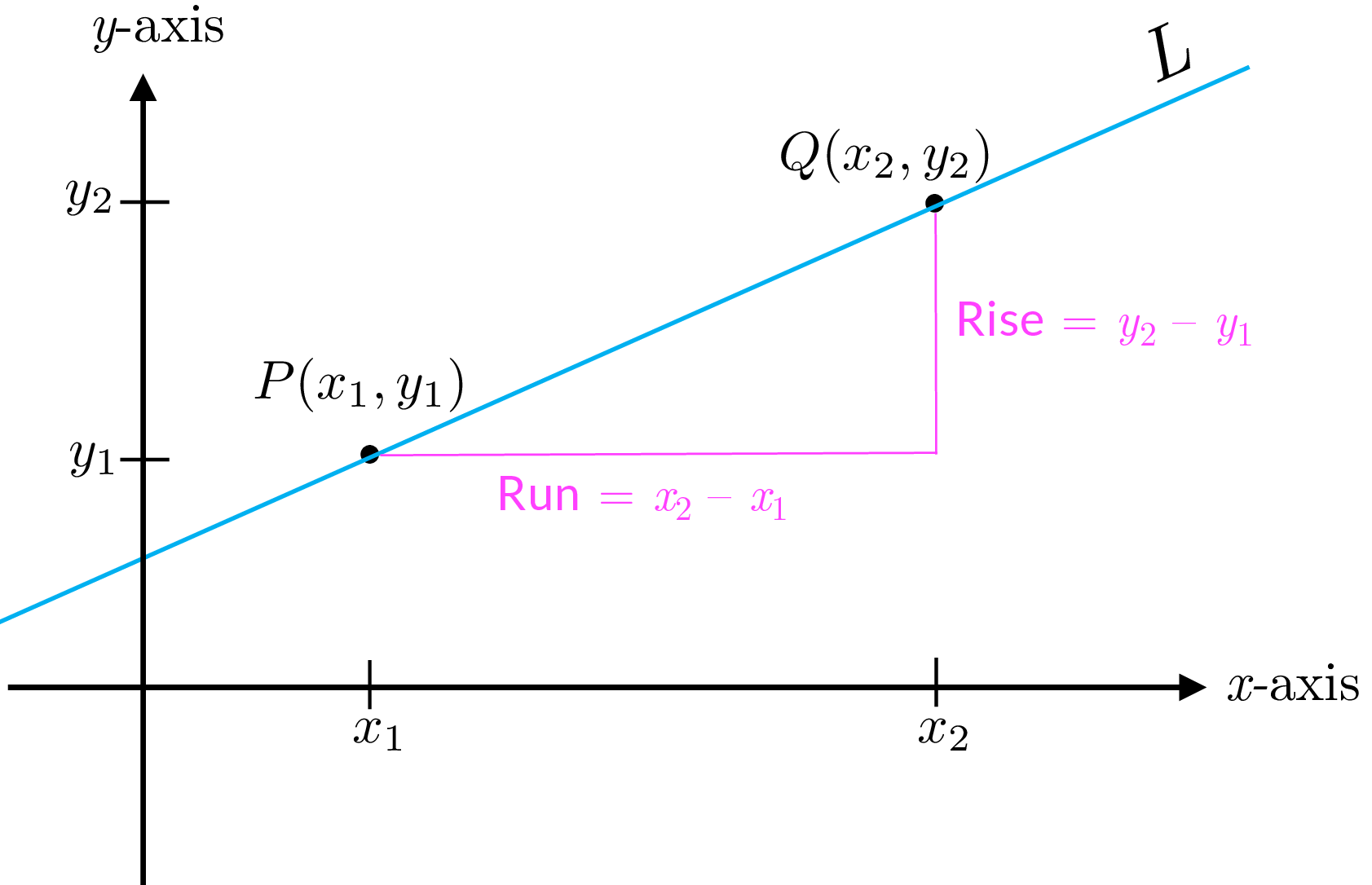
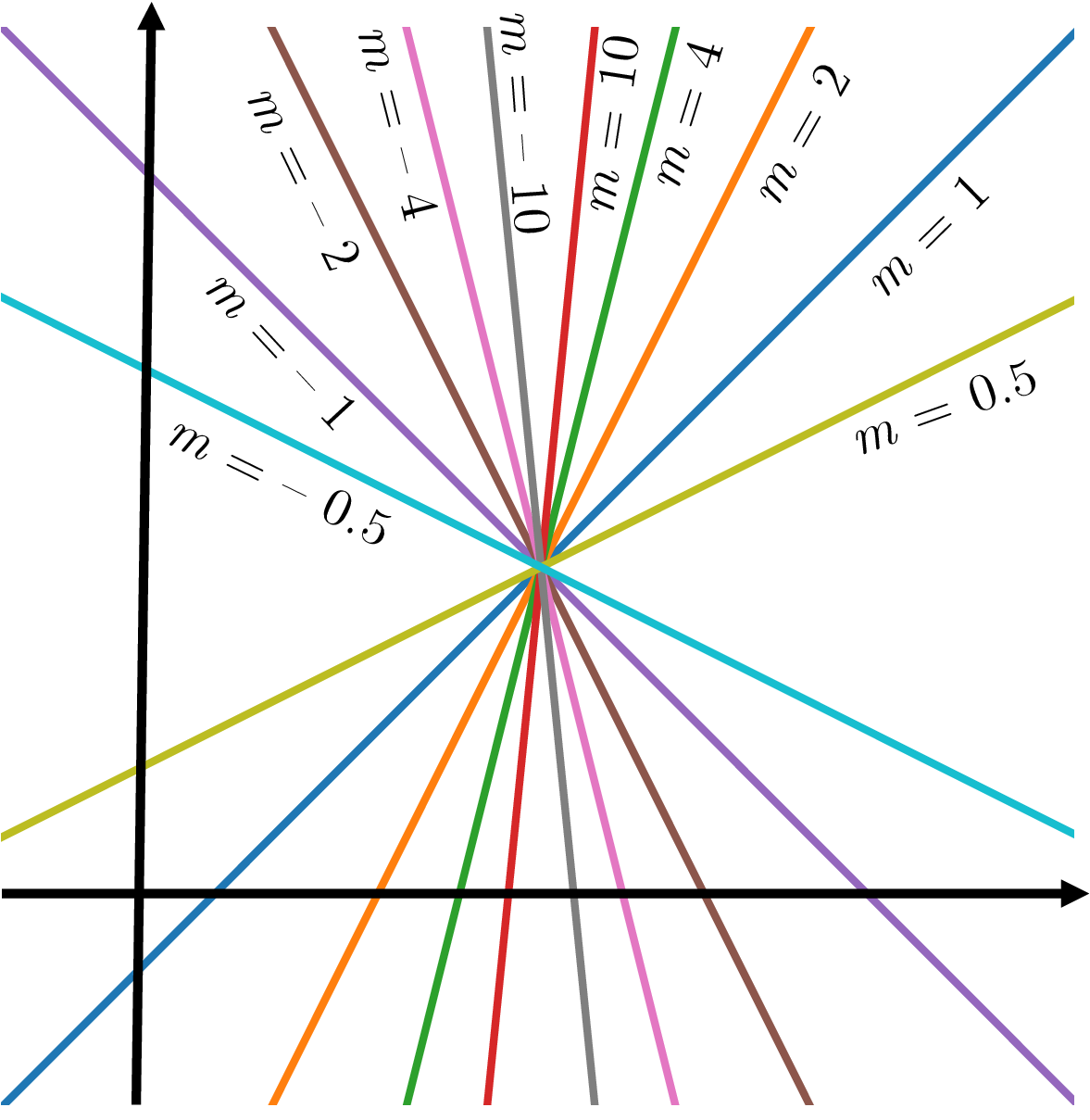
The sign of the slope is related to the direction of line as follows:

• \(m>0\) , the line rises to the right
• \(m<0\) , the line falls to the right
• \(m=0\) , line is horizontal

The absolute value of the slope is a measure of steepness of the line (See the following figure).

The slope of a vertical line is not defined, because any two points on such a line have the same \(x\) coordinates, and hence when we form the ratio \((y_{2}-y_{1})/(x_{2}-x_{1})\) the denominator becomes zero and division by zero is not defined. 

Equation of a Line

Now let’s find the equation of the line passing through a given point \(P(x_{1},y_{1})\) with slope \(m\) . If \((x,y)\) is any other point on this line, the slope formula gives \[\frac{y-y_{1}}{x-x_{1}}=m.\] That is, \[\bbox[5px,border:1px solid black;background-color:#f2f2f2]{y=y_{1}+m(x-x_{1}).}\] This equation is called the point-slope form of the equation of the line.

A special case of the above equation occurs when the given point is a point \((0,b)\) on the \(y\) -axis. In this case, the number \(b\) is called the \(y\) -intercept of the line and the equation of the line reduces to \[\bbox[5px,border:1px solid black;background-color:#f2f2f2]{y=mx+b,}\] which is called the slope-intercept form of the equation.

If we are given two points \((x_{1},y_{1})\) and \((x_{2},y_{2})\) on the line, then to find the equation of the line, we first have to calculate \(m\) which is \(m=(y_{2}-y_{1})/(x_{2}-x_{1})\) . Substitution of this expression for \(m\) in the point-slope form of the equation gives the point-point form : \[\bbox[5px,border:1px solid black;background-color:#f2f2f2]{y=y_{1}+\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)(x-x_{1})}\] 

• The equation of a vertical line through \((x_{1},y_{1})\) is \[\bbox[5px,border:1px solid black;background-color:#f2f2f2]{x=x_{1}.}\] 

General Equation of a Line

A linear equation in the variables \(x\) and \(y\) is an equation of the form: \[Ax + By + C = 0\] where \(A\) , \(B\) , and \(C\) are constants, and \(A\) and \(B\) are not both zero. Let’s see how this relates to familiar forms of lines:

• Nonvertical Line: A nonvertical line has the equation \(y = mx + b\) . We can rearrange this into the general form by subtracting \(mx + b\) from both sides: \(-mx + y - b = 0\) . This matches the general form \(Ax + By + C = 0\) with \(A = -m\) , \(B = 1\) , and \(C = -b\) .
• Vertical Line: A vertical line has the equation \(x = a\) . We can rearrange this into the general form by subtracting \(a\) from both sides: \(x - a = 0\) . This matches the general form \(Ax + By + C = 0\) with \(A = 1\) , \(B = 0\) , and \(C = -a\) .

Conversely, the graph of any linear equation \(Ax + By + C = 0\) (where A and B are not both zero) is a line. This means we can take the general form and manipulate it to find the more familiar slope-intercept or vertical line forms.

Manipulating the General Form: 

If we start with \(Ax + By + C = 0\) :

• If \(B \neq 0\) : We can solve for \(y\) :
  1. Subtract \(Ax\) and \(C\) from both sides: \(By = -Ax - C\)
  2. Divide by \(B\) : \(y = (-A/B)x + (-C/B)\) This is the slope-intercept form \(y = mx + b\) , with \(m = -A/B\) and \(b = -C/B\) .
• If \(B = 0\) : The equation becomes \(Ax + C = 0\) .
  1. Subtract \(C\) from both sides: \(Ax = -C\)
  2. Divide by \(A\) (since \(A\) cannot be zero if \(B\) is zero): \(x = -C/A\) This represents a vertical line \(x = a\) with \(a = -C/A\) .