Let \(f(x)\) be an expression in \(x\) . For example, \(f(x)=3x+2\) or \(f(x)=8x^{2}-\sqrt{x}+5\) . Where the graph of the equation \(y=f(x)\) crosses the \(y\) -axis is called the \(y\) -intercepts and where it crosses the \(x\) -axis is called the \(x\) -intercept.
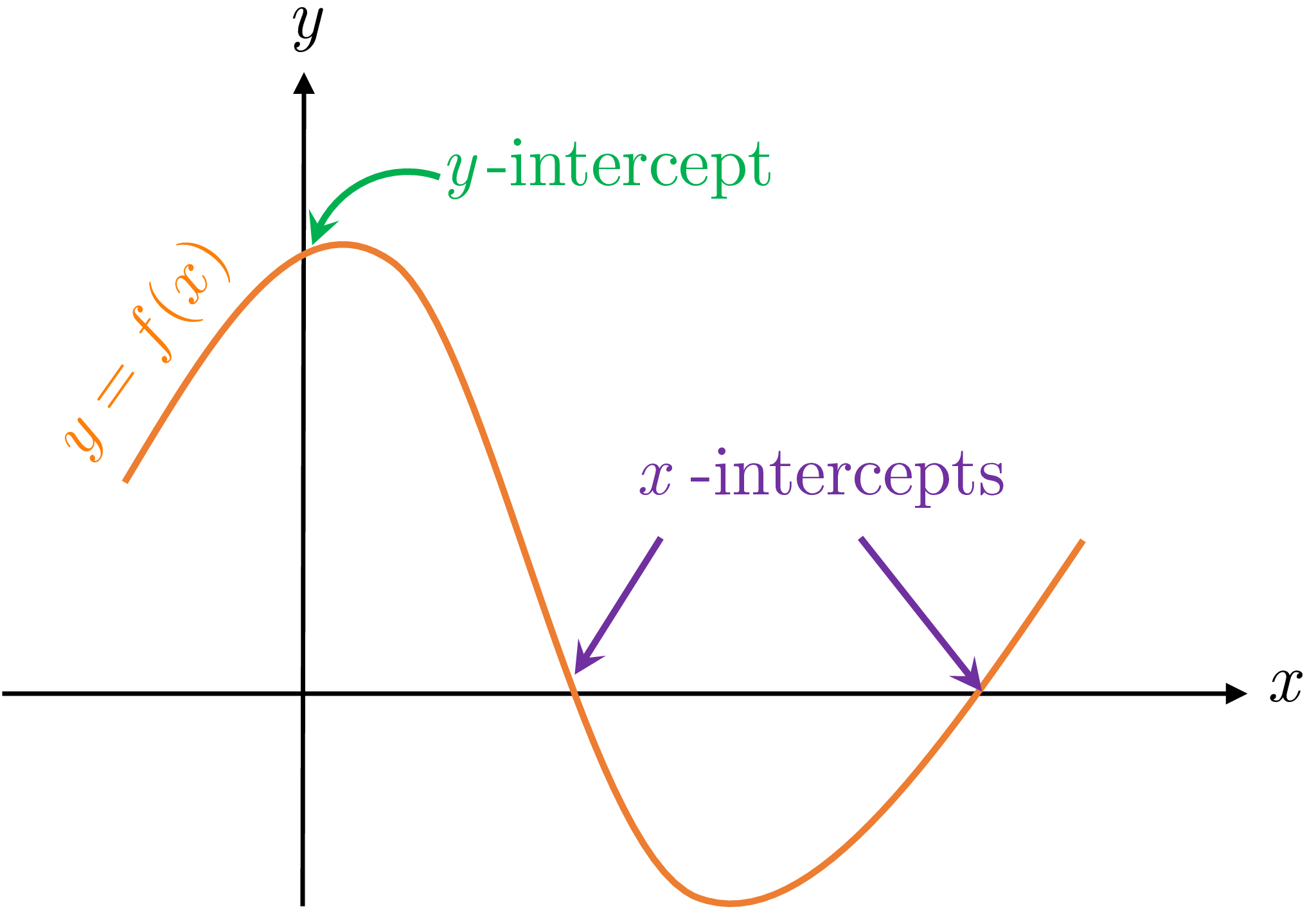
To find the \(x\) -intercept of the graph of \(y=f(x)\) , we set \(y=0\) and solve for \(x\) . Therefore, the \(x\) -intercepts of the graph of \(y=f(x)\) are solutions to \(f(x)=0\) (also called the roots of \(f\) ).
Similarly to find the \(y\) -intercept, we substitute \(x=0\) in the equation \(y=f(x)\) and solve for \(y\) .