The following theorem provides the formula for the distance between a point and a line:
Theorem 3.1 . The distance between the point \(P\left(x_{0}, y_{0}\right)\) and the line \(L\) with equation \[a x+b y+c=0\] is given by \[d=\frac{\left|a x_{0}+b y_{0}+c\right|}{\sqrt{a^{2}+b^{2}}}\]
Proof
Drop a perpendicular \(L_1\) from \(P\) to \(L\) and call the foot of the perpendicular \(Q\left(x_{1}, y_{1}\right)\) . Because the slope of \(L\) is \(-\frac{a}{b}\) , the slope of \(L_1\) is \(\frac{b}{a}\) . Since \(P\left(x_{0}, y_{0}\right)\) lies on \(L_1\) , the equation of \(L_1\) is \[y-y_{0}=\frac{b}{a}\left(x-x_{0}\right)\]
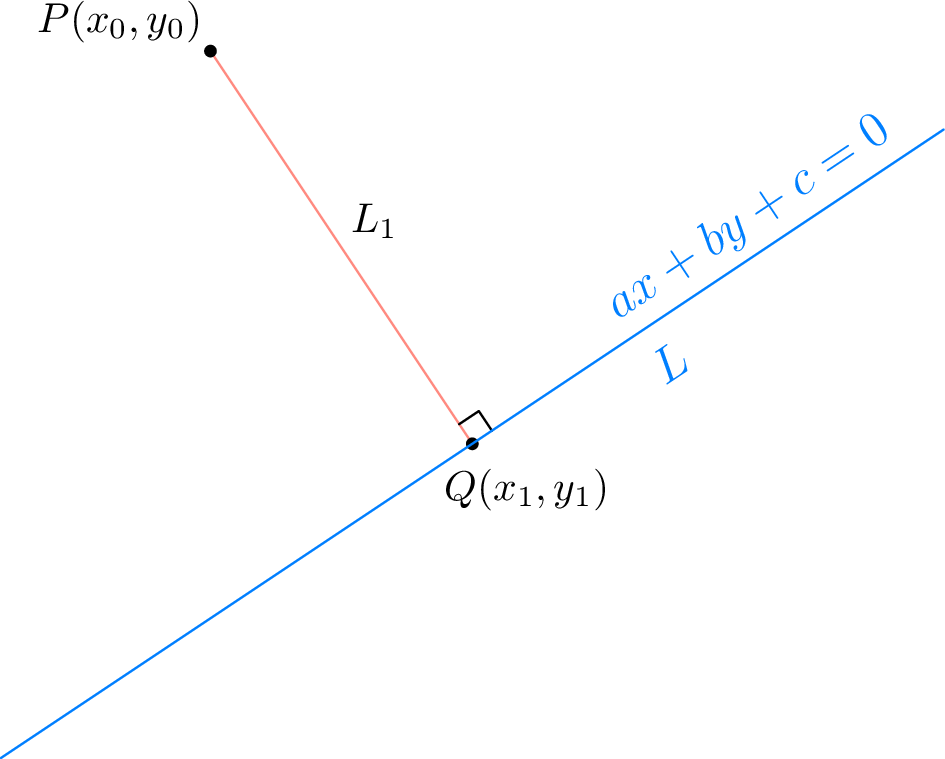
Because \(Q\left(x_{1}, y_{1}\right)\) is also on \(L_1\) , we have \[y_{1}-y_{0}=\frac{b}{a}\left(x_{1}-x_{0}\right)\] or \[\frac{y_{1}-y_{0}}{b}=\frac{x_{1}-x_{0}}{a} .\]
Let’s denote the above ratio by \(r\) . Then we have \[x_{1}-x_{0}=a r \quad \text { and } \quad y_{1}-y_{0}=b r\] and therefore \[\begin{align} d=|P Q| & =\sqrt{\left(x_{1}-x_{0}\right)^{2}+\left(y_{1}-y_{0}\right)^{2}} \\ & =\sqrt{a^{2} r^{2}+b^{2} r^{2}} \\ & =\sqrt{a^{2}+b^{2}}|r| \end{align}\]
To find \(r\) , we use the fact that \(Q\left(x_{1}, y_{1}\right)\) lies on \(L\) and therefore \(\left(x_{1}, y_{1}\right)\) satisfies the equation of \(L\) , ie. \[a x_{1}+b y_{1}+c=0.\] Because \(x_{1}=a r+x_{0}\) and \(y_{1}=b r+y_{0}\) , we have \[a\left(a r+x_{0}\right)+b\left(b r+y_{0}\right)+c=0\] or \[\begin{align} a^{2} r+b^{2} r & =-\left(a x_{0}+b y_{0}+c\right) \\ \Rightarrow r & =-\frac{a x_{0}+b y_{0}+c}{a^{2}+b^{2}} \end{align}\]
Finally, substituting \(|r|\) in the formula for \(d\) , we obtain \[\begin{align} d=|P Q| & =\sqrt{a^{2}+b^{2}}|r| \\ & =\sqrt{a^{2}+b^{2}} \frac{\left|a x_{0}+b y_{0}+c\right|}{a^{2}+b^{2}} \\ & =\frac{\left|a x_{0}+b y_{0}+c\right|}{\sqrt{a^{2}+b^{2}}} \end{align}\]
- In the above theorem, we have assumed that \(a \neq 0\) and \(b \neq 0\) . However, we can verify that the formula for the distance between a point and a line continues to work if either \(a=0\) or \(b=0\) .
Example 1. Find the distance between the point \((3,-1)\) and the line \(y=2 x-1\) .
Solution
We write the equation of the line as \[2 x-y-1=0.\] Then it follows from the above theorem that the distance between the point and the line is \[d=\frac{|2(3)-(-1)-1|}{\sqrt{2^{2}+(-1)^{2}}}=\frac{6}{\sqrt{5}}.\]
Example 2. Find the distance between the straight lines \(3x-4y+10=0\) and \(3x-4y-5=0\) .
Solution
Since the slopes of these two lines are the same, to determine the distance between them, we can choose an arbitrary point on one of them and then find the distance between this point and the other line.
For example, if we set \(x=3\) , from the equation of the second line we will find \[3\times 3-4y-5=0 \Rightarrow y=1\] In other words, the pont \((3,1)\) is on the second line. Now we calculate the distance between \((3,1)\) and the first line whose equation is \(3x-4y+10=0\) : \[d=\frac{|3\times 3 -4\times 1+10|}{\sqrt{3^2+3^2}}=\frac{15}{5}=3.\] Therefore, the distance between these two lines is 3.