Significado Geométrico de la Diferenciación
Es útil considerar qué significado geométrico se le puede dar a la derivada.
En primer lugar, cualquier función de \(x\), tal, por ejemplo, como \(x^2\), o \(\sqrt{x}\), o \(ax+b\), puede ser dibujada como una curva; y hoy en día, muchos estudiantes están familiarizados con el proceso de trazado de curvas. Existen varias herramientas para trazar curvas, como calculadoras gráficas, Wolfram Alpha,1 MATLAB, Python, o incluso Microsoft Excel.
Sea \(PQR\), en la siguiente figura, una porción de una curva dibujada con respecto a los ejes \(x\) y \(y\). Considere cualquier punto \(Q\) en esta curva con coordenadas \((x,y)\) (es decir, la abscisa del punto es \(x\) y su ordenada es \(y\)).
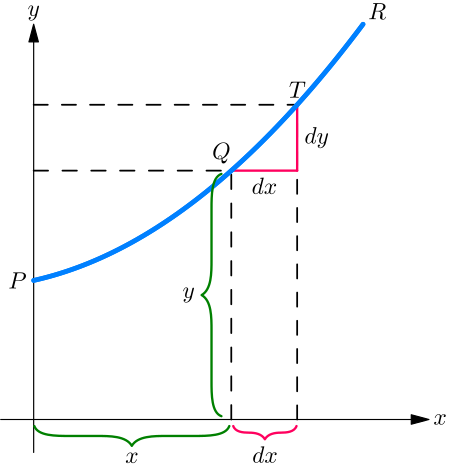
Ahora observe cómo \(y\) cambia cuando \(x\) varía. Si \(x\) se incrementa en un pequeño incremento \(dx\), hacia la derecha, se observará que \(y\) también (en esta curva particular) aumenta en un pequeño incremento \(dy\) (porque esta curva particular resulta ser una curva ascendente). Entonces, la razón de \(dy\) a \(dx\) es una medida del grado en que la curva está inclinada hacia arriba entre los dos puntos \(Q\) y \(T\). De hecho, se puede ver en la figura que la curva entre \(Q\) y \(T\) tiene muchas pendientes diferentes, por lo que no podemos hablar precisamente de la pendiente de la curva entre \(Q\) y \(T\). Sin embargo, si \(Q\) y \(T\) están tan cerca entre sí que la pequeña porción \(QT\) de la curva es prácticamente recta, entonces es cierto decir que la razón \(\dfrac{dy}{dx}\) es la pendiente de la curva a lo largo de \(QT\). La línea recta \(QT\) que se produce en cualquiera de los lados toca la curva a lo largo de la porción \(QT\) solamente, y si esta porción es indefinidamente pequeña, la línea recta tocará la curva en prácticamente un solo punto, y será por tanto una tangente a la curva.
Esta tangente a la curva tiene evidentemente la misma pendiente que \(QT\), de modo que \(\boldsymbol{\dfrac{dy}{dx}}\) es la pendiente de la tangente a la curva en el punto \(Q\) para el cual se encuentra el valor de \(\boldsymbol{\dfrac{dy}{dx}}\).
Hemos visto que la breve expresión "la pendiente de una curva" no tiene un significado preciso, porque una curva tiene muchas pendientes; de hecho, cada pequeña porción de una curva tiene una pendiente diferente. Sin embargo, "la pendiente de una curva en un punto" es una cosa perfectamente definida; es la pendiente de una porción muy pequeña de la curva situada justo en ese punto; y hemos visto que esto es lo mismo que "la pendiente de la tangente a la curva en ese punto."
La pendiente de una curva en un punto es la pendiente de la tangente a la curva en ese punto.
Observe que \(dx\) es un pequeño paso hacia la derecha, y \(dy\) el correspondiente pequeño paso hacia arriba. Estos pasos deben considerarse tan cortos como sea posible, de hecho indefinidamente cortos, aunque en los diagramas debemos representarlos con trozos que no son infinitesimalmente pequeños, de lo contrario no podrían verse.
A partir de ahora haremos un uso considerable de esta circunstancia de que \(\boldsymbol{\dfrac{dy}{dx}}\) representa la pendiente de la curva en cualquier punto.
Si una curva está inclinada hacia arriba a \(45^\circ\) en un punto particular, como en la siguiente figura, \(dy\) y \(dx\) serán iguales, y el valor de \(\dfrac{dy}{dx} = 1\).
Si la curva se inclina más pronunciada que \(45^\circ\) (siguiente figura), \(\dfrac{dy}{dx}\) será mayor que \(1\).
Si la curva se inclina muy suavemente, como en la siguiente figura, \(\dfrac{dy}{dx}\) será una fracción menor que \(1\).
Para una línea horizontal, o un lugar horizontal en una curva, \(dy=0\), y por lo tanto \(\dfrac{dy}{dx}=0\).
Si una curva se inclina hacia abajo, como en la siguiente figura, \(dy\) será un paso hacia abajo, y por lo tanto debe considerarse de valor negativo; por lo tanto, \(\dfrac{dy}{dx}\) tendrá también un signo negativo.
Si la "curva" resulta ser una línea recta, como la que sigue en la figura siguiente, el valor de \(\dfrac{dy}{dx}\) será el mismo en todos los puntos a lo largo de ella. En otras palabras, su pendiente es constante.
Si una curva es aquella que gira más hacia arriba a medida que avanza hacia la derecha, los valores de \(\dfrac{dy}{dx}\) serán cada vez mayores con el aumento de la inclinación, como en la figura siguiente.
Si una curva es una que se hace cada vez más plana a medida que avanza, los valores de \(\dfrac{dy}{dx}\) se harán cada vez más pequeños a medida que se alcance la parte más plana, como en la siguiente figura.
Si una curva primero desciende y luego sube nuevamente, como en la siguiente figura, presentando una concavidad hacia arriba, entonces claramente \(\dfrac{dy}{dx}\) primero será negativo, con valores decrecientes a medida que la curva se aplana, luego será cero en el punto donde se alcanza el fondo del valle de la curva; y desde este punto en adelante \(\dfrac{dy}{dx}\) tendrá valores positivos que seguirán aumentando. En tal caso, se dice que \(y\) pasa por un mínimo. El valor mínimo de \(y\) no es necesariamente el valor más pequeño de \(y\), es el valor de \(y\) correspondiente al fondo del valle; por ejemplo, en la siguiente figura, el valor de \(y\) correspondiente al fondo del valle es \(1\), mientras que \(y\) toma en otras partes valores que son menores que este. La característica de un mínimo es que \(y\) debe aumentar a ambos lados de él.
Nota—Para el valor particular de \(x\) que hace que \(y\) sea un mínimo, el valor de \(\dfrac{dy}{dx} = 0\).
Si una curva primero asciende y luego desciende, los valores de \(\dfrac{dy}{dx}\) serán positivos al principio; luego cero, al alcanzar la cima; luego negativos, a medida que la curva desciende, como en la siguiente figura. En este caso, se dice que \(y\) pasa por un máximo, pero el valor máximo de \(y\) no es necesariamente el valor más grande de \(y\). En la figura anterior, el máximo de \(y\) es \(2\frac{1}{3}\), pero esto no es de ninguna manera el valor más grande que \(y\) puede tener en algún otro punto de la curva.
Nota—Para el valor particular de \(x\) que hace que \(y\) sea un máximo, el valor de \(\dfrac{dy}{dx}= 0\).
Si una curva tiene la peculiar forma de la siguiente figura, los valores de \(\dfrac{dy}{dx}\) siempre serán positivos; pero habrá un lugar particular donde la pendiente es menos pronunciada, donde el valor de \(\dfrac{dy}{dx}\) será un mínimo; es decir, menor que en cualquier otra parte de la curva.
Si una curva tiene la forma de la siguiente figura, el valor de \(\dfrac{dy}{dx}\) será negativo en la parte superior y positivo en la parte inferior; y en la nariz de la curva, donde se vuelve realmente perpendicular, el valor de \(\dfrac{dy}{dx}\) será infinitamente grande.
En resumen:
Cuando \(x\) aumenta
Si \(\dfrac{dy}{dx}>0\), \(\qquad y\) aumenta; la curva asciende hacia la derecha.
Si \(\dfrac{dy}{dx}<0\), \(\qquad y\) disminuye; la curva desciende hacia la derecha.
Ahora que entendemos que \(\dfrac{dy}{dx}\) mide la inclinación de una curva en cualquier punto, consideremos alguna de las ecuaciones que ya hemos aprendido a diferenciar.
Ejemplo 10.1. Como el caso más simple, tomemos esto: \[y=x+b.\]
Se traza en la siguiente figura, usando escalas iguales para \(x\) y \(y\). Si ponemos \(x = 0\), entonces la ordenada correspondiente será \(y = b\); es decir, la “curva” cruza el eje \(y\) a la altura \(b\). Desde aquí asciende a \(45^\circ\); para los valores que demos a \(x\) a la derecha, tenemos un \(y\) igual para ascender. La línea tiene un gradiente de \(1\) en \(1\).
Ahora diferenciamos \(y = x+b\), con las reglas que ya hemos aprendido, y obtenemos \(\dfrac{dy}{dx} = 1\).
La pendiente de la línea es tal que por cada pequeño paso \(dx\) hacia la derecha, subimos un pequeño paso igual \(dy\) hacia arriba. Y esta pendiente es constante, siempre la misma pendiente.
Ejemplo 10.2. Tomemos otro caso: \[y = ax+b.\] Sabemos que esta curva, al igual que la anterior, comenzará desde una altura \(b\) en el eje \(y\). Pero antes de dibujar la curva, determinemos su pendiente diferenciando; lo que da \(\dfrac{dy}{dx} = a\). La pendiente será constante, en un ángulo cuyo tangente aquí se llama \(a\). Asignemos a \(a\) algún valor numérico, digamos \(\frac{1}{3}\). Entonces debemos darle tal pendiente que ascienda \(1\) en \(3\); o \(dx\) será \(3\) veces más grande que \(dy\); como se amplía en la siguiente figura.
Entonces, dibuje la línea en la siguiente figura con esta pendiente.
Ahora para un caso un poco más difícil.
Ejemplo 10.3. Sea \[y= ax^2 + b.\]
Nuevamente, la curva comenzará en el eje \(y\) a una altura \(b\) por encima del origen.
Ahora diferenciamos. [Si lo ha olvidado, vuelva atrás; o, más bien, no retroceda, sino que piense en la diferenciación.] \[\frac{dy}{dx} = 2ax.\]
Esto muestra que la inclinación no será constante: aumenta a medida que \(x\) aumenta. En el punto de inicio \(P\), donde \(x = 0\), la curva (figura siguiente) no tiene inclinación, es decir, está nivelada. A la izquierda del origen, donde \(x\) tiene valores negativos, \(\dfrac{dy}{dx}\) también tendrá valores negativos, o descenderá de izquierda a derecha, como en la Figura.
Ilustremos esto resolviendo un caso particular. Tomando la ecuación \[y = \frac{1}{4}x^2 + 3,\] y diferenciándola, obtenemos \[\dfrac{dy}{dx} = \frac{1}{2}x.\] Ahora asigne algunos valores sucesivos, digamos de \(0\) a \(5\), a \(x\); y calcule los valores correspondientes de \(y\) por la primera ecuación; y de \(\dfrac{dy}{dx}\) de la segunda ecuación. Tabulando resultados, tenemos:
| \(x\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|---|
| \(y\) | \(3\) | \(3\frac{1}{4}\) | \(4\) | \(5\frac{1}{4}\) | \(7\) | \(9\frac{1}{4}\) |
| \(\dfrac{dy}{dx}\) | \(0\) | \(\frac{1}{2}\) | \(1\) | \(1\frac{1}{2}\) | \(2\) | \(2\frac{1}{2}\) |
Luego, trácenlos en dos curvas, Fig. 10.18 y Fig. 10.19; en Fig. 10.18 trace los valores de \(y\) contra los de \(x\) y en Fig. 10.19 aquellos de \(\dfrac{dy}{dx}\) contra los de \(x\). Para cualquier valor asignado de \(x\), la altura de la ordenada en la segunda curva es proporcional a la pendiente de la primera curva.
Si una curva llega a un cúspide repentina, como en la figura siguiente, la pendiente en ese punto cambia repentinamente de una pendiente ascendente a una descendente. En ese caso \(\dfrac{dy}{dx}\) claramente experimentará un cambio abrupto de un valor positivo a un valor negativo.
Los siguientes ejemplos muestran más aplicaciones de los principios explicados.
Ejemplo 10.4. (a) Encuentre la pendiente de la tangente a la curva \[y = \frac{1}{2x} + 3,\] en el punto donde \(x = -1\). (b) Encuentre el ángulo que esta tangente forma con la curva \(y = 2x^2 + 2\).
Solución. (a) La pendiente de la tangente es la pendiente de la curva en el punto donde se tocan entre sí; es decir, es el \(\dfrac{dy}{dx}\) de la curva para ese punto. Aquí \(\dfrac{dy}{dx} = -\dfrac{1}{2x^2}\) y para \(x = -1\), \(\dfrac{dy}{dx} = -\dfrac{1}{2}\), que es la pendiente de la tangente y de la curva en ese punto. La tangente, siendo una línea recta, tiene por ecuación \(y = ax + b\), y su pendiente es \(\dfrac{dy}{dx} = a\), por lo tanto \(a = -\dfrac{1}{2}\). Además, si \(x= -1\), \(y = \dfrac{1}{2(-1)} + 3 = 2\frac{1}{2}\); y como la tangente pasa por este punto, las coordenadas del punto deben satisfacer la ecuación de la tangente, a saber \[y = -\dfrac{1}{2} x + b,\] de modo que \(2\frac{1}{2} = -\dfrac{1}{2} \times (-1) + b\) y \(b = 2\); la ecuación de la tangente es por tanto \(y = -\dfrac{1}{2} x + 2\) (véase la figura siguiente).
(b) Ahora, cuando dos curvas se encuentran, la intersección es un punto común a ambas curvas, sus coordenadas deben satisfacer la ecuación de cada una de las dos curvas; es decir, debe ser una solución del sistema de ecuaciones simultáneas formadas al juntar las ecuaciones de las curvas. Aquí las curvas se encuentran entre sí en puntos dados por la solución de \[\left\{ \begin{align} y &= 2x^2 + 2, \\ y &= -\frac{1}{2} x + 2 \quad\text{o}\quad 2x^2 + 2 = -\frac{1}{2} x + 2; \end{align} \right.\]
es decir, \[x(2x + \frac{1}{2}) = 0.\]
Esta ecuación tiene por soluciones \(x = 0\) y \(x = -\frac{1}{4}\) (véase la figura siguiente). La pendiente de la curva \(y = 2x^2 + 2\) en cualquier punto es \[\dfrac{dy}{dx} = 4x.\]
Para el punto donde \(x = 0\), esta pendiente es cero; la curva es horizontal. Para el punto donde \[x = -\dfrac{1}{4},\quad \dfrac{dy}{dx} = -1;\] por lo tanto, la curva en ese punto se inclina hacia abajo a la derecha en tal ángulo \(\theta\) con la horizontal que \(\tan \theta = 1\); es decir, a \(45^\circ\) con la horizontal.
La pendiente de la línea recta es \(-\frac{1}{2}\); es decir, se inclina hacia abajo a la derecha y forma con la horizontal un ángulo \(\phi\) tal que \(\tan \phi = \frac{1}{2}\); es decir, un ángulo de \(26^\circ~34'\). Se sigue que en el primer punto la curva corta la línea recta en un ángulo de \(26^\circ~34'\), mientras que en el segundo la corta en un ángulo de \(45^\circ - 26^\circ~34' = 18^\circ~26'\) (véase la figura siguiente).
Ejemplo 10.5. Se va a dibujar una línea recta, a través de un punto cuyas coordenadas son \(x = 2\), \(y = -1\), como tangente a la curva \(y = x^2 - 5x + 6\). Encuentre las coordenadas del punto de contacto.
Nota.—-el punto \((2,-1)\) no se encuentra en la curva \(y=x^2-5x+6\).
Solución. La pendiente de la tangente debe ser la misma que el \(\dfrac{dy}{dx}\) de la curva; es decir, \(2x - 5\).
La ecuación de la línea recta es \(y = ax + b\), y como se satisface para los valores \(x = 2\), \(y = -1\), entonces \(-1 = a\times2 + b\); además, su \(\dfrac{dy}{dx} = a = 2x - 5\) [dado que \(y=ax+b\) es la línea tangente, su pendiente, \(a\), debe ser la misma que \(\dfrac{d(x^2-5x+6)}{dx}\)].
El \(x\) y el \(y\) del punto de contacto también deben satisfacer tanto la ecuación de la tangente como la ecuación de la curva.
Tenemos entonces \[\left\{\begin{align} y &= x^2 - 5x + 6, &&\text{(i)} \\ y &= ax + b, &&\text{(ii)} \\ -1 &= 2a + b, &&\text{(iii)} \\ a &= 2x - 5, &&\text{(iv)} \end{align}\right.\] cuatro ecuaciones en \(a\), \(b\), \(x\), \(y\).
Las ecuaciones (i) y (ii) dan \(x^2 - 5x + 6 = ax+b\).
Reemplazando \(a\) y \(b\) por su valor en esto, obtenemos \[x^2 - 5x + 6 = (2x - 5)x - 1 - 2(2x - 5),\] que simplifica a \(x^2 - 4x + 3 = 0\), cuyas soluciones son: \(x = 3\) y \(x = 1\). Reemplazando en (i), obtenemos \(y = 0\) y \(y = 2\) respectivamente; los dos puntos de contacto son entonces \(x = 1\), \(y = 2\), y \(x = 3\), \(y = 0\) (véase la figura siguiente).
Nota.—En todos los ejercicios relacionados con curvas, los estudiantes encontrarán extremadamente instructivo verificar las deducciones obtenidas trazando realmente las curvas.
Ejercicios
Ejercicio 10.1. Traza la curva \(y = \dfrac{3}{4} x^2 - 5\), usando escalas iguales para \(x\) y \(y\). Mida en puntos correspondientes a diferentes valores de \(x\), el ángulo de su pendiente.
Encuentre, diferenciando la ecuación, la expresión para la pendiente; y verifique, a partir de una Tabla de Tangentes Naturales, si esto coincide con el ángulo medido.
Solución
\[y=\frac{3}{4} x^2 - 5 \Rightarrow \frac{dy}{dx}=\frac{3}{2}x\]
Cuando \(x=-3\), \(\dfrac{dy}{dx}=-\dfrac{9}{2}\)
del gráfico: pendiente de la línea tangente \(=\dfrac{-9}{2}=-4.5\). Coinciden.
Cuando \(x=-2\), \(\dfrac{dy}{dx}=-3\)
del gráfico: pendiente de la línea tangente \(=\dfrac{-6}{2}=-3\). Coinciden.
Cuando \(x=-1\), \(\dfrac{dy}{dx}=-\dfrac{3}{2}\)
del gráfico: pendiente de la línea tangente \(=\dfrac{-3}{2}=-1.5\). Coinciden.
Cuando \(x=0\), \(\dfrac{dy}{dx}=0\)
del gráfico: la línea tangente es horizontal. Así que su pendiente es cero. Coinciden.
Cuando \(x=1\), \(\dfrac{dy}{dx}=\dfrac{3}{2}\)
del gráfico: pendiente de la línea tangente \(=\dfrac{3}{2}=1.5\). Coinciden.
Cuando \(x=2\), \(\dfrac{dy}{dx}=3\)
del gráfico: pendiente de la línea tangente \(=\dfrac{6}{2}=3\). Coinciden.
Cuando \(x=3\), \(\dfrac{dy}{dx}=\dfrac{9}{2}\)
del gráfico: pendiente de la línea tangente \(=\dfrac{9}{2}=4.5\). Coinciden.
Ejercicio 10.2. Encuentre cuál será la pendiente de la curva \[y = 0.12x^3 - 2,\] en el punto particular con \(x=2\).
Respuesta
\(1.44\).
Solución
\[\begin{align} & y=0.12 x^{3}-2 \\ & \frac{d y}{d x}=3 \times 0.12 x^{2}=0.36 x^{2} \end{align}\]
Cuando \(x=2, \quad \dfrac{d y}{d x}=1.44\).
Por lo tanto, la pendiente de la curva en el punto con \(x=2\) es \(1.44\).
Ejercicio 10.3. Si \(y = (x - a)(x - b)\), demuestre que en el punto particular de la curva donde \(\dfrac{dy}{dx} = 0\), \(x\) tendrá el valor \(\frac{1}{2} (a + b)\).
Solución
\[y=(x-a)(x-b)\] Usando la regla del producto: \[\begin{align} \frac{d y}{d x}&=(x-b)+(x-a)\\ &=2 x-a-b \end{align}\] Estableciendo \(\dfrac{dy}{dx}=0\), obtenemos \[x=\frac{a+b}{2}.\]
Ejercicio 10.4. Encuentre el \(\dfrac{dy}{dx}\) de la ecuación \(y = x^3 + 3x\); y calcule los valores numéricos de \(\dfrac{dy}{dx}\) para los puntos correspondientes a \(x = 0\), \(x = \frac{1}{2}\), \(x = 1\), \(x = 2\).
Respuesta
\(\dfrac{dy}{dx} = 3x^2 + 3\); y los valores numéricos son: \(3\), \(3 \frac{3}{4}\), \(6\), y \(15\).
Solución
\[\begin{align} & y=x^{3}+3 x \\ & \frac{d y}{d x}=3 x^{2}+3 \end{align}\]
Cuando \(x=0\), \(\dfrac{dy}{dx}=3\).
Cuando \(x=0\), \(\dfrac{dy}{dx}=3+\frac{3}{4}=3\frac{3}{4}=3.75\).
Cuando \(x=1\), \(\dfrac{dy}{dx}=6\).
Cuando \(x=2\), \(\dfrac{dy}{dx}=15\).
Ejercicio 10.5. En la curva cuya ecuación es \(x^2 + y^2 = 4\), encuentre los valores de \(x\) en esos puntos donde la pendiente \({} = 1\).
Respuesta
\(\pm \sqrt{2}\).
Solución
\[x^{2}+y^{2}=4\] Resolviendo para \(y\): \[y= \pm \sqrt{4-x^{2}}= \pm\left(4-x^{2}\right)^{\frac{1}{2}}\]
Para encontrar \(\dfrac{dy}{dx}\), sea \(u=4-x^{2}\). Entonces \(y= \pm u^{\frac{1}{2}}\) y
\[\begin{align} \frac{d y}{d x} & =\frac{d y}{d u} \cdot \frac{d u}{d x} \\ & = \pm \frac{1}{2} u^{-\frac{1}{2}}(-2 x) \\ & = \pm \frac{-x}{\sqrt{4-x^{2}}}=\mp \frac{x}{\sqrt{4-x^{2}}} \\ \frac{d y}{d x} & =1 \Rightarrow \mp \frac{x}{\sqrt{4-x^{2}}}=1 \end{align}\]
Primero consideremos el signo \(-\):
\[-x=\sqrt{4-x^{2}}\]
Debemos tener \(x \leq 0\) porque el lado derecho es no negativo.
\[\begin{align} & x^{2}=4-x^{2} \\ & 2 x^{2}=4 \\ & x= \pm \sqrt{2} \end{align}\] Solo \(x=-\sqrt{2}\) es aceptable.
Cuando \(x=-\sqrt{2}\):
\[y=+\sqrt{4-x^{2}}=+\sqrt{2}\]
Ahora consideremos el signo \(+\):
\[x=\sqrt{4-x^{2}}\] Debemos tener \(x \geq 0\) porque el lado derecho siempre es no negativo
\[\begin{align} x^{2} & =4-x^{2} \\ 2 x^{2} & =4 \\ x & = \pm \sqrt{2} \end{align}\] Solo \(x=+\sqrt{2}\) es aceptable.
Cuando \(x=+\sqrt{2}\): \[y=-\sqrt{4-x^{2}}=-\sqrt{2}\]
Por lo tanto, en dos puntos \((-\sqrt{2},+\sqrt{2})\) y \((+\sqrt{2},-\sqrt{2})\), la pendiente de la curva es 1.
Ejercicio 10.6. Encuentre la pendiente, en cualquier punto, de la curva cuya ecuación es \(\dfrac{x^2 }{3^2} + \dfrac{y^2}{2^2} = 1\); y dé el valor numérico de la pendiente en el lugar donde \(x = 0\), y en el donde \(x = 1\).
Respuesta
\(\dfrac{dy}{dx} = - \dfrac{4}{9} \dfrac{x}{y}\). La pendiente es cero donde \(x = 0\); y es \(\mp \dfrac{1}{3 \sqrt{2}}\) donde \(x = 1\).
Solución
\[\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\]
Método 1: Utilizando la regla de la cadena
\[\begin{align} & \frac{d\left(\frac{x^{2}}{9}\right)}{d x}+\frac{d\left(\frac{y^{2}}{4}\right)}{d x}=1 \\ & \frac{1}{9} 2 x+\frac{1}{4} 2 y \cdot \frac{d y}{d x}=0 \\ \end{align}\] Por lo tanto \[\frac{d y}{d x}=-\frac{\frac{1}{9} x}{\frac{y}{4}}=-\frac{4}{9} \frac{x}{y}\] o \[\begin{align} \frac{d y}{d x} & =-\frac{4}{9} \frac{x}{ \pm 2 \sqrt{1-\frac{x^{2}}{9}}} \\ & =\mp \frac{2}{3} \frac{x}{\sqrt{9-x^{2}}} \end{align}\]
Método 2: Podemos lograr el mismo resultado si resolvemos \[\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\] para \(y\). Es decir
\[\begin{align} y & = \pm 2 \sqrt{1-\frac{x^{2}}{9}} \\ & = \pm 2\left(1-\frac{x^{2}}{9}\right)^{\frac{1}{2}} \end{align}\]
Para encontrar \(\frac{d y}{d x}\), sea \(x=1-\frac{x^{2}}{9}\). Entonces \(y= \pm 2 u^{\frac{1}{2}}\) y \[\begin{align} \frac{d y}{d x} & =\frac{d y}{d u} \cdot \frac{d u}{d x} \\ & = \pm \frac{1}{2} u^{-\frac{1}{2}}\cdot(-2 x) \\ & = \pm \frac{-x}{\sqrt{4-x^2}}=\mp \frac{x}{\sqrt{4-x^2}} \end{align}\]
Cuando \(x=0, \quad \dfrac{d y}{d x}=0\)
Cuando \(x=1, \quad \dfrac{d y}{d x}=\mp \dfrac{2}{3 \sqrt{8}}=\mp \dfrac{1}{3 \sqrt{2}}.\) Para ser más específicos, cuando \(x=1\), si \(y>0\), entonces \(\dfrac{dy}{dx}=-\dfrac{1}{3\sqrt{2}}\), y si \(y<0\), entonces \(\dfrac{dy}{dx}=+\dfrac{1}{3\sqrt{2}}\).
Ejercicio 10.7. La ecuación de una tangente a la curva \(y = 5 - 2x + 0.5x^3\), siendo de la forma \(y = mx + n\), donde \(m\) y \(n\) son constantes, encuentre el valor de \(m\) y \(n\) si el punto donde la tangente toca la curva tiene \(x=2\) por abscisa.
Respuesta
\(m = 4\), \(n = -3\).
Solución
\[y=5-2 x+0.5 x^{3}\]
\[\frac{d y}{d x}=-2+1.5 x^{2}\]
Cuando \(x=2, \quad \frac{d y}{d x}=4\).
Cuando \(x=2, \quad y=5\).
La ecuación de la línea con pendiente 4 que pasa por \((2,5)\) es \[y-5=4(x-2)\] o \[y=4 x-3\] Por lo tanto,
\[m=4 \quad \text { y }\quad n=-3\]
Ejercicio 10.8. ¿A qué ángulo cortan dos curvas \[y = 3.5x^2 + 2 \quad \text{y} \quad y = x^2 - 5x + 9.5\] una a otra?2
Respuesta
Intersecciones en \(x = 1\), \(x = -3\). Ángulos \(153^\circ\;26'\), \(2^\circ\;28'\).
Solución
Primero, necesitamos calcular, en qué punto estas dos curvas se intersectan:
Igualando las ecuaciones de las dos curvas:
\[3.5 x^{2}+2=x^{2}-5 x+9.5\] \[\Rightarrow 2.5 x^{2}+5 x-7.5=0\] \[\begin{align} \Rightarrow \quad x&=\frac{-5 \pm \sqrt{25+4 \times 2.5 \times 7.5}}{5} \\ &=\frac{-5 \pm 10}{5} \end{align}\]
Por tanto, estas dos curvas se cortan en \(x=-3\) y \(x=1\).
Ahora necesitamos encontrar las pendientes de estas dos curvas en \(x=3\) y \(x=1\).
\[\begin{align} & y=3.5 x^{2}+2 \Rightarrow \frac{d y}{d x}=7 x \\ & y=x^{2}-5 x+9.5 \Rightarrow \frac{d y}{d x}=2 x-5 \end{align}\]
Cuando \(x=-3\), la pendiente de la primera curva es \(-21\) y la pendiente de la segunda curva es \(-11\).
Es decir, \(\tan \alpha=-21\) y \(\tan \beta=-11\), donde \(\alpha\) y \(\beta\) son los ángulos que sus tangentes forman con la dirección positiva del eje \(x\).
\[\begin{gathered} \tan \alpha=-21 \Rightarrow \alpha=\arctan (-21) \approx-1.52 ~\mathrm{rad} \\ \text { o }\quad \alpha \approx-87.27^{\circ} \\ \tan \beta=-11 \Rightarrow \beta=\arctan (-11) \approx-1.48~ \mathrm{rad}\\ \text { o }\quad \beta \approx-84.81^{\circ} \end{gathered}\] Por lo tanto, el ángulo entre ellas cuando \(x=3\) es \(87.27-84.81=2.47^{\circ}\) o
\[\text { ángulo }=2^{\circ}+0.47 \times 60^{\prime} \approx 2^{\circ} 28^{\prime}\]
De manera similar, cuando \(x=1\), la pendiente de la primera curva es \(7\). \[\tan \alpha=7 \Rightarrow \alpha=\arctan 7 \approx 1.429~\mathrm{rad}\] o \[\alpha \approx 81.87^\circ\]
La pendiente de la segunda curva es \(-3\). \[\tan \beta=-3 \Rightarrow \beta=\arctan (-3) \approx-1.249~\mathrm{rad}\] o \[\beta \approx-71.57^{\circ}\] Por tanto, el ángulo entre ellas cuando \(x=1\) es \(81.87+71.57=153.44\) o \[\text { ángulo }=153^{\circ}+0.44 \times 60^{\prime} \approx 153^{\circ} 26^{\prime}\]
Ejercicio 10.9. Tangentes a la curva \(y = \pm \sqrt{25-x^2}\) se dibujan en puntos para los cuales \(x = 3\) y \(x = 4\). Encuentre las coordenadas del punto de intersección de las tangentes y su inclinación mutua.
Respuesta
Intersección en \(x =\frac{25}{7}\approx 3.57\), \(y=\frac{25}{7}\approx 3.57\). Ángulo \(16^\circ\;16'\).
Solución
Consideremos \(y>0\). El caso donde \(y<0\) se puede obtener por simetría. \[\begin{align} y & =+\sqrt{25-x^{2}} \\ \frac{d y}{d x} & =\frac{-2 x}{2 \sqrt{25-x^{2}}}=\frac{-x}{\sqrt{25-x^{2}}} \end{align}\]
Cuando \(x=3, \quad \dfrac{d y}{d x}=\frac{-3}{4}\).
Cuando \(x=3,\quad y=4\).
La ecuación de la línea tangente en \(x=3\) y \(y>0\) es entonces \[y-4=-\frac{3}{4}(x-3)\] o \[y=-\frac{3}{4} x+\frac{25}{4}\]
Cuando \(x=4,\quad \dfrac{d y}{d x}=-\frac{4}{3}\).
Cuando \(x=4,\quad y=3\).
La ecuación de la línea tangente es
\[y-3=-\frac{4}{3}(x-4)\] o \[y=-\frac{4}{3} x+\frac{25}{3}\]
Para encontrar la intersección de las líneas tangentes en \(x=3\) y \(x=4\) (para \(y>0\)), establecemos las ecuaciones de estas dos líneas tangentes iguales:
\[\begin{align} -\frac{3}{4} x+\frac{25}{4} & =-\frac{4}{3} x+\frac{25}{3} \\ \Rightarrow\ \frac{7}{12} x & =\frac{25}{12} \\ \Rightarrow\ x & =\frac{25}{7} \approx 3.57 \end{align}\]
Cuando \(x=\frac{25}{7}, y=-\frac{3}{4} \times \frac{25}{7}+\frac{25}{4}=\frac{25}{7} \approx 3.57\). Por lo tanto, estas dos líneas tangentes se interceptan en el punto \((\frac{25}{7},\frac{25}{7})\approx (3.57, 3.57)\).
Dado que la pendiente de la primera línea tangente es \(-3/4\), la pendiente del ángulo que forma con el eje \(x\) positivo es \[\alpha=\arctan \left(-\frac{3}{4}\right) \approx-0.643 \text { rad }\] o \[\alpha \approx-36.87^{\circ}\] De manera similar, la pendiente de la segunda línea tangente es \(-\frac{4}{3}\) y, por lo tanto, el ángulo que forma con el eje \(x\) positivo es \[\beta=\arctan\left(-\frac{4}{3}\right)\approx -0.927~\text{rad}\] o